
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неявная функция двух переменных.
Уравнением Имеют место соотношения
Пример. Неявная функция двух переменных задана уравнением Решение. Имеем Теперь Задачи для контрольной работы Найти производную функции 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13.
2.3. Уравнение касательной плоскости и нормали. 2.3.1. Касательная плоскость к поверхности
2.3.2. Нормаль к поверхности
Пример. Составить уравнение касательной плоскости и нормали к поверхности Решение. Нам даны абсцисса
Теперь подставляем найденные значения в уравнение касательной плоскости:
Запишем также уравнение нормали: Задачи для контрольной работы Найти уравнение касательной плоскости и уравнение нормали к поверхности 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13.
Градиент и производная по направлению 2.4.1. Производная по направлению. Рассмотрим вектор
естественно рассматривать как скорость изменения функции в точке Производную по направлению можно вычислить следующим образом:
где 2.4.2. Градиент. Вектор, определяющий направление наискорейшего возрастания функции
Пример. Даны функция а) градиент данной функции в точке М; б) производную этой функции в точке Решение. Преобразуем данную функцию к виду
Теперь определяем градиент данной функции в точке
Для нахождения производной данной функции в точке М в направлении вектора
Теперь подставляя в формулу для производной по направлению найденные величины и ранее вычисленные значения частных производных в точке М, имеем
Ответ:
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.176.67 (0.01 с.) |
 задается зависимость переменной z от переменных x и y. Если эта зависимость
задается зависимость переменной z от переменных x и y. Если эта зависимость  - функциональная, то имеет смысл ставить вопрос о вычислении частных производных
- функциональная, то имеет смысл ставить вопрос о вычислении частных производных 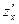 и
и 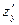 .
. ,
,  .
. . Найти
. Найти  . Найдем частные производные
. Найдем частные производные 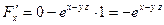 ,
,  ,
, 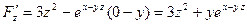 .
.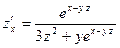 ,
,  .
.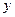 , заданной неявно уравнением.
, заданной неявно уравнением. . 14.
. 14. 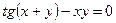 .
.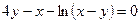 . 15.
. 15.  .
.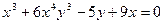 . 16.
. 16.  .
. . 17.
. 17. 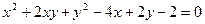 .
.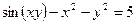 . 18.
. 18.  .
. . 19.
. 19. 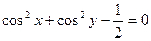 .
.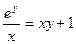 . 20.
. 20.  .
.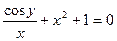 . 21.
. 21. 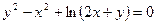 .
.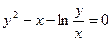 . 22.
. 22. 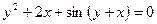 .
. . 23.
. 23. 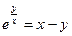 .
.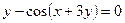 . 24.
. 24. 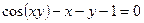 .
. . 25.
. 25.  .
.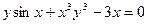 .
.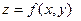 в точке
в точке 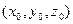 , где
, где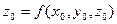 , имеет уравнение
, имеет уравнение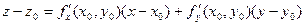 .
. в точке
в точке 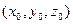 , где
, где  .
.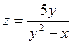 в точке с координатами
в точке с координатами 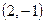 .
. и ордината
и ордината  точки касания, найдем аппликату этой точки:
точки касания, найдем аппликату этой точки: 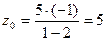 . Для составления искомых уравнений потребуются значения частных производных в точке касания
. Для составления искомых уравнений потребуются значения частных производных в точке касания
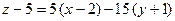 или
или 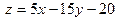 .
. .
.
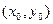
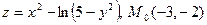 . 14.
. 14. 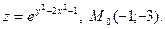
 . 15.
. 15. 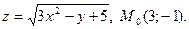
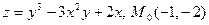 . 16.
. 16. 
 17.
17. 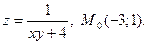
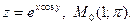 18.
18. 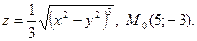
 19.
19. 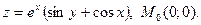
 20.
20. 
 21.
21. 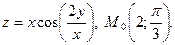
 22.
22. 
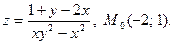 23.
23. 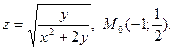
 24.
24. 
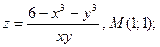 25.
25. 
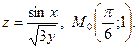
 , соединяющий точки
, соединяющий точки 
 и
и 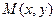 координатной плоскости. Предел вида
координатной плоскости. Предел вида
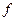 в точке
в точке 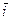 .
. =
=  ,
,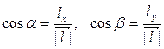 направляющие косинусы вектора
направляющие косинусы вектора 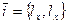 .
. Градиент имеет следующие координаты:
Градиент имеет следующие координаты: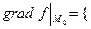
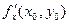 ,
,  и точка
и точка  . Найти:
. Найти: по направлению вектора
по направлению вектора 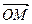 , где точка
, где точка  - начало координат.
- начало координат. и найдем ее частные производные в точке М:
и найдем ее частные производные в точке М: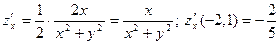 ,
,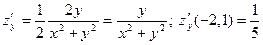 .
.
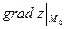
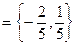 .
. найдем координаты вектора
найдем координаты вектора  , его модуль
, его модуль 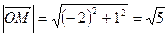 и его направляющие косинусы
и его направляющие косинусы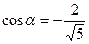 ,
, 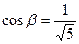 .
. .
.



