
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции одной переменнойСтр 1 из 4Следующая ⇒
1.1.1. Понятие предела – одно из основных в математическом анализе. Не приводя строгих определений, объясним смысл указанного понятия. Пусть дана функция
В случае, когда значения аргумента х неограниченно растут по модулю, оставаясь при этом положительными (отрицательными), мы записываем Если в (любом из трех рассмотренных случаев) А= 0, то функция Возможен также случай, когда значения функции
а функцию Следует заметить, что если функция Если рассмотреть, в частности, функцию натурального аргумента (последовательность)
1.1.2. Всякая элементарная функция Этим свойством пользуются при вычислении пределов. Кроме того, при выполнении арифметических операций над функциями соответствующие операции выполняются и над их пределами. 1.1.3. Неопределенностями (при 1.1.4. Приемы вычисления пределов. Вычисление пределов рациональных или иррациональных дробей на бесконечности может быть произведено путем одновременного деления числителя и знаменателя на старшую степень аргумента, чем достигается переход от бесконечно больших к бесконечно малым. Продемонстрируем прием на следующем примере.
Пример. Вычислить Решение. Имеем бесконечно большие в числителе и знаменателе дроби; следовательно, выполняем одновременное деление на старшую степень аргумента, т.е. на
Теперь имеем бесконечно малую в знаменателе дробь и функцию, стремящуюся к
Пример. Вычислить Решение. Имеем неопределенность вида
так что искомый предел равен 0,5. 1.1.5. Замечательные пределы. 1) При 2) При Рассмотренные пределы называются, соответственно, первым и вторым замечательными пределами. Второй замечательный предел может быть также записан в равносильной форме
Пример. Вычислить a) Решение. а) Имеем неопределенность вида
и закончить вычисление:
б) Имеем «комбинированную» неопределенность вида
Теперь
Теперь, пользуясь свойством непрерывности показательно-степенной функции, перейдем по-отдельности к пределу в основании и показателе степени:
Имеем в) Непосредственная подстановка значения
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.85.76 (0.009 с.) |
 и значения аргумента х неограниченно приближаются к значению
и значения аргумента х неограниченно приближаются к значению  , но не совпадают с
, но не совпадают с  ). Если при этом оказывается, что значения
). Если при этом оказывается, что значения  в точке
в точке 
 .
. (
( ). Если не принципиально, какого знака значения аргумента х, то употребляем символ
). Если не принципиально, какого знака значения аргумента х, то употребляем символ  Запись
Запись  означает, что значения
означает, что значения  называется бесконечно малой.
называется бесконечно малой. или -
или -  ) при стремлении аргумента х к некоторому
) при стремлении аргумента х к некоторому  и
и 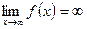 ,
, соответственно).
соответственно). бесконечно малая (бесконечно большая).
бесконечно малая (бесконечно большая). , то к ней применимо определение предела на бесконечности; используют запись
, то к ней применимо определение предела на бесконечности; используют запись .
. непрерывна на своей области определения
непрерывна на своей области определения  . Это означает возможность перехода к пределу под знаком функции
. Это означает возможность перехода к пределу под знаком функции  :
:  .
. или
или  ,
,  и др.
и др. .
.
 =
= 
 в числителе, т.е. дробь оказывается бесконечно большой. Ответ записываем в виде
в числителе, т.е. дробь оказывается бесконечно большой. Ответ записываем в виде .
. .
. . Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, т.е. на
. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, т.е. на 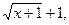 и сократим числитель и знаменатель на общий множитель х, (который при
и сократим числитель и знаменатель на общий множитель х, (который при  не равен нулю). В результате имеем
не равен нулю). В результате имеем
 отношение
отношение  представляет собою неопределенность вида
представляет собою неопределенность вида  . Можно доказать, что
. Можно доказать, что  .
. представляет собою неопределенность вида
представляет собою неопределенность вида  . Можно доказать, что соответствующий предел существует и равен некоторому иррациональному числу е =2,7…:
. Можно доказать, что соответствующий предел существует и равен некоторому иррациональному числу е =2,7…:  .
. .
. , б)
, б)  , в)
, в) 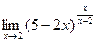 .
. (см. первый замечательный предел) отношение
(см. первый замечательный предел) отношение  (вместе с
(вместе с  ) стремится к единице. При вычислении предела отношения
) стремится к единице. При вычислении предела отношения  можно снова воспользоваться первым замечательным пределом, если положить
можно снова воспользоваться первым замечательным пределом, если положить  и заметить, что
и заметить, что  при
при  . Остается выполнить преобразование
. Остается выполнить преобразование =
= 


 . Если выделить в скобках в качестве слагаемого число 1, то станет возможным использование второго замечательного предела:
. Если выделить в скобках в качестве слагаемого число 1, то станет возможным использование второго замечательного предела: .
. при
при  , поэтому в показателе степени удобно выделить выражение вида
, поэтому в показателе степени удобно выделить выражение вида  , т.е.
, т.е.  :
: .
. (второй замечательный предел при
(второй замечательный предел при  ),
), 
 .
. приводит к неопределенному выражению вида
приводит к неопределенному выражению вида  . Снова используем прием выделения слагаемого, равного 1:
. Снова используем прием выделения слагаемого, равного 1: =
= 



