
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффицента трения скольжения 44м.
1. Рассказать о видах трения: трении покоя, внешнем и внутреннем трении, сухом и жидкостном трении, трении скольжения и трении качения. 2. Природа сил трения. Сущность молекулярно-механической теории трения. 3. Продемонстрировать знание законов сухого трения. Закон трения скольжения (закон Амонтона). Более точный закон трения скольжения (при скольжении по очень гладкой поверхности). Приближенный закон Кулона для вычисления силы трения качения. 4. Объяснить методику определения коэффициента трения скольжения в данной работе. 5. Решить задачу. Пример. Определить ускорение тела, соскальзывающего с наклонной плоскости, если угол наклона плоскости a =30°, а коэффициент трения между телом и наклонной плоскостью 0,3.
a =30° Эта задача на II закон Ньютона, алгоритм решения таких задач известен: μ = 0,3 1. Расставим силы, действующие на тело:
а -?
2. Запишем II закон Ньютона в векторном виде:
3. Запишем это уравнение в скалярном виде, спроецировав все векторные величины на выбранные оси. Ось x направим вдоль наклонной плоскости, а ось y – перпендикулярно ей. OX) mg sin α - Fтр = mа (1) OY) – mg cos α + N = 0 (2) Учтем, что Fтр = μ·N (3) Перепишем уравнения (1) и (2) в следующем виде с учетом (3): mg sin α − μ·N = mа mg cos α = N Подствавив одно уравнение в другое, получим: mg sin α − μ·mg cos α = mа Отсюда: α = sin α − μ cos α α = 0,24 м/с2. Ответ: α = 0,24 м/с2.
Определение модуля упругости методом растяжения 12м. 1. Кристаллические и аморфные тела. Их физические свойства. 2. Рассказать о видах деформации: упругой и пластической, о деформации при растяжении и сжатии твердого тела, сдвиге, изгибе, кручении. 3. Графическое изображение упругой и пластической деформации. Предел упругости, предел прочности. 4. Сила упругости. Записать закон Гука для пружины и стержня при продольном растяжении. 5. Привести формулы модуля Юнга и коэффициента Пуассона, объяснить, что характеризует данная величина. 6. Записать формулы работы и потенциальной энергии сжатой пружины.
Измерение момента инерции тел при помощи крестообразного маятника 8м. 1. Кинематика вращательного движения твердого тела: формулы по определению угловых величин − скорости, ускорения, перемещения. Связь угловых и линейных величин. Уравнения движения при равномерном, равноускоренном и равнозамедленном движении материальной точки по окружности.
2. Привести формулы по определению момента силы, момента инерции материальной точки и системы материальных точек, абсолютно твердого тела; назвать единицы измерения данных физических величин. 3. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси (вывод). 4. Уравнения моментов инерции тел правильной геометрической формы − стержня, кольца, цилиндра, шара для оси вращения, проходящей через центр масс тел. Привести пример вывода уравнения момента инерции для одного из перечисленных тел. 5. Теорема Штейнера и ее применение. Решить задачу по теме. Пример. Найти моменты инерции маховика в виде сплошного диска массой 0,5 кг и радиусом 50 см в трех случаях: 1) когда ось вращения проходит через центр масс диска; 2) когда ось вращения параллельна той, которая бы проходила через центр масс диска, но находится на расстоянии 20 см от него; 3) когда ось вращения проходит через точку лежащую на ободе маховика.
m = 0,5 кг В первом случае момент инерции находится по известной формуле: R = 0,5 м I = mR2/2 a2 = 0,2 м I = 0,5·(0,5)2/2 = 0,0625 кг·м2. a3 = 0,5 м Во втором случае применим теорему Штейнера:
а -? где Iс − момент инерции для оси вращения, проходящей через центр масс (мы его рассчитали в задании 1), a − расстояние от оси вращения до центра масс. I = 0,0625 + (0,5(0,2)2) = 0,0825 кг·м2. В третьем случае также применим теорему Штейнера, только расстояние от оси вращения до центра масс будет равно a3 = 0,5 м: I = 0,0625 + (0,5(0,5)2) = 0,1875 кг·м2. Ответ: I1 = 0,0625 кг·м2, I2 = 0,0825 кг·м2, I3 = 0,1875 кг·м2. Примечание: результаты можно округлять до сотых.
|
|||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 424; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.212 (0.004 с.) |
 Дано: Решение
Дано: Решение _______
_______  - сила притяжения;
- сила притяжения;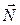 - сила нормальной реакции опоры;
- сила нормальной реакции опоры; - сила трения.
- сила трения.



