
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 7. Взаємозв'язки між групами: кореляційно-регресійний аналіз
Кореляційний аналіз Кореляційний аналіз – метод дослідження взаємозалежності ознак у генеральній сукупності, які є випадковими величинами з нормальним характером розподілу. Основними вимогами до застосування кореляційного аналізу є достатня кількість спостережень, сукупності факторних і результативних показників, а також їх кількісний вимір і відображення в інформаційних джерелах. Застосування кореляційного аналізу тісно пов'язане з регресійним аналізом, тому його часто називають кореляційно-регресійним. Головними завданнями кореляційного аналізу є: – визначення наявності та форми зв'язку; – вимірювання щільності (сили) зв'язку; – виявлення впливу факторів на результативну ознаку. Напрямок та сила взаємозв’язку між ознаками відображаються у математичному показнику, який називається коефіцієнтом кореляції r. Для оцінки лінійного зв’язку між двома кількісними ознаками з нормальним розподілом застосовують коефіцієнт кореляції Пірсона. У випадку асиметричного розподілу даних застосовується коефіцієнт рангової кореляції Спірмена. Його використовують також у тому випадку, коли між ознаками можливий нелінійний зв’язок. Проте в біохімічних та інших біологічних дослідженнях найчастіше використовують саме коефіцієнт кореляції Пірсона, який ми опишемо детальніше. В таблиці 23 та на рисунку 6 показано умовну відповідність між величиною коефіцієнту кореляції і тіснотою зв'язку (так звана «шкала Чеддока», складена американським математиком Робертом Е. Чеддоком). Як бачимо тільки при r=1 зв’язок між досліджуваними ознаками є функціональним, який описується лінійним рівнянням (див. рис. 6).
Таблиця 23. Величина коефіцієнту кореляції і тіснота зв'язку за «шкалою Чеддока»
В біології, а особливо, в медицині, умовно прийнято вважати наявність кореляційного взаємозв’язку між досліджуваними ознаками, тільки в тому випадку, коли коефіцієнт кореляції є не меншим за 0,7 (тобто «сильна» і «дуже сильна» кореляція за «шкалою Чеддока»).
Кореляційні зв'язки можна вивчати на якісному рівні з діаграм розсіяння емпіричних значень змінних X і Y (рис. 6) і відповідним чином їх інтерпретувати. Так, наприклад, якщо підвищення рівня однієї змінної супроводжується підвищенням рівня іншої, то йдеться про позитивну кореляцію або прямий зв'язок ( Коефіцієнт кореляції r для вибірки є точковою оцінкою генерального коефіцієнту кореляції – параметру ρ. Як для будь-якої випадкової величини, значення r може змінюватись при повторних дослідженнях вибірок, взятих з тієї самої генеральної сукупності. Тому коефіцієнт кореляції для вибірки має статистичну помилку, яку можна обчислити за формулою:
де sr – статистична помилка вибіркового коефіцієнту кореляції, r – вибірковий коефіцієнт кореляції, n – число вивчених об’єктів, в яких поміряні дві ознаки. Довірчий інтервал для коефіцієнту кореляції двох ознак, які розподіляються нормально буде охоплювати: r – tsr ≤ ρ ≤ r + tsr (70), де r – tsr – нижня, r + tsr – верхня межа довірчого інтервалу. При аналізі зв’язку перевіряється нульова гіпотеза: в генеральній сукупності зв’язок між ознаками відсутній (Н0: ρ = 0). При нормальному розподілі обох ознак, для перевірки нульової гіпотези використовують критерій Стьюдента t: t = r / sr, де r – коефіцієнт кореляції, sr – статистична помилка коефіцієнта кореляції. Розрахований критерій порівнюють з табличним при числі ступенів свободи df = n – 2.
Рис 6. Діаграми розсіяння емпіричних значень змінних X і У: а) зв’язок описується рівнянням y=ax+b, де a – ордината у точці перетину лінії регресії з віссю ординат, а b – тангенс кута нахилу лінії регресії до вісі абсцис; б) сильна позитивна кореляція; в) нульова кореляція (кореляція відсутня); г) помірна негативна кореляція; ґ) зв’язок описується рівнянням y=ax+b; д) нелінійна кореляція.
Основними етапами кореляційного аналізу є наступні: 1. Оформляємо отримані нами дані за двома ознаками у вигляді таблиці:
2. Підставимо отримані дані з вказаної вище таблиці в наступну формулу:
3. Отримавши коефіцієнт кореляції r перевіряємо його статистичну значущість за допомогою t критерію Стьюдента. При цьому висувається гіпотеза про те, що r=0:
Якщо обчислене значення tp>tкр (таблиця 1) при рівні статистичної значущості p<0,05 і певному числі ступенів свободи (df=n-2), то гіпотеза про відсутність зв’язків між ознаками (r=0) відкидається. 4. Беручи до уваги результати обчислень із таблиці, враховуючи знак коефіцієнта кореляції та тісноту зв’язку за таблицею 23, можна говорити про взаємозв’язки між досліджуваними ознаками. 5. Для лінійної залежності коефіцієнт детермінації рівний квадрату коефіцієнту кореляції: R2=r2 (73), де r – коефіцієнт кореляції. Даний показник вказує наскільки зміни величини Х приводять до змін величини У. Так, при r = 0,9 близько 81% (0,92 × 100% ≈ 81%) змін однієї ознаки визначається змінами іншої, в 19% випадків співпадіння чи неспівпадіння варіацій двох ознак є чисто випадковими. Приклад 26. За наведеними даними потрібно вказати на наявність чи відсутність взаємозв’язків між активністю лактатдегідрогенази (Xi) та вмістом лактату (Уі) в плазмі крові карася сріблястого: Xi: 6,28; 6,89; 7,34; 7,92; 8,26; 8,74; 8,39; 8,34; 8,74; 9,72; 14,0; 15,6; 17,7; 18,5; 20,1; 22,9; 24,8; 31,3; 36,2; 39,9. Yi: 5,11; 5,82; 6,96; 7,39; 7,07; 7,73; 7,81; 7,56; 8,00; 8,45; 8,77; 9,01; 9,13; 9,45; 9,77; 10,1; 10,6; 10,8; 11,3; 12,4. 1. Оформляємо отримані нами дані за двома ознаками у вигляді таблиці:
2. Обчислюємо коефіцієнт кореляції за формулою (71):
3. За формулою (72) перевіряємо статистичну значущість коефіцієнта кореляції r за допомогою t критерію Стьюдента:
Число ступенів свободи в даному випадку: df=n–2=20–2=28. Знаходимо t0,05 по таблиці 1 для визначення критерію Стьюдента. Умова tr>t0,05, оскільки 10,73>2,10. Тому між даними спостерігається дуже сильна позитивна кореляція, достовірна при рівні статистичної значущості p<0,05. 4. Обчислюємо за формулою (73) коефіцієнт детермінації: R2=0,932=0,86 Отже, за результатами кореляційного аналізу можна зробити висновок про те, що взаємозв’язок між активністю лактатдегідрогенази і вмістом лактату за напрямком – пряма, за тіснотою (таблиця 23) – дуже сильна, проте наочно за формою графіка важко визначити форму цієї залежності (див. рис. 7).
Рис. 7. Кореляційне поле залежності активності лактатдегідрогенази і вмісту лактату в плазмі крові карася сріблястого
Тому в наступному підрозділі визначимо вид регресії, яка найбільш адекватно описує цю залежність.
Парний регресійний аналіз Коефіцієнт кореляції вказує лишень на ступінь зв’язку у варіації двох змінних величин. Проте він не дає змогу судити про те, як кількісно змінюється одна величина при зміні іншої. Для цього існує інший метод – це метод регресії. Цей аналіз можна використовувати для виявлення взаємозв’язку між фактором, що впливає на об’єкт (Х), і параметром, що змінюється (У). Розрізняють лінійні і нелінійні регресії. Рівняння лінійної парної регресії наступне:
де у – значення параметру Y; а – вільний член; b – коефіцієнт регресії; х – незалежна змінна;
При центрованості помилок
де Коефіцієнт регресії b обчислюють за формулами (76) або (77):
Нелінійний взаємозв’язок між даними може описуватись різними функціями: Гіперболічною: Показниковою: Напівлогарифмічною: Логарифмічною: Степеневою: Е кспоненційною: Зворотньою: Параболічною (Поліноміальна модель другого порядку): y = ax2 + bx + c (85); Кубічною (Поліноміальна модель третього порядку): y = ax3 + bx2 + cx + d (86)
і поліноміальними моделями вищих порядків.
Часто перед дослідниками постає ряд питань, а саме: яке рівняння регресії використати для опису своїх даних, яке з них найбільш адекватно описує дані з найменшими похибками і помилками та ін.? Тому в даній роботі ми зупинимось на обчисленні коефіцієнтів a і b для різних рівнянь, порівнянні рівнянь між собою, виборі оптимального виду рівняння регресії, обчисленні похибок та помилок цих рівнянь. Вирішення завдання побудови якісного рівняння регресії, що відповідає емпіричним даним і меті дослідження, є достатньо складним і багатоступеневим процесом. Його можна розбити на три етапи: 1) вибір формули рівняння регресії; 2) визначення параметрів вибраного рівняння; 3) аналіз якості рівняння і перевірка його адекватності емпіричним даним. Вибір формули, зазвичай, здійснюється за графіком реальних статистичних даних у вигляді точок в декартовій системі координат (діаграма розсіювання). Проте нерідко виникають ситуації, коли розміщення точок приблизно відповідає декільком функціям і необхідно вибрати з них найкращу. На практиці невідомо, яка модель вірна, і часто підбирають таку модель, яка найбільше відповідає реальним даним. Ознаками «доброї» моделі є:
1. Простота. Модель повинна бути максимально простою. Дана властивість визначається тим фактом, що модель не відображає дійсність ідеально, а є її спрощенням. 2. Максимальна відповідність. Рівняння тим краще, чим більшу частину діапазону залежної змінної воно може пояснити. 3. Прогнозні якості. Модель може бути визнана якісною, якщо отримані на її основі прогнози підтверджуються реальністю. Для обчислення коефіцієнтів регресійних рівнянь рекомендується використовувати метод найменших квадратів (МНК), який був запропонований на початку ХІХ ст. Лежандром і Гауссом. Вимога МНК заключається в тому, що теоретичні дані лінії регресії у повинні бути отримані таким чином, щоб сума квадратів відхилень від цих даних емпіричних величин даних була мінімальною, тобто: Σ(Yi – Yx)2 → min (87) Основні етапи обчислень: 1. Знаходимокоефіцієнти рівнянь регресії 1.1. Рівняння лінійної регресії Для обчислення коефіцієнтів a і b рівняння лінійної регресії (74) необхідно розв’язати нормальні рівняння методу найменших квадратів:
Із цієї системи можна знайти коефіцієнти а і b: a = (Σ yi Σ(xi)2 – Σ yi xi Σ xi)/(n Σ(xi)2 – (Σ xi)2) (89) , b = (n Σ yi xi – Σ xi Σ yi) / (n Σ(xi)2 – (Σ xi)2) (90) . 1.2. Лінійне рівняння з логарифмуванням факторної ознаки (напівлогарифмічне) Для обчислення коефіцієнтів a і b рівняння прямої з логарифмуванням факторної ознаки (80) необхідно розв’язати наступну систему рівнянь:
Із цієї системи можна знайти коефіцієнти а і b: a = (Σ yi Σ(ln xi)2 – Σ yi ln xi Σ ln xi)/(n Σ(ln xi)2 – (Σ ln xi)2 ) (92), b = (n Σ yi ln xi – Σ ln xi Σ yi) / (n Σ(ln xi)2 – (Σ ln xi)2 (93). 1.3. Лінійне рівняння з логарифмуванням ознак (логарифмічне) Для обчислення коефіцієнтів a і b рівняння прямої з логарифмуванням факторної ознаки (81) необхідно розв’язати наступну систему рівнянь:
Із цієї системи можна знайти коефіцієнти а і b: a = (Σ lnyi Σ(ln xi)2 – Σ lnyi ln xi Σ ln xi)/(n Σ(ln xi)2 – (Σ ln xi)2 ) (95), b = (n Σln yi ln xi – Σ ln xi Σln yi) / (n Σ(ln xi)2 – (Σ ln xi)2 (96). 1.4. Рівняння гіперболічної регресії Нормальні рівняння методу найменших квадратів для гіперболи (78) такі:
Результатом обчислення системи нормальних рівнянь є наступні рівняння: a = (Σ yi Σ(1/xi) 2 – Σ(yi / xi) Σ(1/xi)) / n Σ(1/xi) 2- (Σ(1/xi))2 (98), b = n Σ(yi / xi) - Σ(1/xi) Σ yi / n Σ(1/xi) 2- (Σ(1/xi))2 (99). 1.5. Рівняння показникової кривої Для обчислення коефіцієнтів a і b рівняння (79) необхідно розв’язати наступну систему рівнянь:
Із цієї системи можна знайти коефіцієнти а і b: ln a = (Σ ln yi Σ xi2 – Σ xi ln yi Σ xi) / (n Σ xi2 – (Σ xi)2) (101), ln b = (n Σ xi ln yi–Σ xi Σ ln yi) / (n Σ xi2 – (Σ xi)2) (102). 1.6. Рівняння параболічної регресії
Для обчислення коефіцієнтів a, b і с рівняння (85) необхідно розв’язати наступну систему рівнянь:
2. Перевірку значущості параметрів рівняння регресії в цілому проводимо на основі обчислень величини середньої помилки апроксимації
де yi – емпіричне значення результативної ознаки (результативною називається ознака, яка змінюється під впливом факторної ознаки); yx – теоретичне значення результативної ознаки. Значення середньої помилки апроксимації не має перевищувати 10-15%. 3. Перевірку адекватності регресійної моделі можна провести за допомогою кореляційного аналізу. Тісноту кореляційного зв’язку між x і y визначається за допомогою теоретичного кореляційного відношення (індекс кореляції) з рівнянь (105) або (106):
Підкореневий вираз – коефіцієнт детермінації (відповідно до формули (73) його значення під час обчислень потрібно помножити на 100%) – показує долю варіації результативної ознаки (у) під впливом варіації ознаки-фактору (х). Теоретичне кореляційне відношення може знаходитися в межах від 0 до 1. Чим ближче кореляційне відношення до 1, тим тісніший зв’язок між ознаками. 4. Коли декілька рівнянь адекватно прогнозують значення, то в такому випадку найбільш підходящим рівнянням регресії є те, яке характеризується найбільшим фактичним значенням F-критерію Фішера, який обчислюють за формулою: F ф = S y2 / S 2зал (107), де S y2 = (Σyi2 – ((Σyi)2 / n)) / n – 1 (108), S 2зал = Σ(yi – yx)2/ (n – 2) (109). 5. Обчислюємо похибки і помилки, оскільки, чим менші величини похибок і помилок, тим надійніше рівняння описує досліджуваний взаємозв'язок. Абсолютну похибку рівнянь (δ) обчислюємо за формулою:
Відносну похибку рівнянь (Δ) знаходимо за формулою:
Також обчислюємо систематичну (op) і випадкову помилки (oδ): op = (1/n)Σ((yi – yx)/yx) × 100 (112),
6. На основі фактичних значень F -критерію Фішера, похибок та помилок робимо загальний висновок про адекватність того чи іншого рівняння регресії. Приклад 27. За наведеними даними (приклад 26) потрібно встановити: форму зв’язку між активністю лактатдегідрогенази (Xi) та вмістом лактату (Уі) в плазмі крові карася сріблястого, параметри рівняння регресії та тісноту взаємозв’язку. 1. За методом найменших квадратів знаходимо коефіцієнти а і b вірогідних типів рівнянь регресії, будуємо графіки рівнянь регресії та здійснюємо перевірку значущості рівняння регресії. Рівняння лінійної регресії 1.1.1. Формуємо таблицю з первинних даних та обчислень допоміжних величин для обчислення коефіцієнтів a і b даного рівняння:
За допомогою вказаної вище таблиці та формул (89) і (90) отримуємо коефіцієнти регресії: a = 5,9791, b = 0,1668. Тоді рівняння регресії матиме наступний вигляд: y = 0,167 x + 5,979 1.1.2. За формулою (104) обчислюємо величину середньої помилки апроксимації
Отже, апроксимація даних наведеним вище рівнянням регресії є статистично значущою, оскільки 6,89 < 15%. 1.1.3. За допомогою формул (106) і (73) обчислюємо величини індексу кореляції та коефіцієнту детермінації:
R2=0,932 ×100% =86% 1.1.4 За формулою (107) обчислюємо фактичне значення F-критерію Фішера. При цьому порівнюємо загальну дисперсію Sy2 (108) із залишковою S2зал (109). S y2 = (1565,0– 1500,43) / 19 = 3,3984. S 2зал = 8,708 / 18 = 0,4838, Тоді за формулою (107): F ф = 3,3984 / 0,4838 = 7,02.
Рис. 8. Лінійна регресія
При рівні статистичної значущості Р=0,05 Fф>Fкр =2,22. Тому лінійне рівняння регресії адекватно описує фактичний взаємозв’язок між вмістом лактату і активністю ЛДГ. При цьому значення Fф=7,02 вказує на те, що рівняння лінії в сім разів краще описує даний взаємозв’язок, ніж середнє значення залежної змінної. Отже, за результатами регресійного аналізу можна зробити висновок про те, що отримане лінійне рівняння, якеза експериментальними даними має вигляд: y = 0,167 x + 5,979 (Рис. 8: пряма лінія) в 7,02 рази краще описує зміни залежної змінної (вміст лактату), ніж середнє значення аргументу.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 877; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.13.201 (0.11 с.) |
 рис. 6а, б). Якщо ж зростання однієї змінної супроводжується зниженням значень іншої, то маємо справу з негативною кореляцією або зворотним зв'язком (
рис. 6а, б). Якщо ж зростання однієї змінної супроводжується зниженням значень іншої, то маємо справу з негативною кореляцією або зворотним зв'язком ( рис. 6г, ґ). Нульовою називається кореляція за відсутності зв'язку між змінними (
рис. 6г, ґ). Нульовою називається кореляція за відсутності зв'язку між змінними ( рис. 6в). Проте нульова загальна кореляція може свідчити лише про відсутність лінійної залежності, а не взагалі про відсутність будь якого статистичного зв'язку.
рис. 6в). Проте нульова загальна кореляція може свідчити лише про відсутність лінійної залежності, а не взагалі про відсутність будь якого статистичного зв'язку. (69),
(69),

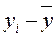

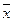

 (71)
(71) (72)
(72)
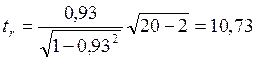

 (74),
(74), – помилка апроксимації.
– помилка апроксимації. (75),
(75), і
і  – середні значення фактору Х і параметру Y у вибірках з n спостережень.
– середні значення фактору Х і параметру Y у вибірках з n спостережень. (76)
(76) (77).
(77). (78);
(78); (79);
(79); (80);
(80); (81);
(81); (82);
(82); (83);
(83); (84);
(84);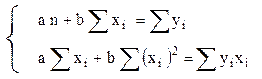 (88)
(88)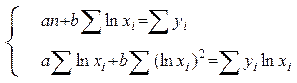 (91).
(91).  (94).
(94).  (97)
(97) (100)
(100)  (103)
(103)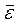 :
: (104)
(104) (105)
(105) (106)
(106)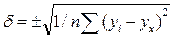 (110).
(110).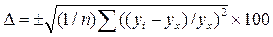 (111).
(111).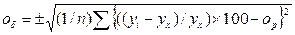 (113).
(113).





