
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 3. Похибки оцінювання параметрів вибірки
Помилка середньої арифметичної величини У розділі 2, ми моделювали варіацію зросту в дорослих людей. Крива, яка відобразила цю варіацію, задавалась функцією щільності нормального розподілу. В статистиці подібні функції використовується не тільки для опису варіації. У нашій моделі ми використовували групу з 992 особин. В окремих випадках, така велика група може бути генеральною сукупністю. Дослідник часто має справу з невеликою кількістю спостережень – вибіркою. Вибірка формується з генеральної сукупності шляхом випадкового відбору. У вказаному нами прикладі ми можемо відібрати декілька осіб зі зростом 182, 174, 155, 168, 176 та 194 см. Середнє значення для цієї вибірки дорівнюватиме приблизно 175 см, тоді як середнє для всієї сукупності було задане як 170 см. Візьмемо іншу вибірку зі значень, які утворюють криву на рис. 3 в розділі 2: наприклад, це індивідууми зі зростом 145, 163, 154, 174, 185 та 160 см. Середнє значення буде дорівнювати 163,5 см. Отже, ми бачимо, що обидві вибірки будуть по-різному представляти генеральну сукупність. Для встановлення тих меж, в яких знаходитиметься середнє арифметичне генеральної сукупності використовують стандартну помилку середньої арифметичної величини (англомовний термін – S.E.M., абревіатура від s tandard e rror of the m ean). Її можна обчислити за формулою:
Підставивши формулу (10) у формулу (14), отримаємо:
На відміну від стандартного відхилення s стандартна помилка середньої арифметичної величини m (її ще позначають як Приклад 11. Розрахуємо стандартну похибку середнього для наведених вище вибірок, взятих із сукупності осіб з різним зростом в межах від 145 до 200 см. Використавши формулу (15) для першої з наведених вище вибірок, отримаємо: Після заокруглення значень запис мав би виглядати наступним чином: 175 ± 5 та 164 ± 6. В обох випадках ми бачимо що середнє арифметичне значення для групи, з якої ми брали обидві вибірки, потрапляє в діапазон середнє арифметичне (для вибірки) ± похибка середнього. Так, середнє арифметичне для групи з 992 чоловік різного росту було задане як 170 см (див. Розділ 2). Для першої вибірки ми отримаємо це значення, якщо віднімемо стандартну похибку – 175 – 5 = 170. Для другої вибірки середнє значення для генеральної сукупності вийде при додаванні стандартної похибки – 164 + 6 = 170 см.
Довірчий інтервал Похибка репрезентативності середнього арифметичного вказує те, наскільки середнє арифметичне для вибірки близьке до середнього арифметичного для генеральної сукупності. Часто інформативнішим показником є інтервал, в який потрапляє значення параметру розподілу (середнього арифметичного, дисперсії) із заданою ймовірністю – довірчий інтервал (Δ x). Так, у наведеному вище прикладі, де аналізувався зріст 992 осіб, крайні значення становили 145 та 200 см. Візьмемо ще одну випадкову вибірку із зазначених 992 осіб: люди зі зростом 163, 150, 146, 193, 177 та 191 см. Середнє арифметичне для цієї вибірки становитиме 170 см, стандартна похибка – близько 8 см, стандартне відхилення – близько 20 см. В діапазон 170±20 см попадає близько 96,6% значень, які використовуються у нашій моделі. Для дослідника часто достатньо знати інтервал, в який вкладається не менше як 95% значень генеральної сукупності. В окремих випадках важливо знати інтервал, в якому знаходиться не менше як 97,5 або 99% значень. Відсоток граничних значень – 5, 2,5 або ж 1% називається рівнем значущості і позначається грецькою літерою α (або літерою p, якщо розраховується в долях одиниці). Існує також інше трактування рівня значущості, яке ми розглянемо в наступних розділах. Довірчий інтервал можна розрахувати, виходячи з функції розподілу. Для розрахунку довірчого інтервалу використовують не заданий, як на рисунку 3 (розділ 2), розподіл, а ідеалізований, в якому середнє значення дорівнює 0, а сам графік функції стає симетричним до осі ординат, на якій відкладається ймовірність випадкової події. Одиниці, які відкладаються на осі абсцис – стандартне відхилення – одне, два, три і так далі (рис. 4).
Рис. 4. Графік нормального розподілу даних
Графік, зображений на рисунку 4, показує ймовірність (у долях одиниці) потрапляння у вибірку значень, які відхиляються від середнього на n -ну кількість стандартних відхилень. Варто зазначити, що на рисунках 2 та 3 показана крива нормального розподілу, яка в обох випадках задається функцією (13), наведеною в розділі 2. Для того, щоб отримати графік на рисунку 3, ми задали 170 (см) як середнє та 10 (см) – стандартне відхилення. Додатково ми помножили кожну з отриманих ймовірностей на кількість осіб – 992. Графік на рисунку 3 являє собою криву нормального розподілу для випадку, коли середнє арифметичне дорівнює 0, а стандартне відхилення – 1. Підраховано, що при такому розподілі 95% значень будуть знаходитись в діапазоні середнє арифметичне ± 1,96 стандартних відхилень, або інакше μ ± 1,96· σ. Довірчий інтервал для середнього значення нормально розподіленої сукупності з відомою дисперсією σ можна розрахувати наступним чином:
Δ x = Саме за такою схемою розраховується довірчий інтервал програмою Microsoft Excel. Проте, цей спосіб розрахунку пасує тільки для великих вибірок. Тому для точнішого розрахунку довірчого інтервалу для невеликої вибірки (n < 30) використовують розподіл Стьюдента і значення t, які будуть обмежувати інтервал, куди потрапляє 95, 97,5 або ж 99% всіх значень генеральної сукупності. Тоді величину
де m – похибка середньої арифметичної величини; Число ступенів свободи (часто позначається, як df – d egrees of f reedom) дорівнюватиме n – 1, де n – розмір вибірки. Таблиця 1. Значення t при рівні статистичної значущості (p)
При розрахунку довірчого інтервалу ми також маємо бути впевнені, що дані, які аналізуються, підпорядковуються нормальному розподілу, як наприклад дані у використовуваному нами прикладі щодо зросту 992 осіб. Якщо дані не підпорядковуються нормальному розподілу (наприклад, смертність організмів, плодючість, кількісні характеристики поведінкових реакцій), то для оцінки вибірки розраховують медіану, квартилі, а також процентилі, які відповідають 99% та 1% значень. Приклад 12. Розрахуємо
Отже, в результаті обчислень ми отримали наступне значення активності ферменту:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.224 (0.007 с.) |
 (14).
(14). (15).
(15). ) не є характеристикою, що описує варіабельність ознаки у вибірці. Натомість, стандартна помилка вказує на точність, з якою показник вибірки – середнє арифметичне – представляє (репрезентує) середнє арифметичне для генеральної сукупності.
) не є характеристикою, що описує варіабельність ознаки у вибірці. Натомість, стандартна помилка вказує на точність, з якою показник вибірки – середнє арифметичне – представляє (репрезентує) середнє арифметичне для генеральної сукупності. ≈ 5,36, для другої відповідно ≈ 5,82.
≈ 5,36, для другої відповідно ≈ 5,82.
 ± 1,96· σ /
± 1,96· σ /  (16)
(16)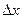 знаходимо за формулою:
знаходимо за формулою: (17),
(17), – коефіцієнт Стьюдента, значення якого залежатиме від числа ступенів свободи df = n – 1 розподілу Стьюдента. Інакше кажучи,
– коефіцієнт Стьюдента, значення якого залежатиме від числа ступенів свободи df = n – 1 розподілу Стьюдента. Інакше кажучи,  розподілу Стьюдента з df ступенями свободи. Значення коефіцієнту Стьюдента для деяких значень p і df наведені в таблиці 1.
розподілу Стьюдента з df ступенями свободи. Значення коефіцієнту Стьюдента для деяких значень p і df наведені в таблиці 1. і
і  для даних з активності супероксиддисмутази в печінці карася сріблястого – 154, 153, 125, 136, 142 і 146 Од/мг білка. Для цього використаємо формули (2), (15) і (17):
для даних з активності супероксиддисмутази в печінці карася сріблястого – 154, 153, 125, 136, 142 і 146 Од/мг білка. Для цього використаємо формули (2), (15) і (17): (Од./мг білка).
(Од./мг білка). (Од/мг білка).
(Од/мг білка). (Од/мг білка).
(Од/мг білка). (Од/мг білка).
(Од/мг білка).


