
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цель работы. Методом наименьших квадратов оценить коэффициенты линейной регрессии и провести проверку выполнения условий теоремы Гаусса-Маркова.Стр 1 из 5Следующая ⇒
Лабораторная работа № 1 «Парная регрессия» Цель работы. Методом наименьших квадратов оценить коэффициенты линейной регрессии и провести проверку выполнения условий теоремы Гаусса-Маркова.
Основная спецификация математической модели имеет вид:
Условия теоремы накладывают ограничения на случайную компоненту Математическое ожидание Ковариация соседних значений Дисперсия случайной компоненты D( Если эти условия выполняются, то оценки неизвестных коэффициентов Сам метод наименьших квадратов (МНК) и вычислительные формулы для расчета оценок коэффициентов приводятся в учебном пособии [1]. Здесь же следует пояснить следующее. Исходными для вычисления коэффициентов регрессии являются табличные значения пар чисел {(X1,Y1), (X2,Y2),…,(Xn,Yn). Из формулы (1) видно, что в ее правой части стоит случайная величина Оценивание коэффициентов регрессии. Функция ЛИНЕЙН. Табличный редактор EXCEL содержит добротный набор встроенных функций, облегчающих и ускоряющих процесс решения задач эконометрики. Приступая к лабораторной работе необходимо скопировать в свой файл таблицу исходных данных в соответствии с вариантом, заданным преподавателем. Исходные данные содержатся на листе «Исходные данные» файла «Парная регрессия 1» в папке «ЛабРаб».
Рис.1 Вариант В-1 и его размещение в окне процессора EXCEL приведен на рис. 1. Для статистических расчетов оценок коэффициентов регрессии и статистик, оценивающих результаты этих расчетов, воспользуемся функцией ЛИНЕЙН. Но прежде чем обратиться к этой функции необходимо подготовить место на листе EXCEL для вывода результатов расчета. При этом используется следующее правило: количество строк всегда равно 5; количество столбцов равно числу k+1, где k равно числу независимых (экзогенных) переменных. В случае парной регрессии k=1 и число столбцов равно 2. Для поиска функции ЛИНЕЙН необходимо выполнить одно из следующих действий: нажать клавиши <Shift>-<F3>; задать команду ФУНКЦИЯ из меню ВСТАВКА; нажать кнопку [fx] на стандартной панели. В ответ на это действие появится диалоговое окно выбора типа функции:
Рис.2 В окне «Категория» щелкнем левой клавишей мышки, в результате чего окно раскроется:
Рис.3 В раскрывшемся окне выделим категорию функций «Статистические» и прокруткой справа найдем в окне «Выберите функцию» функцию ЛИНЕЙН:
Рис.4 Щелкнув мышкой на клавише «ОК» получим следующий результат:
Рис.5 На этом рисунке слева вверху виднеется часть таблицы Вашего варианта расчета, ниже занимает почти всю площадь окна диалоговое окно, все 4 окошечка которого предстоит заполнить, а справа в ячейках (J3:K7) располагается выделенное ранее место для регистрации результата расчетов. Окно «Аргументы функции» легко смещается с помощью мышки в пределах окна монитора, позволяя заполнять 2 верхних окошка y и x координатами соответствующих массивов из таблицы исходных данных. В окошечки «Конст» и «Статистика» как правило заносятся единицы, что соответствует требованию рассчитывать оценки обоих коэффициентов регрессии
Рис.6 Далее нажимаем с помощью мышки клавишу «ОК» и большое окно приобретает вид:
Рис.7 Видно, что вычисления не заполняют выделенную справа таблицу - заполнена только одна ячейка с адресом J3. Чтобы заполнить эту таблицу полностью необходимо подвести курсор мышки в строку, где записана функция ЛИНЕЙН(С2:С13;В2:В13;1;1) и щелкнуть левой клавишей мышки. Окно EXCEL приобретет вид:
Рис.8 Теперь необходимо нажать одновременно клавиши <Ctrl>-<Shift>-<Enter> и результаты расчета заполнят таблицу справа полностью:
Рис.9 Рассмотрим подробнее информацию, полученную в результате обработки исходных данных функцией ЛИНЕЙН (рис.10).
Рис.10 Первая строка дает оценки коэффициентов регрессии и в соответствии с формулой (1) результат расчетов может быть записан так: Yt = 7,863 + 1,022*Xt + εt, где t = 1,2,…,12. Вторая строка несет информацию о разбросе случайных величин В третьей строке слева подсчитан коэффициент детерминации: R2 = 0,891. Это хорошее значение для коэффициента R2, который характеризует качество подгонки регрессии к значениям Yt. Наилучший вариант при R2 = 1 возник бы в том случае, если бы все значения Yt лежали на прямой подготовить (выделить) ячейку, куда будет записан результат; задать допустимый уровень значимости (допустимой вероятности ошибки) α, который, как правило, задается на уровне 5%, т.е. α = 0,05; указать число степеней свободы f1, равное числу независимых переменных k (в нашем случае k = 1); указать число степеней свободы f2 =n – (k+1). Эти данные содержатся в четвертой строке справа и f2 = 12 – (1+1) = 10.
Это значение получено после заполнения диалогового окна:
Рис.11 Далее производится сравнение критического значения со значением F-статистики. В нашем случае Построение графиков. Подготовим дополнительные даны для построения графиков. Для этого вычислим среднее значение
Рис.12 Нажимаем курсором на клавишу ОК и возникает диалоговое окно:
Рис.13 Рис.14 Для построения графиков необходимо обратиться к меню «Вставка» и выбрать в нем значение «Диаграмма» (см. рис. 15). После щелчка мышкой появится диалоговое окно
(см. рис.16).
Рис.15
Рис.16 Выделение показано на рис.16 (Тип «точечная» и вид – нижний левый рисунок). Нажимаем мышкой клавишу «Далее». Возникает диалоговое окно (рис.17), у которого два
Рис.17 Рис.18 В окне «Источник данных диа…» нужно заполнить три правых окошечка.
Рис.19 На рис.19 приведен фрагмент этапа работы с диаграммой, когда добавлены три ряда и диаграмма заполнена графиками. Следует сделать несколько замечаний. Рис.20 Окно на рис.20 заполняется названиями графиков и осей. После его заполнения нажимаем клавишу «Далее». Диалоговое окно на рис. 21 предлагает сделать выбор в размещении графика. После того, как он будет сделан, нажимаем клавишу «Готово».
Рис.21
Рис.22 Неприятное впечатление производит график «Знач. Y» соединительными линиями. Чтобы от них избавится, подведем курсор с помощью мыши точно на одну из соединительных линий и щелкнем левой клавишей мыши. Повторим щелчок правой клавишей – возникнет меню (см. рис. 23), в котором необходимо выбрать пункт 1: «Формат рядов данных».
Рис.23 Появится диалоговое окно, где в разделе «Линия» надо выбрать вариант «отсутствует».
Рис.24
Дисперсионный анализ Рис.30 Затем мышкой выделяем ячейку Е137, вводим с клавиатуры знак “-“, затем мышкой выделяем ячейку D137 и нажимаем <Enter>. В ячейке Е137 появляется результат. Ставим курсор в правый нижний угол ячейки, появляется крестик, который протягиваем до конца колонки.
Рис.31 Аналогично заносим в ячейку F137 формулу для вычисления выражения
Рис.32 Статистика DW служит инструментом для проверки гипотезы об отсутствии корреляции между соседними значениями последовательности случайных величин et. Для проверки гипотезы число DW размещается на одноименной оси рис.33 в соответствии со своим значением. Границами-ориентирами служат значения dl и du, определяемые по таблице в зависимости от числа наблюдений n в исходных данных и числа k – количества независимых переменных. Общая картина представлена на рис.33, частный случай представлен на рис.32.
Рис.33
Рис.34 Прежде всего выделяем таблицу исходных данных с помощью мышки, затем обращаемся к меню «Данные», где выделяем элемент меню «Сортировка» (см. рис.34). В ответ на это действие появляется диалоговое окно «Сортировка диапазона» (см. рис.35) выбирается Рис.35 Сортировка по возрастанию по столбцу Х. Важное условие такой сортировки – неразрывность пар (Xt,Yt), они могут перемещаться только вместе. В результате получаем новую таблицу, в верхней части которой сосредоточены меньшие значения Х, а в нижней – большие. При неравенстве дисперсий это неизбежно отразится на ESS в верхней и нижней части. Делим таблицу на две части поровну. Для каждой из частей определяем регрессию с помощью функции ЛИНЕЙН и выделяем значения ESS1 и ESS2 (см. рис. 36).
Рис.36 Вычисляем две статистики: статистку GQ=ESS1/ESS2 и 1/GQ=ESS2/ESS1. Затем по таблице или по функции Fраспробр определяем критическое значение F kr для уровня значимости α=0,05, числа степеней свободы для уравнения регрессии верхней половины таблицы (ячейка F5) и нижней половины (ячейка F11). Если обе статистики GQ<F kr и 1/GQ<F kr, то гипотеза о гомоскедастичности принимается с вероятностью 0,95. В противном случае, если хотя бы одно неравенство не выполняется, случайная компонента гетероскедастична. Описанная процедура иллюстрируется расчетами, приведенными на рис. 36. Рис.37 Формулу (2) можно преобразовать к виду, более удобному для расчета среднеквадратичного отклонения прогноза
Тогда Оценим дисперсию ошибки прогноза исходя из полученных ранее оценок:
Результаты оценки выполнены в Excel и представлены на рис. 37.
Исходные данные для задачи.
Данные о годовом располагаемом доходе и годовых расходах на личное потребление (в 1999 г., в условных единицах) 20 семей. Эти данные представлены в таблице 1.
Табл. 1.
Литература.
1. Бывшев В.А. Введение в эконометрию. Часть 2.-М.: ФА при Правительстве РФ, 2003. Лабораторная работа № 1 «Парная регрессия» Цель работы. Методом наименьших квадратов оценить коэффициенты линейной регрессии и провести проверку выполнения условий теоремы Гаусса-Маркова.
Основная спецификация математической модели имеет вид:
Условия теоремы накладывают ограничения на случайную компоненту Математическое ожидание Ковариация соседних значений Дисперсия случайной компоненты D( Если эти условия выполняются, то оценки неизвестных коэффициентов Сам метод наименьших квадратов (МНК) и вычислительные формулы для расчета оценок коэффициентов приводятся в учебном пособии [1]. Здесь же следует пояснить следующее. Исходными для вычисления коэффициентов регрессии являются табличные значения пар чисел {(X1,Y1), (X2,Y2),…,(Xn,Yn). Из формулы (1) видно, что в ее правой части стоит случайная величина
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.23.123 (0.335 с.) |

 (1)
(1)
 неизвестные коэффициенты регрессии, подлежащие оценке;
неизвестные коэффициенты регрессии, подлежащие оценке;  последовательность случайных величин, удовлетворяющих условиям теоремы Гаусса-Маркова, t = 1,2,…n.
последовательность случайных величин, удовлетворяющих условиям теоремы Гаусса-Маркова, t = 1,2,…n. и заключаются они в следующем:
и заключаются они в следующем: при
при  равна 0 -
равна 0 -  .
. = const.
= const. оказываются несмещенными (т.е. М(
оказываются несмещенными (т.е. М( ) =
) =  и М(
и М(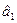 ) =
) =  ), эффективными (имеющих наименьшую дисперсию в классе всех линейных несмещенных оценок) и состоятельными (при большой выборке пар значений (Xt, Yt) D(
), эффективными (имеющих наименьшую дисперсию в классе всех линейных несмещенных оценок) и состоятельными (при большой выборке пар значений (Xt, Yt) D(






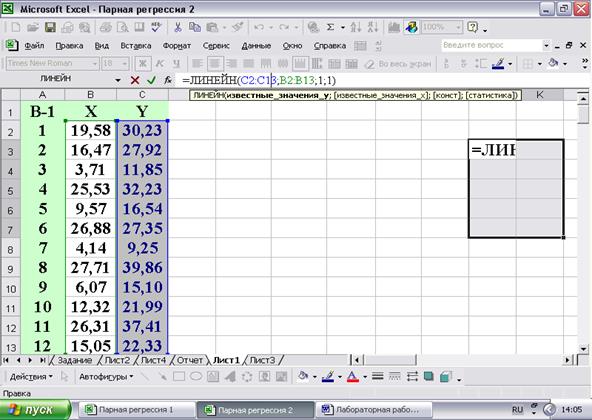


 и
и  . Среднеквадратичное отклонение составляет:
. Среднеквадратичное отклонение составляет:  = 2,074 и
= 2,074 и  = 0,113. В третьей строке справа указана оценка среднеквадратичного отклонения случайной составляющей εt и она равна
= 0,113. В третьей строке справа указана оценка среднеквадратичного отклонения случайной составляющей εt и она равна  = 3,418. Оценка дисперсии равна:
= 3,418. Оценка дисперсии равна: 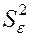 =3,4182 =11,68. Поскольку процесс моделировался с параметрами
=3,4182 =11,68. Поскольку процесс моделировался с параметрами  ,
,  = 1,
= 1, 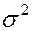 = 10, то можно утверждать, что получены неплохие оценки для такой выборки (n=12).
= 10, то можно утверждать, что получены неплохие оценки для такой выборки (n=12).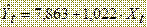 . Наихудший случай характеризуется значением R2 = 0. Он возникает в том случае, когда уравнение регрессии описывается одной константой
. Наихудший случай характеризуется значением R2 = 0. Он возникает в том случае, когда уравнение регрессии описывается одной константой  , которая в этом случае просто совпадает с
, которая в этом случае просто совпадает с  . По определению
. По определению  . Проверка значимости коэффициента R2 производится путем сравнения значения F-статистики, значение которой приводится в четвертой строке слева и равно 81,56, с критическим значением Fкр, определяемого функцией EXCEL FРАСПОБР из категории «Статистические».Для обращения к этой функции необходимо:
. Проверка значимости коэффициента R2 производится путем сравнения значения F-статистики, значение которой приводится в четвертой строке слева и равно 81,56, с критическим значением Fкр, определяемого функцией EXCEL FРАСПОБР из категории «Статистические».Для обращения к этой функции необходимо:
 > Fкр = 4,965 и это свидетельство того, что линейная регрессия хорошо описывает связь между эндогенной Yt и экзогенной Xt переменными.
> Fкр = 4,965 и это свидетельство того, что линейная регрессия хорошо описывает связь между эндогенной Yt и экзогенной Xt переменными. . Используем функцию EXCEL СРЗНАЧ в категории «Статистические».
. Используем функцию EXCEL СРЗНАЧ в категории «Статистические».



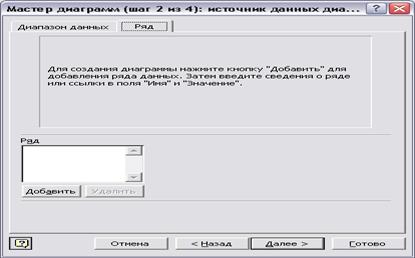


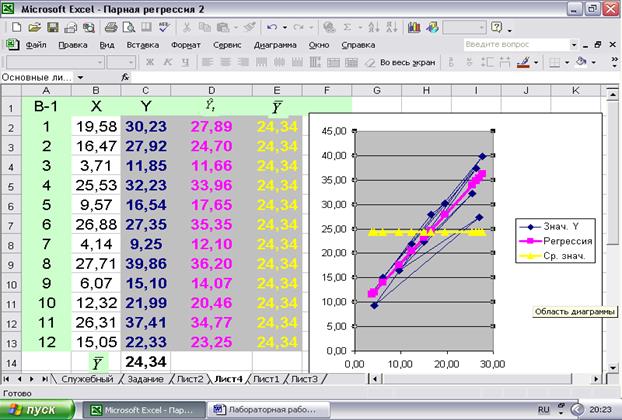


 Рис.25
Рис.25
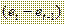 числителя статистики DW. Для вычисление сумм числителя и знаменателя DW используем функцию EXCEL СУММКВ (вычисление суммы квадратов значений, расположенных в ячейках вертикальной колонки). Результат представлен на рис. 32.
числителя статистики DW. Для вычисление сумм числителя и знаменателя DW используем функцию EXCEL СУММКВ (вычисление суммы квадратов значений, расположенных в ячейках вертикальной колонки). Результат представлен на рис. 32.

 . Из обеих частей формулы (2) извлечем квадратный корень:
. Из обеих частей формулы (2) извлечем квадратный корень:

 . Обозначим
. Обозначим  .
.
 , n = 12, Xp = 3,38., среднее значение Х, вычисленное с помощью функции СРЗНАЧ, равно
, n = 12, Xp = 3,38., среднее значение Х, вычисленное с помощью функции СРЗНАЧ, равно  .,
.,  .
.


