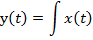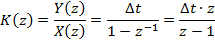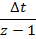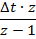Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переход от непрерывной передаточной функции к дискретной⇐ ПредыдущаяСтр 11 из 11
Воспользуемся дискретизацией импульсной характеристики

Если e-p∆t = z → z-преобразование
Разностное уравнение (z-1)Y(z)=zX(z) y[n+1]-y[n]=x[n+1] y[n+1]=y[n]+x[n+1]
Возможен переход к дискретной переходной функции с использованием формул численного интегрирования и заменой в передаточной функции операций аналогового интегрирования дискретным.
yi=yi-1+SABCD Приближенные методы а) Метод прямоугольников 1 yi=yi-1+∆t∙xi-1 z-преобразование Y(z)=z-1Y(z) +∆t∙z-1X(z) Y(z)(1-z-1)= ∆t∙z-1X(z)
б) Метод прямоугольников 2 yi=yi-1+∆t∙xi Y(z)=z-1Y(z) +∆t∙X(z)
в) Метод трапеций yi=yi-1+Sтрап ABCD = yi-1+∆t(xi-1+xi)/2 Z:
Операция по последовательному соединению интеграторов не соответствует операции последовательного соединения дискретных интеграторов.
Переход от непрерывной передаточной функции к дискретной совершается следующим образом: числитель и знаменатель непрерывной передаточной функции делится на p в высшей степени полинома знаменателя. В полученном выражении 1/p в соответствии степени знаменателя операцией дискретного интегрирования.
Например: моделирование интегрирующей цепи:
Моделирование узкополосных радиотехнических устройств
Для моделирования таких устройств характерно, что спектр сосредоточен на fн и в узком диапазоне.
При моделировании используются 3 метода: 1. Метод несущей 2. Метод комплексной огибающей 3. Метод информационного параметра Метод несущей При использовании этого метода модель фактически повторяет структуру моделирующего устройства, а частота дискретизации выбирается исходя из теоремы Котельникова. fд ≥ 2(fн+Fв) Модель радиоприемного устройства
При составлении модели по методу несущей системы автоподстройки не учитываются, но возможность изменения коэффициента передачи и частоты гетеродина предусматривается.
Недостаток моделирования – высокая тактовая частота. Для ее уменьшения используют масштабирования.
Используется два вида масштабирования: 1. Применяется по всем параметрам сигнала и устройства обработки одинаково.
Все процессы замедляются в Mt раз по сравнению с реальным временем. Такое масштабирование во много раз увеличивает время моделирования по сравнению с реальным. 2. Масштаб для несущей и огибающей различны
Такое масштабирование физически основано на том, что при изменении несущей частоты в каких-то пределах, огибающая не изменяется. Минимальное значение частоты дискретизации в этом случае определяется обобщенной теоремой Котельникова.
fдискр min ≥ 2∆f ≥ 4Fв Использование такого метода экономит время моделирования. Метод комплексной огибающей Метод несущей характеризуется избыточностью, т.к. сама несущая не несет полезной информации. В методе комплексной огибающей несущая вообще не учитывается, а моделирование ведется по комплексной огибающей. ВЧ сигнал: Um(t) – амплитудная модуляция ϕ(t) – угловая модуляция (ЧМ или ФМ) Устройство обработки является узкополосным, поэтому его импульсная характеристика является колебательной.
Для устройства обработки комплексная огибающая импульсной характеристики
При записи комплексной огибающей учтем, что центральная частота ВЧ колебаний может не совпадать с центральной частотой настройки устройства обработки
Модель построена по формуле свертки, которая справедлива для комплексной огибающей.
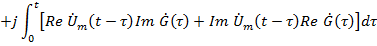
Основная трудность – подготовка математической модели.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.116.159 (0.015 с.) |

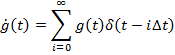

 – дискретное преобразование Лапласа (ДПЛ).
– дискретное преобразование Лапласа (ДПЛ).