
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка независимости генерируемых СВ
Двумерная плотность вероятности W(U1, U2)=W(U1)∙W(U2/U1) U1и U2 независимы, если их плотности распределения вероятности не зависят друг от друга: W(U1, U2)=W(U1)∙W(U2)
Экспериментально независимость случайных величин можно определить по двумерному распределению, когда на осях откладываются случайные величины. Наблюдаемые величины независимы, если изображения совместного распределения симметричны относительно осей параллельных осям U1и U2. Если оси симметрии наклонены, то случайные величины U1и U2 статически не зависимы. Для количественной оценки используют несколько разновидностей методов серии. Нужно определить независимость отсчетов СВ.
1. Переводится в последовательность нулей и единиц. 2. Находится вероятность превышения СВ U уровня U0.
Серия – последовательность одинаковых значений. Доказано, что количество серий для независимой последовательности подчиняется нормальному закону распределения, мат ожидание и дисперсия, которых зависят от числа элементов N и вероятности превышения порога.
Находится минимальное и максимальное значение количества серий Rmin и Rmax из условия, что вероятность выхода количества серий за эти рамки будет меньше 2ε.
Если найденное количество серий находится в пределах Rmin и Rmax, то последовательность значений случайной величины считается независимой.
Метод длины серий.
Строится оценка вероятности того, что серия имеет определенную длину. Теоретически распределение длины подчиняется закону Бернулли. ni – длина серии N – длина последовательности
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.66.151 (0.005 с.) |
 ; n0 – количество превышающих U0.
; n0 – количество превышающих U0.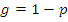
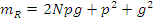


 ;
; 





