
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие параллельности двух прямых.
L|| N тогда и только тогда, когда S || R тогда и только тогда, когда Условие перпендикулярности двух прямых, L Любая прямая, перпендикулярная плоскости, называется нормаль ю к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектор ом плоскости. Замечание Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля. Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно. Теорема 1 Пусть вектор
является уравнением плоскости
Вектор
Выразив скалярное произведение в левой части этого равенства через координаты сомножителей по формуле
получим формулу Пусть r -- радиус-вектор текущей точки
Такое уравнение обычно называют векторным уравнением плоскости Раскроем скобки в уравнении
Такое уравнение называется общим уравнением плоскости. Еще раз отметим, что в этом уравнении хотя бы один из коэффициентов Верно и обратное утверждение: Теорема 2 Всякое уравнение (
Доказательство. Условие
По теореме 1 такое уравнение является уравнением плоскости с нормальным вектором n, проходящей через точку Рассмотрим теперь полное уравнение плоскости и покажем, что оно может быть приведено к следующему виду. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой: Поставим перед собой цель – вывести уравнение плоскости, проходящей через три различные точки М1(x1,y1,z1) M2 (x2, y2,z2) M3(x3,y3,z3), не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы М1 M2={ x2 - x1, y2- y1, z2- z1} и М1M3=={ x3 - x1, y3- y1, z3- z1} не коллинеарный, а поэтому точка М(x,y,z) лежит в одной плоскости с точками М1,M2, M3 , тогда и только тогда, когда векторы М1 M2 и М1M3 и М1 M={ x - x1, y- y1, z- z1} компланарны, т.е. тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю. Использую выражение смешанного произведения в координатах, мы получим необходимое и достаточное условие принадлежности М(x,y,z) к указанной плоскости в виде:
x2 - x1 y2- y1 z2- z1 =0 x3 - x1 y3- y1 z3- z1 уравнение первой степени и является уравнением искомой плоскости.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.109 (0.005 с.) |
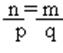
 N тогда и только тогда, когда S
N тогда и только тогда, когда S  =0
=0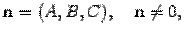 является нормальным вектором плоскости
является нормальным вектором плоскости 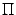 , проходящей через точку
, проходящей через точку 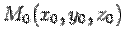 . Тогда уравнение
. Тогда уравнение
 Доказательство. Пусть
Доказательство. Пусть 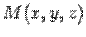 - некоторая точка плоскости
- некоторая точка плоскости 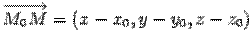 лежит на плоскости
лежит на плоскости 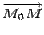 ортогонален вектору n. Если же взять точку Q, не лежащую на плоскости
ортогонален вектору n. Если же взять точку Q, не лежащую на плоскости 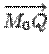 не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения, то условием того, что точка
не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения, то условием того, что точка 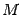 лежит в плоскости
лежит в плоскости 
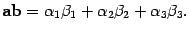

 - радиус-вектор точки
- радиус-вектор точки 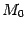 . Тогда уравнение
. Тогда уравнение 
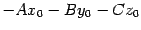 является числом, которое обозначим буквой
является числом, которое обозначим буквой 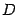 . Тогда уравнение
. Тогда уравнение 
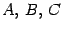 отличен от нуля, так как
отличен от нуля, так как  .
. , является уравнением плоскости, ортогональной вектору
, является уравнением плоскости, ортогональной вектору  .
.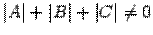 означает, что хотя бы одно из чисел
означает, что хотя бы одно из чисел  . Преобразуем уравнение
. Преобразуем уравнение  следующим образом:
следующим образом:
 .
. , называемому уравнением плоскости «в отрезках». Так как коэффициенты А В С D отличны от нуля то мы можем переписать уравнение в виду
, называемому уравнением плоскости «в отрезках». Так как коэффициенты А В С D отличны от нуля то мы можем переписать уравнение в виду  и затем положить a=-D/A, b=-D/B, c=-D/C. В уравнении плоскости в отрезках числа a, b и c имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает плоскость на осях Ох, Оу и Oz соответственно (отрезки отсчитываются от начала координат). Чтобы убедиться в этом, достаточно найти точки пересечения плоскости, определяемой уравнением плоскости в отрезках с уравнениями у=0 и z=0 оси Ох. Мы получим координаты точки пересечения х=а, y=0, z=0. Аналогично устанавливается, что координаты точки пересечения плоскости с осью Оу равны х=0, y=b, z=0 и с осью Oz равны х=0, y=b, z=с.
и затем положить a=-D/A, b=-D/B, c=-D/C. В уравнении плоскости в отрезках числа a, b и c имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает плоскость на осях Ох, Оу и Oz соответственно (отрезки отсчитываются от начала координат). Чтобы убедиться в этом, достаточно найти точки пересечения плоскости, определяемой уравнением плоскости в отрезках с уравнениями у=0 и z=0 оси Ох. Мы получим координаты точки пересечения х=а, y=0, z=0. Аналогично устанавливается, что координаты точки пересечения плоскости с осью Оу равны х=0, y=b, z=0 и с осью Oz равны х=0, y=b, z=с.



