Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление отрезка в заданном соотношении.Стр 1 из 5Следующая ⇒
Деление отрезка в заданном соотношении.
l=M1M/MM2 (*) называется отношением, в котором точка M делит направленный отрезок M1M2 . Таким образом, любая, отличная от M2 точка M делит отрезок M1M2 в некотором отношении l, где l определяется равенством (*). Уравнение прямой с угловым коэффициентом. Пусть заданы две прямые
Если Доказательство. Как известно из школьного курса математики, угловой коэффициент в уравнении прямой
что дает формулу Если же
Следовательно, Общее уравнение прямой. Докажем сначала, что если на плоскости П задана произвольная прямая линия L и фиксированная произвольная декартова прямоугольная систему Оху, то прямая L определяется в этой системе уравнением первой степени. Достаточно доказать, что прямая L определяется уравнением первой степени при каком-то одном специальном выборе декартовой прямоугольной системы на плоскости П, ибо тогда она будет определяться уравнением первой степени и при любом выборе декартовой прямоугольной системы на плоскости П. Направим ось Ох вдоль прямой L, а ось Оу перпендикулярно к ней. Тогда уравнением прямой будет уравнение первой степени у=0. в самом деле, этому уравнению будут удовлетворять координаты любой точки, лежащей на прямой L, и не будут удовлетворять координаты ни одной точки, не лежащей на прямой L. Докажем теперь, что если на плоскости П фиксирована произвольная декартова система Оху, то всякое уравнение первой степени с двумя переменными х и у определяет относительно этой системы прямую линию. В самом деле пусть фиксирована произвольная декартова прямоугольная системы Оху и задано уравнение первой степени Ах+Ву+с=0, в котором А В С- какие угодно постоянные, причем из постоянных А и В хотя бы одна отлична от 0. уравнение заведомо имеет хотя бы одно решение х0 и у0, т.е. существует хотя бы одна точка М(х0, у0) координаты которой удовлетворяют уравнению Ах0+Ву0+С=0. вычитая из уравнения первой степени уравнение где подставлена точка М(х0, у0), мы получим уравнение: А(х- х0)+В(у- у0)=0(1), эквивалентное уравнении первой степени. Достаточно доказать, что уравнение определяет относительно системы некоторую прямую. Мы докажем, что уравнение (1) определяет прямую L, проходящую через точку М(х0, у0) и перпендикулярную вектору n={A,B}. В самом деле, если точка М(х,у) лежит на указанной прямой L, то ее координаты удовлетворяют уравнению (1), ибо в этом случае векторы n={A,B} и М0М={x-x0,у-у0} ортогональныи их скалярное произведение А(х- х0)+В(у- у0) равно нулю. Если же точка М(х,у) не лежит на указанной прямой, то ее координаты не удовлетворяют уравнению (1), ибо в этом случае векторы n={A,B} и М0М={x-x0,у-у0} не ортогональны и поэтому их скалярное произведение не равно нулю. Утверждение доказано
Уравнение Ах+Ву+С=0 с произвольными коэффициентами А В иС такими, что А и В не равны нулю одновременно, называется общим уравнением прямой. Мы доказали, что прямая определяемая общим уравнением Ах+Ву+С=0 ортогональна к вектору n={A,B}. Этот последний вектор мы будем называть нормальным вектором прямой. Каноническое уравнение прямой. Любой ненулевой вектор, параллельный данной прямой, будем называть направляющим вектором этой прямой. Поставим перед собой задачу: найти уравнение прямой, проходящей через данную точку М1(х1,у1) и имеющей заданный направляющий вектор q={l,m}. Очевидно точка М(х,у) лежит на указанной прямой тогда и только тогда, когда векторы М1М={x-x1, y-y1} и q={m,l} коллинеарны, тогда и только тогда, когда координаты этих векторов пропорциональны, т.е.
Рассмотрим теперь полное уравнение плоскости и покажем, что оно может быть приведено к следующему виду.
Теорема о базисном миноре. Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор. Следствие1:Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему. Доказательство: Пусть ранг матрицы
Следствие2: Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему. Доказательство: Ранг матрицы при транспонировании не меняется. Строки матрицы становятся ее столбцами. Максимальное число новых столбцов транспонированной матрицы, (бывших строк исходной) образующих линейно независимую систему, равно рангу матрицы.
Следствие3: Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк). Доказательство: Пусть порядок матрицы
Теорема:Определитель матрицы равен нулю тогда и только тогда, когда один из ее столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
РАНГ СТУПЕНЧАТОЙ МАТРИЦЫ. Вспомним, что матрица вида называется ступенчатой матрицей. Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк. Поскольку доказано, что любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду, а элементарные преобразования не меняют ранга матрицы, то можно дать еще одно эквивалентное определение ранга матицы: ранг матрицы равен числу ненулевых строк в ступенчатой форме матрицы.
Это последнее определение позволяет вычислять ранг матрицы с помощью Гауссова исключения: для того, чтобы вычислить ранг матрицы, приводим ее Гауссовым исключением к ступенчатому виду и подсчитываем количество ненулевых строк. Ранг матрицы находится: либо методом окаймления миноров, либо методом элементарных преобразований. 1) При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k. Пример: Найти методом окаймления миноров ранг матрицы Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M2 = 2) Элементарными называются следующие преобразования матрицы: 1) перестановка двух любых строк (или столбцов), 2) умножение строки (или столбца) на отличное от нуля число, 3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число. Две матрицы называютсяэквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований. Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
Алгоритм нахождения ранга матрицы. Пусть требуется вычислить ранг матрицы Первую строку оставляем без изменений. Ко второй строке прибавляем первую, умноженную на число
Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке. Преобразованная матрица имеет вид Если все строки, начиная со второй, в полученной матрице нулевые, то ее ранг равен 1, так как есть минор первого порядка, отличный от нуля Если все строки, начиная с третьей, нулевые, то На каком-то этапе мы придем к матрице, у которой все строки, начиная с Системы линейных уравнений Определение: Системой
Систему (1) можно записать также в виде
или в виде
Но наиболее удобной формой записи системы (15.1) является матричная запись. Введем следующие матрицы: матрица системы
с помощью введенных обозначений систему (1) можно записать в виде
Однородная, неоднородная СЛАУ. МАТРИЧНЫЕ УРАВНЕНИЯ Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Найдем произведение т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением. Пусть определитель матрицы отличен от нуля | A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A:
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Формулы Крамера Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А: D = det (ai j) и n вспомогательных определителей D i (i= Формулы Крамера имеют вид: D × x i = D i (i = Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: x i = D i / D. Если главный определитель системы D и все вспомогательные определители D i = 0 (i= Теорема (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём Доказательство: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения: Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и Наконец несложно заметить, что Таким образом, получаем равенство: Аналогично выводятся равенства Теорема Кронекера - Капелли. Система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы Доказательство: Оно распадается на два этапа. 1. Пусть система имеет решение. Покажем, что Пусть набор чисел 2. Пусть
Положим
В силу равенства (1) В рассмотренной выше системе Замечание:Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса) Пусть дана система Выпишем расширенную матрицу системы
Назовем элементарными операциями следующие действия с матрицами: 1. перестановка строк; 2. умножение строки на число, отличное от нуля; 3. сложение строки с другой строкой, умноженной на число. Отметим, что при решении системы уравнений, в отличие от вычисления определителя и нахождения ранга, нельзя оперировать со столбцами. Если по матрице, полученной из Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице
(Первые нулевые столбцы, как правило, отсутствуют.) Если в матрице Этому уравнению не удовлетворяет ни один набор чисел Матрицу где
По отношению к матрице
где
и к матрице Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее. Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида
Далее выполняется так называемый обратный ход метода Гаусса. По матрице Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы Ax=b. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами Если система была однородной, то получим общее решение однородной системы. Коэффициенты при Способ 2: Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одной переменной, перенесенной в правую часть, нужно присвоить значение 1, а остальным - нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другой переменной в правой части значение 1, а остальным - нули, получим второе решение из фундаментальной системы и т.д. Определение: система называется совместно й, если она имеет хотя бы одно решение, и несовместной -- в противном случае, то есть в случае, когда решений у системы нет. Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных. Например, система из трех уравнений с двумя неизвестными
имеет решение
решений не имеет, то есть является несовместной. Определение: Расширенной матрицей системы линейных уравнений называется матрица
Следствие: Ранг расширенной матрицы Доказательство: Так как любая линейно независимая система столбцов матрицы A является линейно независимой системой столбцов матрицы Пусть Квадратные системы с невырожденной матрицей. Система называется квадратной, если число m ее уравнений равно числу n неизвестных, то есть когда ее матрица A -- квадратная матрица. Решение СЛАУ: Пусть дана СЛАУ
……. … …… Am1x1 + … + amnxn = 0 Данная система всегда совместна так как имеет тривиальное решение х1=…=хn=0 Для существования нетривиальных решений необходимо и достаточно выполнение словия r = r(A) < n, что равносильно условию det(A)=0, когда матрица А – квадратная. Th Совокупность решений СЛАУ образует линейное пространство размерности (n-r). Это означает, что произведение ее решения на число, а также сумма и линейная комбинация конечного числа ее решений является решениями этой системы. Линейное пространство решений любой СЛАУ является подпространством пространства Rn. Любая совокупность (n-r) линейно независимых решений СЛАУ (являющаяся базисом в пространстве решений) называется фундаментальной совокупностью решений(ФСР). Пусть х1,…,хr - базисные неизвестные, хr+1,…,хn – свободные неизвестные. Свободным переменным дадим поочередно следующие значения:
хr+2=0 хr+2=1 хr+2=0 …… …… …… хn=0 хn=0 хn=1
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.124.244 (0.119 с.) |
 Рассмотрим в пространстве две различные точки M1 и M2 и прямую, определяемую этими точками. Выберем на этой прямой некоторое направление. На полученной оси точки M1 и M2 определяют направленный отрезок M1M2. Пусть M – любая, отличная от M2 точка указанной оси. Число
Рассмотрим в пространстве две различные точки M1 и M2 и прямую, определяемую этими точками. Выберем на этой прямой некоторое направление. На полученной оси точки M1 и M2 определяют направленный отрезок M1M2. Пусть M – любая, отличная от M2 точка указанной оси. Число и
и  , (
, ( ). Тогда, если
). Тогда, если 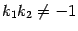 , то угол
, то угол  между этими прямыми можно найти из формулы
между этими прямыми можно найти из формулы
 , то прямые перпендикулярны.
, то прямые перпендикулярны. равен тангенсу угла
равен тангенсу угла  наклона прямой к оси
наклона прямой к оси  . Из рис. 11.10 видно, что
. Из рис. 11.10 видно, что  .
. Так как
Так как  ,
, 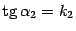 , то при
, то при 
 , откуда
, откуда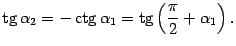
 и
и  .
.
 , называемому уравнением плоскости «в отрезках». Так как коэффициенты А В С отличны от нуля то мы можем переписать уравнение в виду
, называемому уравнением плоскости «в отрезках». Так как коэффициенты А В С отличны от нуля то мы можем переписать уравнение в виду  и затем положить А=-С/А b=-C/B. В уравнении плоскости в отрезках числа a, b имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает плоскость на осях Ох, Оу соответственно (отрезки отсчитываются от начала координат). Чтобы убедиться в этом, достаточно найти точки пересечения прямой, определяемой уравнением прямой в отрезках с осями координат. Например точка пересечения с осью Ох определяется из совместного рассмотрения уравнения прямой в отрезках с уравнением у=0 оси Ох. Мы получим координаты точки пересечения х=а у=0. Аналогично устанавливается, что координаты точки пересечения прямой с осью Оу имеют вид х=0 и у=b.
и затем положить А=-С/А b=-C/B. В уравнении плоскости в отрезках числа a, b имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает плоскость на осях Ох, Оу соответственно (отрезки отсчитываются от начала координат). Чтобы убедиться в этом, достаточно найти точки пересечения прямой, определяемой уравнением прямой в отрезках с осями координат. Например точка пересечения с осью Ох определяется из совместного рассмотрения уравнения прямой в отрезках с уравнением у=0 оси Ох. Мы получим координаты точки пересечения х=а у=0. Аналогично устанавливается, что координаты точки пересечения прямой с осью Оу имеют вид х=0 и у=b.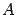 равен
равен 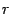 . Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. Этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно
. Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. Этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно 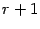 столбцов образуют линейно независимую систему. Составим из них матрицу
столбцов образуют линейно независимую систему. Составим из них матрицу  . Все миноры матрицы
. Все миноры матрицы  . Определитель является единственным минором квадратной матрицы, имеющим порядок
. Определитель является единственным минором квадратной матрицы, имеющим порядок 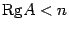 . Следовательно, система из
. Следовательно, система из 
 .
. , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
, отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно . Если матрица
. Если матрица  . В противном случае с помощью перестановки строк и столбцов матрицы добиваемся того, чтобы в левом верхнем углу матрицы стоял ненулевой элемент. Итак, считаем, что
. В противном случае с помощью перестановки строк и столбцов матрицы добиваемся того, чтобы в левом верхнем углу матрицы стоял ненулевой элемент. Итак, считаем, что  .
. . В результате вторая строка принимает вид
. В результате вторая строка принимает вид  Затем к третьей строке прибавляем первую строку, умноженную на число
Затем к третьей строке прибавляем первую строку, умноженную на число  . В результате третья строка принимает вид
. В результате третья строка принимает вид 

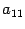 . В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что
. В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что  . Первую и вторую строки оставляем без изменений. К третьей строке прибавляем вторую, умноженную на число
. Первую и вторую строки оставляем без изменений. К третьей строке прибавляем вторую, умноженную на число  . В результате получим, что второй элемент третьей строки равен нулю. Затем к четвертой строке прибавляем вторую, умноженную на число
. В результате получим, что второй элемент третьей строки равен нулю. Затем к четвертой строке прибавляем вторую, умноженную на число  , и т.д. В результате получаем матрицу
, и т.д. В результате получаем матрицу 
 , так как минор
, так как минор  . В противном случае перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т.д.
. В противном случае перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т.д. -ой, равны нулю (или отсутствуют при
-ой, равны нулю (или отсутствуют при  ), а минор в первых
), а минор в первых  .
. линейных уравнений с
линейных уравнений с 


 и столбец свободных членов
и столбец свободных членов 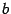 ,
,
 и неоднородной в противном случае.
и неоднородной в противном случае.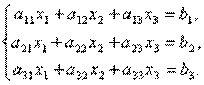 Рассмотрим матрицу системы
Рассмотрим матрицу системы 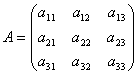 и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов 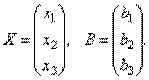
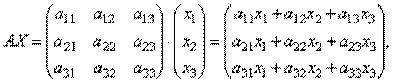
 или короче A ∙ X=B.
или короче A ∙ X=B.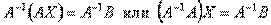 . Поскольку A-1A = E и E ∙ X = X, то получаем решение матричного уравнения в виде X = A-1B.
. Поскольку A-1A = E и E ∙ X = X, то получаем решение матричного уравнения в виде X = A-1B.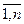 ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.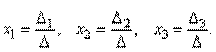

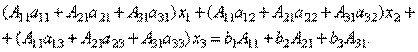
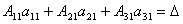 .
.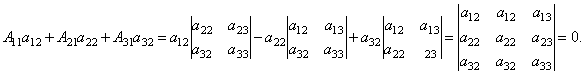
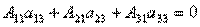 .
.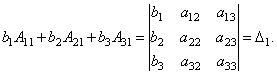
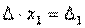 . Следовательно,
. Следовательно, 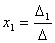 .
.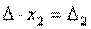 и
и  , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.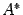 .
.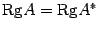 .
.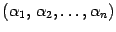 является решением системы. Обозначим через
является решением системы. Обозначим через 
 -ый столбец матрицы
-ый столбец матрицы  . Тогда
. Тогда  , то есть столбец свободных членов является линейной комбинацией столбцов матрицы
, то есть столбец свободных членов является линейной комбинацией столбцов матрицы 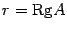 . Предположим, что
. Предположим, что 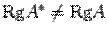 . Тогда по
. Тогда по  . Выберем в
. Выберем в 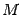 . Он имеет порядок
. Он имеет порядок  , где
, где  -- определитель, который получается из минора
-- определитель, который получается из минора  . Если столбец
. Если столбец  проходил через минор M, то в
проходил через минор M, то в  , будет два одинаковых столбца и, следовательно,
, будет два одинаковых столбца и, следовательно, 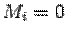 . Если столбец
. Если столбец  не проходил через минор
не проходил через минор  , то
, то 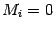 . Таким образом,
. Таким образом,  , что противоречит определению базисного минора. Значит, предположение, что
, что противоречит определению базисного минора. Значит, предположение, что 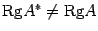 , неверно.
, неверно.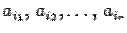 . Тогда по теореме о базисном миноре в матрице
. Тогда по теореме о базисном миноре в матрице 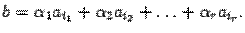
 ,
, 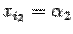 ,
,  ,
, 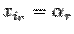 , остальные неизвестные возьмем равными нулю. Тогда при этих значениях
, остальные неизвестные возьмем равными нулю. Тогда при этих значениях 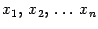 получим
получим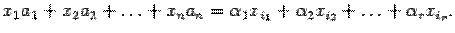
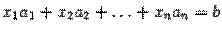 . Последнее равенство означает, что набор чисел
. Последнее равенство означает, что набор чисел  является решением системы. Существование решения доказано.
является решением системы. Существование решения доказано.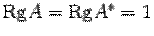 , и система является совместной. В системе
, и система является совместной. В системе  ,
,  , и система является несовместной.
, и система является несовместной.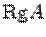 и
и 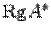 , ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.
, ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.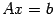 . Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя и к методу нахождения ранга матрицы. Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.
. Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя и к методу нахождения ранга матрицы. Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.
 . Тогда ко второй строке прибавим первую, умноженную на число
. Тогда ко второй строке прибавим первую, умноженную на число 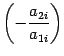 , к третьей строке прибавим первую, умноженную на число
, к третьей строке прибавим первую, умноженную на число 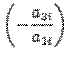 , и т.д. В результате получим матрицу
, и т.д. В результате получим матрицу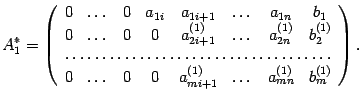
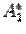 встретилась строка с номером k, в которой все элементы
встретилась строка с номером k, в которой все элементы 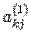 равны нулю, а
равны нулю, а 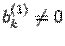 , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что
, то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что 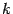 -ое уравнение будет иметь вид
-ое уравнение будет иметь вид 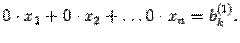
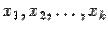 .
. можно записать в виде
можно записать в виде 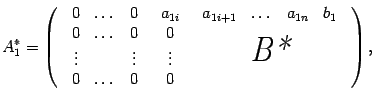

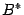 выполняем описанный шаг алгоритма. Получаем матрицу
выполняем описанный шаг алгоритма. Получаем матрицу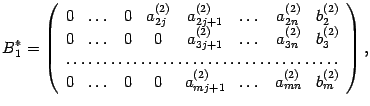
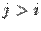 ,
, 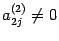 . Эту матрицу снова можно записать в виде
. Эту матрицу снова можно записать в виде
 снова применим описанный выше шаг алгоритма.
снова применим описанный выше шаг алгоритма.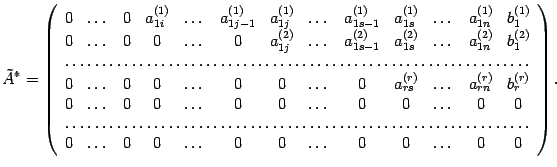
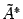 составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть
составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть  . Заметим, что
. Заметим, что 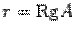 . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.
. Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.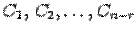 , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин
, включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин 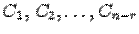 (в частности, просто произвольной величиной
(в частности, просто произвольной величиной 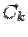 ). Эта запись и будет общим решением системы.
). Эта запись и будет общим решением системы.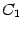 , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при
, взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при  -- второе решение и т.д.
-- второе решение и т.д.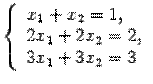
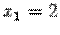 ,
, 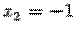 и даже имеет бесконечно много решений, а система из двух уравнений с тремя неизвестными
и даже имеет бесконечно много решений, а система из двух уравнений с тремя неизвестными

 , то в силу предложения 14.26 (Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему)
, то в силу предложения 14.26 (Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему)  .
. ,
, 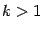 . Тогда в матрице
. Тогда в матрице  . Получили противоречие. Предположение, что k>1, неверно.
. Получили противоречие. Предположение, что k>1, неверно.
 A11x1 + … + a1nxn = 0
A11x1 + … + a1nxn = 0