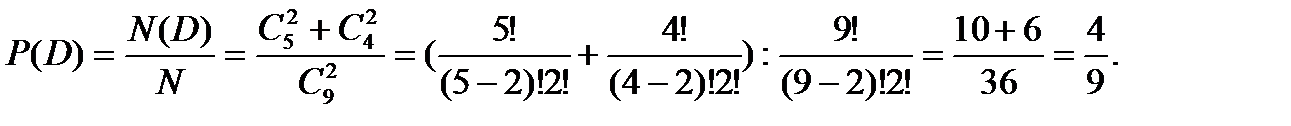Классический подход к понятию вероятности

 

В классическом походе к определению понятия вероятности рассматриваются частные случаи, в которых можно определить вероятность события без проведения большой серии испытаний. Этот подход предложен французским математиком П. Лапласом (1749−1817 гг.) и применим он только для моделей случайных событий с равновозможными исходами. Например, при рассмотрении опытов с бросанием игральной кости или монеты подразумевается, что они идеально симметричны, изготовлены из однородного материала, никогда не станут на ребро и не укатятся из поля зрения наблюдателя.

Определение. Событие В называется благоприятствующим событию A, если его наступление в результате испытания всегда приводит к наступлению события A.

Пример 3.18. Рассмотрим опыт с бросанием игральной кости. Пусть событие B – выпадение двойки на верхней грани игральной кости, а событие A – выпадение четного числа. Реализация в результате испытания события B всякий раз влечет за собой наступление события A, следовательно, событие B является благоприятствующим событию A.

Пример 3.19. Рассмотрим опыт, связанный с бросанием игральной кости, имеющий конечное число равновозможных, образующих полную группу исходов. В данном опыте возможны следующие исходы: U₁ – выпадение на верхней грани единицы, U₂ – двойки, U₃ – тройки, …, U₆ – шестерки. Действительно, события U₁, U₂, …, U₆ – попарно несовместны, т. к. в результате каждого испытания обязательно произойдет одно и только одно из этих событий.

При выполнении условия идеальной симметричности игральной кости (никакая из граней не утяжелена, грани кубика одинаковые и пр.) события U₁, U₂, …, U₆ в длинной серии испытаний реализуются с одинаковой частотой, т. е. являются равновозможными (равновероятными).

События, обладающие перечисленными свойствами, называются элементарными.

Определение. Элементарными событиями называются попарно несовместные, равновозможные события, образующие полную группу.

Совокупность элементарных событий называется пространством элементарных событий и обозначается Ω.

Пример 3.20. Рассмотрим опыт с бросанием монеты. Какие исходы в рамках данного опыта можно считать элементарными?

Элементарными являются следующие исходы (события): U₁ – выпадение орла, U₂ – выпадение решки. Действительно, если монета симметрична, то эти исходы являются равновозможными, попарно несовместными и образуют полную группу.

Пример 3.21. Рассмотрим опыт с бросанием двух монет. Какие исходы в рамках данного опыта можно считать элементарными?

С одной стороны, можно считать элементарными события: U₁ – выпадение на первой монете орла, U₂ – выпадение на первой монете решки, U₃ – выпадение на второй монете орла, U₄ – выпадение на второй монете решки. Действительно, перечисленные события удовлетворяют определению понятия элементарных событий.

С другой стороны, можно считать элементарными следующие события: H₁ – выпадение орла и на первой и на второй монетах, H₂ – выпадение решки и на первой и на второй монетах, H₃ – выпадение на первой монете решки, а на второй монете – орла, H₄ – выпадение на первой монете орла, а на второй монете – решки. События H_{1 ,} H_{2 ,} H₃ и H₄ также удовлетворяют определению понятия элементарных событий.

Необходимо отметить, что события U₁, U₂, U₃, U₄ и H_{1 ,} H_{2 ,} H₃, H₄ связаны между собой следующим образом:

H₁ =U₁× U₃, H₂ =U₂ × U₄, H₃ =U₂ × U₃, H₄ =U₁ × U_4.

Вывод. Оптимальный выбор элементарных событий часто значительно упрощает решение задачи.

Определение. Вероятностью события A называется отношение числа исходов N(A), благоприятствующих событию A, к полному числу элементарных исходов N:

(3.8)

Пример 3.22. Рассмотрим опыт с бросанием монеты. Найти вероятность выпадения орла. Обозначим через A событие, связанное с выпадением орла. В рамках условия задачи всего два элементарных исхода: U₁ – выпадение орла, U₂ – выпадение решки. Из них благоприятным событию A является только одно. С помощью формулы (3.8) найдем вероятность события A:

Пример 3.23. Рассмотрим элементарные исходы, связанные с бросанием двух монет: H₁ – выпадение орла и на первой и на второй монетах, H₂ – выпадение решки и на первой и на второй монетах, H₃ – выпадение на первой монете решки, а на второй монете – орла, H₄ – выпадение на первой монете орла, а на второй монете – решки. Можно ли считать исходы H₃ и H_4, связанные с выпадением на одной монете орла, а на другой – решки, в одном испытании? Поставленный вопрос можно сформулировать иначе: сколько существует в рамках этой задачи элементарных исходов 3 или 4?

При классическом подходе к понятию вероятности, когда проводят лишь мысленный эксперимент, ответить на поставленный вопрос невозможно. Однако результаты реальных экспериментов, связанных с достаточно большими сериями испытаний, позволяют утверждать, что при проведении опыта с бросанием более чем одной монеты, более чем одного кубика и пр., монеты, кубикии т. д. различимы. Таким образом, исходы H₃ и H₄ являются различными исходами, следовательно, в рассматриваемой задаче 4 элементарных исхода. Следовательно, вероятности событий H₁ – выпадения орла и на первой и на второй монетах и H₂ – выпадение решки и на первой и на второй монетах равны, т. к. только один исход является благоприятствующим этим событиям, а всего элементарных исходов – четыре, используя формулу (3.8), получим:

Вероятность события H, связанного с выпадением на одной монете орла, а на другой – решки, т. е. события H = H₃ + H₄, равна 1/2, т. к. два исхода являются благоприятными этому событию, а всего элементарных исхода – четыре, используя формулу (3.8), получим:

3.26. Рассмотрим опыт с бросанием двух монет. Найти вероятность выпадения:

а) хотя бы одного орла;

б) хотя бы одной решки;

в) не менее одной решки.

3.27. При проведении испытания с бросанием игральной кости найти вероятность выпадения на верхней грани кости:

а) шести очков;

б) пяти очков;

в) менее одного очка;

г) не более двух очков;

д) хотя бы трех очков;

ж) не менее пяти очков.

з) не менее двух и не более пяти очков.

Решение вероятностных задач

С помощью комбинаторики

 

Комбинаторику используют только для решения вероятностных задач с равновозможными исходами, т. е. в рамках классического подхода к понятию вероятности.

Пример 3.24. В урне 5 белых и 4 черных шара. Найти вероятность события: A – вытащить наугад белый шар, B – вытащить наугад два белых шара, C – вытащить наугад один белый и один черный шар, D – два шара одного цвета.

Число всех элементарных исходов при вытаскивании из урны наугад одного шара равно 9 или − числу сочетаний из девяти элементов по одному, т. к. всего шаров в урне 9 и выбрать один из них можно девятью способами. Благоприятствующих событию A исходов – пять или , поскольку белый шар можно вытащить из 5 белых шаров, следовательно, имеем:

Число всех элементарных исходов при вытаскивании из урны наугад двух шаров из 9 равно − числу сочетаний из девяти элементов по два. Учитывая, что число благоприятствующих событию B исходов соответственно равно , получим:

При нахождении вероятности события C – вытащить наугад один белый и один черный шар, число всех элементарных исходов также равно . Число благоприятствующих событию C исходов найдем используя правило произведения комбинаторики. Множество белых шаров содержит пять элементов, а множество черных – четыре, тогда число пар, образованных из элементов этих множеств, равно произведению количества элементов в этих множествах, т. е. Тогда вероятность события C равна:

Теперь найдем вероятность события D – вытащить два шара одного цвета, которое состоит в выборе наугад двух белых или двух черных шаров. Число всех элементарных исходов по прежнему равно . Используя правило суммы комбинаторики, получим, что число благоприятствующих событию D исходов равно , т. к. число способов выбора двух элементов из множества, содержащего пять элементов или из множества, содержащего четыре элемента (множества не пересекаются), равно сумме числа способов выбора двух элементов из каждого множества. Число всех элементарных исходов по прежнему равно . Учитывая вышеизложенное, получим:

Пример 3.25. В опыте с бросанием двух игральных костей найти вероятности выпадений в сумме на верхних гранях U₂ – двух очков, U₃ – трех очков, U₄ – четырех очков, …, U₁₂ – двенадцати очков.

Используяправило произведения комбинаторики, найдем число всех элементарных исходов, учитывая, что множество исходов при бросании первой кости содержит шесть элементов и множество исходов при бросании второй кости также содержит шесть элементов. Тогда число пар, образованных из элементов этих множеств, равно произведению количества элементов этих множеств, т. е.

Учитывая, что событиям U₂ и U₁₂ благоприятны по одному исходу – выпадение единиц на двух костях и соответственно выпадение шестерок на двух костях, найдем вероятности этих событий:

Событию U₃ благоприятны два исхода: выпадение на первой кости единицы и на второй – двойки или выпадение на первой кости двойки и на второй – единицы, так как известно (3.8.), что при бросании двух и более костей (монет) они всегда считаются различимыми. Учитывая, что событию U₁₁ также благоприятны два исхода: выпадение на первой кости пятерки и на второй – шестерки или наоборот, получим:

Событию U₄ благоприятны три исхода: выпадение на первой кости единицы и на второй – тройки или выпадение на первой кости тройки и на второй – единицы или выпадение двух очков и на первой и на второй костях. Заметим, что событию U₁₀ также благоприятны три исхода: выпадение на первой кости шестерки и на второй – четверки или выпадение на первой кости четверки и на второй – шестерки или выпадение пяти очков и на первой и на второй костях, следовательно, имеем:

Рассуждая аналогичным образом, получим:

Заметим, что событие, связанное с выпадением в сумме на верхних гранях двух игральных костей числа очков не менее двух и не более двенадцати является достоверным и его вероятность равна единице. Поскольку в каждом испытании одно из событий, состоящих в выпадении от двух до двенадцати очков включительно, обязательно произойдет, а суммарная вероятность рассматриваемых событий равна единице.

Для большей наглядности, представим полученные результаты в виде таблицы 3.4:

Таблица 3.4

Распределение очков в опыте

с бросанием двух игральных костей

Число очков

 

3.28. В опыте с бросанием двух игральных костей найти вероятность выпадения в сумме на верхних гранях:

а) менее трех очков;

б) более девяти очков;

в) более четырех и менее десяти;

г) хотя бы девяти очков.

3.29. Числа от 1 до 100 записывают на отдельных одинаковых карточках, помещают их в вазу и тщательно перемешивают. После этого наугад извлекают одну карточку. Найти вероятность события:

а) на карточке написано число, делящееся на 3;

б) на карточке написано число, делящееся на 3 и на 5;

г) на карточке написано число больше 90;

д) на карточке написано число больше 10 и меньше 20;

е) на карточке написано число, делящееся на 5, но не делящееся на 7.

Существует ли событие, связанное с этим опытом, вероятность которого равна 0,11? Если да, то какое это событие?

3.30. В урне 6 белых, 7 черных и 3 красных шаров. Найти вероятность события: A – вытащить наугад красный шар, B –вытащить наугад три шара разного цвета, C – вытащить наугад три шара так, чтобы хотя бы один шар был белым, D – вытащить наугад три шара так, чтобы два шара были белыми и один черный.

3.31. В урне 5 белых, 3 черных и 8 красных шара. Найти вероятность события: A – вытащить наугад черный шар, B – вытащить наугад три шара разного цвета, C – вытащить наугад три шара так, чтобы хотя бы один шар был красным, D – вытащить наугад три шара так, чтобы два шара были белыми и один красный.

3.32. Известно, что среди 15 книг имеется 5 бракованных, внешне не отличимых от доброкачественных. Наугад выбирается 5 книг. Найти вероятность события:

а) все 5 книг доброкачественные;

б) все 5 книг бракованные;

в) среди выбранных 5 книг ровно 2 бракованные;

г) среди выбранных 5 книг не более двух бракованных;

д) среди выбранных 5 книг не менее двух бракованных;

ж) среди выбранных 5 книг хотя бы три доброкачественные;

з) среди выбранных 3 книг по крайней мере две доброкачественные;

и) все выбранные 4 книги доброкачественные или бракованные.