
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ФЧХ рекурсивного фильтра первого порядка
Фазово-частотная характеристика рекурсивного ЦФ первого порядка может быть получена из выражения (15)
- 117 -
Рис.8. АЧХ рекурсивного фильтра 1-го порядка при a0=1, b1=-0.9. В полосе 0 – 1/2Т реализован фильтр верхних частотФВЧ.
Рис.9. АЧХ рекурсивного фильтра 1-го порядка при a0=1, b1=0.9. В полосе 0 – 1/2Т реализован фильтр нижних частотФНЧ.
- 118 - 3. Дискретное преобразование Фурье
При использовании численных методов спектрального анализа непрерывных сигналов, заданных на конечном временном интервале T, эти сигналы подвергают дискретизации во времени. Чаще всего используется постоянный интервал дискретизации Dt. Отсчетные значения после преобразования в цифровую форму записывают в виде временного ряда в некоторый массив x[i]. Далее определяют коэффициенты разложения. Если ряд Фурье задан в комплексной форме, то для коэффициентов разложения cn непрерывного процесса x(t) справедливо соотношение (1)
Для дискретного во времени процесса выражение (1) должно быть преобразовано следующим образом. 1. Вместо интеграла должна быть использована интегральная сумма. 2. Интервал времени усреднения 3. k -е отсчетное значение будет соответствовать текущему времени
Формула (19) определяет дискретное преобразование Фурье (ДПФ) в области комплексных чисел. В области действительных чисел формулы ДПФ могут быть определены следующим образом
Индекс k определяет порядковый номер отсчетного значения x[i]. Коэффициенты an bn позволяют получить оценку составляющих спектральной плотности мощности СПМ.
- 119 - Согласно (3-5) при нахождении каждого значения Sn приходится 2N раз вычислять значения тригонометрических функций. В практических приложениях число N отсчетных значений редко бывает меньше 1024. При этом время вычисления амплитуды каждой гармоники может достигать долей секунды, т.к. вычисление тригонометрических функций является относительно медленной операцией. Обычно ДПФ осуществляется для всех гармоник, т.е. при n=0, 1, 2,...N/2. В этом случае общее время вычисления СПМ по одному массиву может составлять десятки секунд, что является неприемлемым для расчетов в реальном масштабе времени, а также при получении состоятельных оценок СПМ случайных сигналов, т.к. для получения необходимой статистической точности каждую из гармоник приходится усреднять по нескольким десяткам реализаций.
В современных компьютерах процессор оснащен математическим сопроцессором, который существенно сокращает время вычисления гармонических функций. Если в вычислительном устройстве такого сопроцессора нет, то для сокращения времени вычисления тригонометрических функций целесообразно использовать следующие рекуррентные формулы
где Проведем оценку диапазона анализируемых частот с помощью ДПФ. Частота fn самой низкочастотной гармоники определяется интервалом времени усреднения
где fd - частота дискретизации случайного процесса. Частота fв самой высокочастотной анализируемой гармоники согласно теореме Котельникова равна половине частоты дискретизации
Сопоставление (9) и (10) показывает, что
- 120 - Таким образом, при проведении ДПФ для выборки случайного процесса объемом N целесообразно вычислять и отображать только N/2 гармоник, хотя чисто формально ДПФ позволяет вычислять N гармоник. Далее приведен текст программы дискретного преобразования Фурье применительно к m -связным случайным последовательностям. Программа осуществляет следующие операции: 1) Задание начальных параметров вычислений (N, m); В цикле repeat осуществляются следующие операции: 2) расчет и занесение в массив x[i] N отсчетных значений Марковского случайного процесса с детерминированной заменой составляющих (процедура Markov); 3) построение нормированного графика Марковского случайного процесса; 4) Выполнение дискретного преобразования Фурье с занесением в массивы a[j], b[j] компонент ДПФ; 5) Вычисление спектральной плотности мощности в массиве s[i]; 6) Построение нормированного графика СПМ в двойном логарифмическом масштабе. Применение такого масштаба позволяет существенно повысить точность отображения СПМ в области малых значений аргумента (частоты) и самой функции.
Завершение цикла repeat происходит по нажатию любой клавиши. Основными и принципиальными недостатками программы ДПФ является следующее: 1) Нерациональное использование объема памяти. 2) Низкое быстродействие вычисления ДПФ. Текст программы дискретного преобразования Фурье
uses graph, crt; type aa= array[0..4096] of real; var i,j,n,n1,m,Gd,Gm,x0,xm,x1,y0,ym,y1,xx,yy: integer; c,c1,max,min,a1,a2: real; w,jj: longint; tt: string; s,x,a,b,z:^aa; {================ Markov ===================} procedure Markov; var ss: real; ii,i2,k: integer; begin randomize; ss:=0; k:=1; for ii:=1 to M do z^[ii]:=random-0.5; - 121 - for ii:=1 to M do ss:=ss+z^[ii]; for i2:=0 to N do begin x^[i2]:=ss/M; ss:=ss-z^[k]; z^[k]:=random-0.5; ss:=ss+z^[k]; if k<M then inc(k) else k:=1; end; end; {---------------------------------------} begin new(s); new(x); new(a); new(b); new(z); w:=1; M:=30; N:=1024; x0:=50; xm:=600; c1:=(xm-x0)/N; gotoxy(10,1);write('N = ',N:5);gotoxy(50,1); if readkey<>#13 then readln(n); gotoxy(10,2);write('M = ',M:5);gotoxy(50,2); if readkey<>#13 then readln(m); Gd:=EGA; GM:=EGAHI; InitGraph(Gd,Gm,''); setbkcolor(15); For i:=0 to N div 2 do s^[i]:=1e-30; repeat if odd(w) then begin SetVisualPage(0); SetActivePage(1) end else begin SetVisualPage(1); SetActivePage(0);end; clearviewport; setcolor(1); {=========== Noise =================} y0:=5; ym:=80; y1:=y0+(ym-y0) div 2; outtextxy(GetMaxX-10,(y0+ym) div 2,'1'); line(x0,y1,xm+20,y1); line(x0,y0,x0,ym); Markov; {********************************************************} Max:=1e-18; for i:=0 to N do if Max<abs(x^[i]) then Max:=abs(x^[i]); c:=(ym-y1)/max; moveto(x0,y1-round(c*x^[1])); For i:=1 to N do lineto(x0+round(i*c1),y1-round(c*x^[i])); {======================= PSD ==========================} y0:=110; ym:=310; y1:=y0+(ym-y0) div 2; outtextxy(GetMaxX-10,y1,'2'); {------------- DFT -------------------------------} for i:=1 to n div 2 do begin a^[i]:=0; b^[i]:=0; a1:=2*pi*i/n; for j:=1 to n-1 do begin a2:=a1*j; a^[i]:=a^[i]+x^[j]*cos(a2); b^[i]:=b^[i]+x^[j]*sin(a2); end; end; {----------------------------------------------------}
- 122 - n1:=n div 2;Max:=1e-30;Min:=1e30; for i:=1 to N1 do s^[i]:=s^[i]+a^[i]*a^[i]+b^[i]*b^[i]; for i:=2 to N1 do begin if Max<s^[i] then Max:=s^[i]; if Min>s^[i] then Min:=s^[i]; end; str((max/w):10:3,tt);outtextxy(10,getmaxy-10,'So = '+tt); {--------------- Graphic -----------------------------} jj:=1; setlinestyle(1,1,1); For i:=0 to 3 do begin xx:=x0+round((xm-x0)*i*ln(10)/ln(N1-1)); if xx<=xm then begin line(xx,y0,xx,ym); str(jj:4,tt); outtextxy(xx+i*5-27,ym+10,tt); end; jj:=jj*10; end; c:=(ym-y0)/(ln(Max/Min)); {--------- Vertical -------------------} jj:=1000; For i:=0 to 8 do begin yy:=y0+round(c*i*ln(10)); if yy<=ym then begin line(x0,yy,xm,yy); outtextxy(x0-37,yy,'10'); str(-i,tt);outtextxy(x0-20,yy-4,tt);end; jj:=jj div 10; end; setlinestyle(0,0,1); rectangle(x0-3,y0-3,xm+3,ym+3); {----------- Plot ----------------------} moveto(x0,ym-round(c*ln(s^[2]/min))); for i:=3 to N1-1 do begin yy:=ym-round(c*ln(s^[i]/Min)); xx:=x0+round((Xm-x0)*ln(i-1)/ln(N1-1)); lineto(xx,yy); end; {----------------------------------------} str(w:10,tt);outtextxy(550,1,tt); if w<100000 then inc(w) else w:=1; until keypressed; closegraph; end.
4. Алгоритм быстрого преобразования Фурье
Запишем N- точечное дискретное преобразование Фурье для входной последовательности Xm.
- 123 - Разделим входную последовательность Xm отсчетных значений на четные Am и нечетные Bm отсчеты
Обозначим через
Из (2-3) видно, что одно N -точечное ДПФ можно заменить двумя N/2 -точечными ДПФ. Такая замена позволяет существенно уменьшить количество операций, затрачиваемых на вычисление всех компонент ДПФ. Рис.10 иллюстрирует процедуру вычисления ДПФ, получившую название «прореживание по времени». В этой процедуре выполняется замена одного 8-точечного ДПФ двумя 4-точечными ДПФ. Процедура замены результатов действия двух N/2 -точечных на N -точечное ДПФ согласно выражению (3) получила в литературе название «бабочка». На рис.10 эта операция обозначена в виде точек с заливкой в пересечении соответствующих линий.
Рис. 10. Алгоритм вычисления ДПФ с прореживанием по времени. Реализация 8-точечного ДПФ с помощью двух 4-точечных ДПФ.
Оценим выигрыш по количеству операций, затрачиваемых на вычисление ДПФ различными способами. Для N -точечного ДПФ необходимо выполнить N2 операций умножения отсчетных значений на значения
- 124 - соответствующей гармонической функции. Для N/2 -точечного ДПФ необходимо выполнить 2*(N/2)2 операций умножения отсчетных значений на значения соответствующих гармонических функций и N/2 операций умножения преобразованных значений на экспоненту. Общее сокращение количества операций составит т.е. примерно в 2 раза. Если N является целой степенью числа 2, то такой процесс замены количества точек в ДПФ можно продолжить и далее до 2-точечного ДПФ включительно. В 2-точечном ДПФ не требуется умножения отсчетных значений на гармоническую функцию, поскольку последняя принимает лишь два возможных значения +1 и –1. За счет этого в 2-точечном ДПФ необходимо нахождение лишь суммы и разности двух отсчетных значений. Соответствующий алгоритм, использующий такую последовательную замену на ДПФ с меньшим количеством точек до 2-точечного ДПФ, получил название быстрого преобразования Фурье (БПФ). Общий выигрыш по количеству операций при использовании БПФ составляет
Например, если N=2048, то объем вычислений при использовании БПФ, по сравнению с ДПФ сократиться в
Рассмотрим текст процедуры БПФ, которая может быть использована при работе в среде Турбо-Паскаля или Delphi. 1) Процедура БПФ состоит из двух частей: собственно преобразования Фурье и циклов перестановок преобразованных значений x[i], y[i] в порядке возрастания частоты. 2) Входной процесс и результат БПФ в комплексной форме записываются в одни и те же массивы x[i], y[i]. БПФ выполняется в трех вложенных циклах. Двухточечное комплексное ДПФ осуществляется во внутреннем цикле. 3) Объем выборки N, обозначенный через Num, обязательно должен быть равен 2MM1, где MM1 - целое число. 4) Расчет значений синуса и косинуса, необходимых для выполнения вычислений по формуле (3), осуществляется по рекуррентным формулам, аналогичным рассмотренным ранее. При этом s=sin(2p/N), c=cos(2p/N). Текущее значение косинуса заносится в U1, синуса - в U2. 5) Описанная процедура БПФ позволяет вычислять как прямое (inv=1), так и обратное (inv=-1) преобразование Фурье.
- 125 - Текст процедуры быстрого преобразования Фурье
procedure FFT(Nn,inv:integer); var t1,t2,U1,U2,U3,C: real; MM1,L0,L,L1,J,i1,N1,N2,k: integer; Begin MM1:=round(ln(Nn)/ln(2)); L0:=Num; {------------------------ Блок БПФ -------------------------} for L:=1 to MM1 do begin L1:=L0 div 2; U1:=1; U2:=0; C:=cos(pi/L1);
S:=inv*sin(pi/L1); for j:=1 to L1 do begin {---------------- Начало внутреннего цикла -----------------} i:=j; while i<=Num do begin i1:=i+L1; T1:=x[i]-x[i1]; T2:=y[i]-y[i1]; x[i]:=x[i]+x[i1]; y[i]:=y[i]+y[i1]; x[i1]:=T1*U1-T2*U2; y[i1]:=T2*U1+T1*U2; i:=i+L0; end; u3:=U1*c-U2*s; U2:=U2*c+U1*s; U1:=U3; end; L0:=L0 div 2; end; {----------------- Перестановки -------------------------} N2:=Num div 2; N1:=Num-1; j:=1; for i:=1 to N1 do begin if i<j then begin T1:=x[j]; T2:=y[j]; x[j]:=x[i]; y[j]:=y[i]; x[i]:=T1; y[i]:=T2; end; k:=N2; while k<j do begin j:=j-k; k:=k div 2; end; j:=j+k; end; end;
- 126 – Литература
1. Теория электрической связи / А.Г. Зюко, Д.Д. Кловский, В.И. Коржик, М.В. Назаров; Под ред. Д.Д. Кловского. – М.: Радио и связь, 1998, - 432 с. 2. Гоц С.С. Основы построения и программирования автоматизированных систем цифровой обработки сигналов. –Уфа, 2006, 212 с. 3. Гоц С.С. Основы описания и компьютерных расчетов характеристик случайных процессов в статистической радиофизике. Уфа, 2005, 166 с 4. Гоц С.С. Основы радиоэлектроники. Курс лекций. – Уфа, 2007. 137 с 5. Теория информации и кодирование / Самсонов Б.Б., Плохов Е.М., Филоненков А.И., Кречет Т.В. – Ростов на Дону, 2002, 288 с. 6. Гольденберг Л.С. и др. Цифровая обработка сигналов. – М.: Радио и связь, 1990. 256 с 7. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Радио и связь, 1986. 512 с 8. Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2003, 462 с. 9. Кларк Дж. Мл, Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. Пер. с англ.- М:. Радио и связь, 1987. – 392 с. 10. Сергиенко А.Б. Цифровая обработка сигналов.- СПб.:Питер, 2003, 608 с. 11. Каганов В.И. Радиотехнические цепи и сигналы.- М.: Академия, 2003, 224 с 12. Бытовая приемно-усилительная аппаратура / Под ред. К.Е.Румянцева. – М.: Академия, 2003, 304 с. 13. Цифровое ТВ: От студии к телезрителю. Компания “Сайрус”. WWW.Syrus.ru 14. Телекоммуникационные системы и сети. Т.2 / Катунин Г.П., Мамчев Г.В., Папантонопуло В.Н., Шувалов В.П. – Новосибирск: ЦЭРИС, 2000,, 624 с. 15. Прокис Дж. Цифровая связь. Пер. с англ. Под ред. Кловского Д.Д. – М.: Радио и связь, 2000, 800 с. 16. Цифровое преобразование изображений / Р.Е.Быков, К.В.Иванов, А.А.Манцветов. – М.: Горячая линия – Телеком, 2003. – 228 с. 17. Шмалько А.В. Цифровые сети связи: основы планирования и построения. – М.: Эко-Трендз, 2001, 282 с. 18. Цифровые и аналоговые системы передачи / В.И.Иванов, В.Н.Гордиенко, Г.Н.Попов и др. – 2-е изд. – М.: Горячая линия- Телеком, 2003. – 232 с 19. Вокодерная телефония. Методы и проблемы. Под ред. А.А.Пирогова. М.: Радио и связь, 1974. 535 с. 20. Куприянов А.И., Сахаров А.В., Шевцов В.А. Основы защиты информации. – М.: Академия, Радиоэлектроника, 2006. 256 с
- 127 –
|
||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.126.74 (0.096 с.) |
 . (17)
. (17)

 . (1)
. (1) .
. . С учетом этих замечаний
. С учетом этих замечаний . (2)
. (2) . (3)
. (3) . (4)
. (4)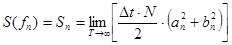 , (5)
, (5) (6)
(6)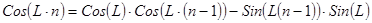 , (7)
, (7) . В компьютерах, не оснащенных математическими сопроцессорами, применение (6) (7) позволяет сократить время вычисления ДПФ в 4-6 раз.
. В компьютерах, не оснащенных математическими сопроцессорами, применение (6) (7) позволяет сократить время вычисления ДПФ в 4-6 раз. , (8)
, (8) . (9)
. (9) . (10)
. (10) . (1)
. (1) . (2)
. (2) и
и  k -е компоненты преобразованных по ДПФ последовательностей Ai и Bi.. Тогда (2) можно записать более компактно
k -е компоненты преобразованных по ДПФ последовательностей Ai и Bi.. Тогда (2) можно записать более компактно . (3)
. (3)
 раза,
раза, раз.
раз. раз.
раз.


