
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Филиал Санкт-Петербургского государственного морскогоСтр 1 из 3Следующая ⇒
Филиал Санкт-Петербургского государственного морского технического университета СЕВМАШВТУЗ И.С. Лобанова Е.В. Савченко И.В. Шерягин
Линейная алгебра. Аналитическая геометрия Учебное пособие
Северодвинск УДК 512
Лобанова И.С., Савченко Е.В., Шерягин И.В. Линейная алгебра. Аналитическая геометрия. Учебное пособие. – Северодвинск: РИО Севмашвтуза, 2005. – 88 с.
Ответственный редактор к.т.н., доцент И.С. Лобанова.
Рецензенты: зав. кафедрой алгебры и геометрии ПГУ им. М.В.Ломоносова к.ф.-м. н., доцент П.Д. Андреев; к.т. н., доцент Севмашвтуза Л.В.Кремлева. Учебное пособие предназначено для студентов, обучающихся по заочной форме обучения по специальности 06.08.00 «Экономика», которые изучают курс высшей математики. Пособие рассчитано на первый семестр обучения, включает в себя теоретический и практический материал по двум разделам: линейная алгебра и аналитическая геометрия. В учебное пособие входит контрольная работа за I семестр обучения, задачи с решениями, необходимыми для выполнения контрольной работы. Учебное пособие ставит своей целью обеспечение усвоения студентами данного курса.
ВВЕДЕНИЕ
Учебное пособие курса «Линейная алгебра. Аналитическая геометрия» предназначено для студентов, обучающихся по заочной форме обучения по специальности 06.08.00 «Экономика», изучающих курс высшей математики. Настоящее пособие разработано в соответствии с требованиями Государственного стандарта Министерства образования РФ 2000 года по подготовке специалистов по специальности экономист-менеджер. Особенность учебного пособия состоит в том, что в нем в аккумулятивной форме отражены все основные положения курса. Каждый раздел пособия содержит все наиболее существенные определения и теоремы и снабжен большим количеством примеров. Необходимость в таком пособии обусловлена тем, что в настоящее время имеющиеся учебники, во-первых, объемны, во вторых, большинство из них содержат либо только теоретические положения, либо задания и не содержат примеров решения. Кроме того, студентам, особенно заочного отделения, бывает крайне затруднительно извлекать из множества источников необходимую информацию для усвоения вопросов курса высшей математики. Контрольная работа №1 включает в себя задания 1-4; контрольная работа №2 включает в себя задания 5-14.
Матрицы и определители Понятие матрицы
Матрицей называется всякая таблица элементов, состоящая из m строк и n столбцов. Говорят, что число m´n называется размерностью матрицы.
Обозначение:
Размерность: dimA=m´n. аij -элемент матрицы, стоящий в i -той строке и j -том столбце.
Пример. размерность матрицы: dim A = 2´3, элементы матрицы: a23 =10, a12 =8.
В =(1 4 5 -6) - матрица-строка, dim B =1´4. - матрица-столбец, dimC=3´1
Пример. - квадратная матрица третьего порядка, n =3
Элементы квадратной матрицы аij при i=j образуют главную диагональ матрицы.
Квадратная матрица, образованная элементами
называется единичной матрицей.
Пример. Единичная матрица 4-го порядка. Нулевая матрица - матрица, у которой все элементы равны нулю. Нулевая матрица может быть любой размерности. Матрица, все элементы которой выше либо ниже главной диагонали равны нулю, называется треугольной матрицей. Пример. А - треугольная матрица.
Сложение Суммой двух матриц А и В называется матрица С, каждый элемент которой сij=aij+bij.
Пример. Свойства операции сложения. 1) коммутативность A + B = B + A 2) ассоциативность (A+B)+ C = A +(B+C)
Пример.
Произведение матриц Произведением матрицы А dim А=m´p и матрицы B dim B=p´n называется матрица C dim C=m´n, каждый элемент которой сij равен «произведению i -той строки матрицы А на j -тый столбец матрицы В».
Свойства операции умножения. - ассоциативность (АВ) С=А (ВС); - дистрибутивность А (В+С)= АВ+АС; - существование нейтрального элемента (единичной матрицы): АЕ=ЕА=А; - связь между операцией транспонирования и произведением матриц: (АВ) Т = ВТАТ. Замечания . 1) Умножение матриц не коммутативно, то есть АВ 2) Обратной операции - деления не существует. 3) Если АВ=ВА, то в этом случае матрицы А и В называются коммутативными.
Dim A =2´3, dim B =3´3.
Определители и их свойства
Свойства определителей 1) При транспонировании матрицы определитель не изменяется, т.е. det A =det(AT) 2) При перестановке двух строк (столбцов) определитель меняет знак на обратный. 3) При круговой перестановке строк (столбцов) определитель не изменяется. 4) Если в определителе есть две одинаковые строки (столбца), то определитель равен 0; если одна из строк (столбцов) матрицы получается из другой строки (столбца) умножением на некоторый множитель, то определитель равен 0. 5) При умножении матрицы порядка n на число l определитель умножается на l n. 6) При умножении одной строки (столбца) на числоl определитель умножается на это число.
Обратная матрица Ранг матрицы
Определение ранга матрицы Пусть А - произвольная матрица. Возьмем k столбцов и k строк матрицы А, где k£ min (m,n). Определение. Минором М матрицы А называется определитель k -го порядка, полученный на пересечении k строк и k столбцов матрицы А. Пример. Дана матрица А.
Максимальный порядок миноров данной матрицы равен четырем.
Рангом матрицы называется наивысший из порядков не равных нулю миноров этой матрицы. Обозначение: rang A или r(A ).
Пример. Дана матрица А.
det A =0, все миноры второго порядка равны 0. Минор 1-го порядка М =
Системы линейных уравнений Определение системы
Пусть дана система m линейных уравнений с n неизвестными.
В матричной форме записи: AX=B, где А -матрица коэффициентов, Х – столбец неизвестных, В – столбец свободных членов.
Решением системы линейных уравнений называется всякий столбец
,
удовлетворяющий матричному уравнению АХ=В.
Классификация систем 1) АХ=О (В =О) - однородная система. 2) АХ=В (В ¹О) - неоднородная система.
Крамеровские системы Неоднородная система линейных уравнений называется крамеровской, если выполнены следующие условия: 1) m = n, т.е. число уравнений равно числу неизвестных; 2) det А ¹0 – определитель матрицы коэффициентов не равен нулю. Иначе: система линейных уравнений крамеровская, если А – квадратная невырожденная матрица. Т.к. А – квадратная матрица, то существует обратная матрица А -1, тогда решение системы дается формулой: Х=А -1 В. Правило Крамера в матричной форме записи:
Здесь Dравен определителю матрицы коэффициентов, D I есть определитель матрицы коэффициентов, в котором на месте i -го столбца стоит столбец свободных членов.
Пример. Решить систему уравнений: 1) Вычисляем det А = D и определители D i:
 
x1 =
1.6.4.Произвольные неоднородные системы
Пусть дана система m линейных уравнений с n неизвестными.
Система называется совместной, если у нее существует хотя бы одно решение.
Теорема Кронекера – Капелли. Для того чтобы система линейных уравнений была совместна (т.е. имела решение), необходимо и достаточно, чтобы rang A =rang (A / B). Теорема о числе решений неоднородной системы: пусть для системы из m уравнений с n неизвестными выполнено условие совместности, т.е. r(A)= r(A / B)= r. Тогда: если r = n, то система имеет единственное решение. Если r < n, то система имеет бесконечное множество решений.
При этом (n - r) - неизвестным придают произвольное значение, они называются свободными неизвестными; r - число базисных неизвестных.
Пример. Решить систему линейных уравнений.
Составим расширенную матрицу: (A / B)= Определим ранги r(A) и r(A / B).
r(A) =r(A / B)=3<4, следовательно, система имеет бесконечное множество решений; n-r =4-3=1 - одна свободная неизвестная. r = 3 - три базисных неизвестных. Т.к. r = 3, то выберем ненулевой минор третьего порядка, который назовем базисным минором.
Т.к. в базисный минор входили коэффициенты при х1, х2, х3, то эти неизвестные будут базисными, оставшаяся х4 - свободной. Перепишем систему в виде: х1- 2 х2- 3 х3 = 2+5 х4 2 х1+х2+ 4 х3= 3 -х4 3 х1- 3 х2+ 8 х3 =-1+2 х4 Полученная система является крамеровской, т.к. определитель матрицы коэффициентов есть ненулевой минор третьего порядка. По правилу Крамера выразим х1, х2, х3 через х4. х1= 30 + 71 х4 х2= -7-15 х4 х3= -14-32 х4 Обозначим х4=С (произвольная константа), тогда общее решение системы имеет вид:
Придавая С различные значения, мы получим бесконечное множество частных решений системы. Например,
Однородные системы Пусть дана однородная система m линейных уравнений с n неизвестными.
Однородная система всегда совместна, т.к. всегда имеет нулевое (тривиальное) решение Х =0. Теорема о решении однородной системы. Для того чтобы однородная система с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы r(A)< n. При m = n условие r(A)< n означает, что определитель матрицы коэффициентов равен нулю.
Пример. Решить систему линейных однородных уравнений.
n=4 – число неизвестных. 1) Вычислим r(A) методом окаймляющих миноров.
Следовательно, r(A)=2. 2) 5 x3+ 3 x4=- 2 x1+ 4 x2 4 x3+ 2 x4=- 3 x1+ 6 x2 x1,x2 -свободные неизвестные, x3,4 -связнные. Выразим x3,x4 через x1, x2 х3 =-2,5 x1+ 5 x2 х4=- 3,5 x1- 7 x2. 3) Обозначим: x1=С1, x2=С2, тогда общее решение системы:
Частные решения:
Замечание. Если однородная система имеет хотя бы одно нетривиальное решение, то она имеет бесконечное множество решений.
Общее решение системы есть формула, которая отражает решения системы как функцию свободных неизвестных.
Векторная алгебра
Понятие вектора
Вектором называется направленный отрезок прямой, то есть отрезок, относительно которого указано, какая из его точек является началом, какая концом.
Вектор можно обозначать Длиной или модулем вектора называется расстояние между началом и концом вектора, обозначают | Единичным вектором называется вектор Нулевым вектором называется вектор, у которого начало совпадает с концом. Обозначается: Нулевой вектор не имеет ни длины, ни направления. Два вектора называются равными, если они имеют равные длины и совпадающие направления. Ортом вектора
Два вектора
- сонаправленными, обозначают: - противоположно направленными, обозначают: Три вектора называются компланарными, если они параллельны одной и той же плоскости. Проекция вектора на ось
Углом между векторами  и и  называется наименьший из двух углов j (0£ j £ p), на который надо повернуть один вектор, чтобы его направление совпало со вторым после приведения этих векторов к общему началу: называется наименьший из двух углов j (0£ j £ p), на который надо повернуть один вектор, чтобы его направление совпало со вторым после приведения этих векторов к общему началу:
Рассмотрим ось l, положительное направление которой задано единичным вектором Проекцией точки А на ось l называется точка пересечения оси l с плоскостью, проходящей через точку А перпендикулярно оси l - точка А1. Рассмотрим произвольный вектор Проекцией вектора
осью  острый, и отрицательное число - острый, и отрицательное число -  , если угол между вектором , если угол между вектором  и осью и осью  - тупой. - тупой.
Обозначается проекция вектора Базис. Координаты вектора
Пусть V – векторное пространство. Базисом в пространстве V называется всякая система векторов Обозначим через V1 – множество векторов на прямой; V2 – множество векторов на плоскости; V3 - множество векторов в пространстве. Базисом в V1 называется любой ненулевой вектор; в V2 – любая пара неколлинеарных векторов; в V3 – любая упорядоченная тройка некомпланарных векторов. Теорема о разложении вектора по базису:Любой вектор можно разложить по базису единственным образом: 1) в V1: 2) в V2: 3) в V3:
2.6. Прямоугольная (декартова) система координат
Системой прямоугольных (декартовых координат) называется совокупность точки O и базиса, обозначаемого 1) 2) 3) тройка векторов Любой вектор
числа х, у, z называются прямоугольными ( декартовыми ) координатами вектора Геометрический смысл координат вектора – координаты вектора есть проекции этого вектора на координатные оси: х= у= z= Cos a, cos b, cos g - называются направляющими косинусами вектора.
Пусть даны точка М1 (х1,у1,z1) и точка М2 (х2,у2,z2), тогда вектор Координаты вектора Модуль вектора
Рассмотрим векторы - если - если
Условие коллинеарности векторов в координатной форме: векторы
Координаты середины отрезка М1М2:
2.7. Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними:
Алгебраические свойства скалярного произведения: 1) 2) 3) ( a 4) ( Геометрические свойства скалярного произведения: 1) 2) Два ненулевых вектора - острый угол, если - тупой угол, если Скалярное произведение в координатах двух векторов
Из определения скалярного произведения вытекают следующие формулы: - косинус угла между векторами - проекция вектора Прямые и плоскости Задание прямой на плоскости
Всякий вектор  , параллельный прямой L, называется направляющим вектором прямойL. , параллельный прямой L, называется направляющим вектором прямойL.
Всякий вектор Прямая на плоскости задается: 1) парой точек этой прямой; 2) точкой и направляющим вектором прямой, тогда множество точек М прямой, проходящей через точку М0 параллельно вектору 3) точкой и нормальным вектором прямой, тогда множество точек М прямой, проходящей через точку М0 ортогонально вектору Задание плоскости в пространстве
Плоскость в пространстве может быть задана: 1) тремя точками плоскости; 2) точкой и нормальным вектором плоскости, тогда множество точек М плоскости, проходящей через точку М0 ортогонально вектору 3) точкой и двумя неколлинеарным векторам Виды уравнений плоскости
1) Общее уравнение плоскости: Ах+By+Cz+D=0, где
2) Уравнение плоскости,проходящей через точку М0 параллельно
двум неколлинеарным векторам
2)
Уравнение плоскости, проходящей через три точки М1 (x1;y1;z1), M2 (x2;y2;z2), M3 (x3,y3,z3):
Это уравнение есть условие компланарности трех векторов Кривые второго порядка Эллипс
Эллипс – множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
При этом не исключается совпадение фокусов эллипса, в этом случае получаем окружность. Пусть точка М (х,у) – некоторая точка плоскости. Обозначим через r1 и r2 расстояния от точки М до точек F1 и F2 соответственно. Согласно определению эллипса равенство: r1+r2=2a является необходимым и достаточным условием расположения точки М (х,у) на данном эллипсе.
Свойства эллипса. 1) Эллипс симметричен относительно осей Ох и Оу и точки О (0;0) – центра эллипса. Точки пересечения эллипса с осями координат А1 (а; 0) и А2 (-а; 0), В1 (0 ;b) и B2 (0 ;-b) называются вершинами эллипса. Отрезки А1А2=2а и В1B2=2b называются соответственно большой и малой осями эллипса. 2) Эллипс содержится внутри прямоугольника |x|£a, | y|£b. В самом деле, из канонического уравнения вытекает, что Отношение расстояния между фокусами к длине большой оси эллипса называется эксцентриситетом эллипса: е=с/а. Учитывая, что b2=a2-c2, получим:
Из этой формулы видно, что эксцентриситет эллипса меньше единицы. Чем больше эксцентриситет эллипса, тем меньше отношение Гипербола Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек плоскости F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
Точки F1 и F2 имеют координаты F1 (c, 0) и F2(-c, 0). Пусть точка М (х,у) – некоторая точка плоскости. Обозначим через r1 и r2 расстояния от точки М до точек F1 и F2 соответственно. Согласно определению гиперболы равенство: |r1-r2|=2a является необходимым и достаточным условием расположения точки М (х,у) на данной гиперболе. Уравнение гиперболы в данной системе координат примет вид:
где b2=c2-a2. Если а=b, то гипербола называется равносторонней. Свойства гиперболы. 1) Гипербола симметрична относительно осей Ох и Оу и точки О (0;0) – центра гиперболы. 2) Гипербола состоит из двух частей, называемых ветвями гиперболы. Точки пересечения гиперболы с осью Ох А1 (а; 0) и А2 (- а; 0) называются вершинами гиперболы. Отрезок А1А2=2а называется действительной осью гиперболы. 3) Прямые Отношение расстояния между фокусами к длине действительной оси эллипса называется эксцентриситетом гиперболы: е=с/а. Учитывая, что b2=с2-а2, получим:
Из этой формулы видно, что эксцентриситет гиперболы больше единицы. Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины угла между ее асимптотами, т.к. отношение Парабола
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.141 (0.24 с.) |









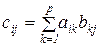
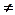 ВА;
ВА;




 =3¹0, следовательно, r(A)=1.
=3¹0, следовательно, r(A)=1.



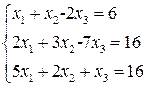


 ; x2 =
; x2 =  ; x3 =
; x3 =  .
. Ответ: решение системы
Ответ: решение системы
 Главную роль в определении совместности системы играет ранг матрицы. Составим матрицу (А / В), которая называется расширенной матрицей.
Главную роль в определении совместности системы играет ранг матрицы. Составим матрицу (А / В), которая называется расширенной матрицей.




 .
.


 выберем в качестве базисного, тогда система уравнений запишется в виде:
выберем в качестве базисного, тогда система уравнений запишется в виде:
 (c1= 0 ,c2= 1 ) =
(c1= 0 ,c2= 1 ) = 

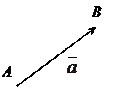
 , где А – начало вектора, В - его конец, или
, где А – начало вектора, В - его конец, или  , модуль которого равен единице: |
, модуль которого равен единице: |  .
. . Обозначается:
. Обозначается: .
.
 .
.
 и вычисляется по формуле:
и вычисляется по формуле:  .
. , которая линейно независима и полна (т. е. всякий вектор пространства можно выразить через данную систему векторов).
, которая линейно независима и полна (т. е. всякий вектор пространства можно выразить через данную систему векторов). ;
;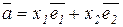 ;
; .
. и удовлетворяющего условиям:
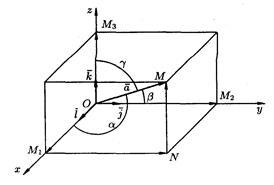
и удовлетворяющего условиям: =1;
=1; ,
,
 ,
, ;
; ;
; .
. .
. .
. , равный расстоянию между точками М1 и М2, находится по формуле:
, равный расстоянию между точками М1 и М2, находится по формуле: .
.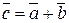 , то
, то  (ха+хb; уа+уb; zа+zb);
(ха+хb; уа+уb; zа+zb); , то
, то  .
. .
. .
.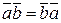 - свойство коммутативности;
- свойство коммутативности; - скалярное произведение вектора на себя равно квадрату модуля вектора;
- скалярное произведение вектора на себя равно квадрату модуля вектора; ) – свойство ассоциативности;
) – свойство ассоциативности; +
+  - свойство дистрибутивности.
- свойство дистрибутивности.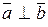 тогда и только тогда, когда
тогда и только тогда, когда  ;
; .
.
 , ортогональный прямой L, называется нормальным вектором прямой L.
, ортогональный прямой L, называется нормальным вектором прямой L. .
. , будет удовлетворять условию
, будет удовлетворять условию  .
.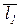 ,
,  , тогда множество точек М плоскости будет удовлетворять условию, что векторы
, тогда множество точек М плоскости будет удовлетворять условию, что векторы  ,
, 
 .
.
 .
. .
.
 - каноническое уравнение эллипса.
- каноническое уравнение эллипса. . Эти неравенства эквивалентны неравенствам |x|£a, | y|£b.
. Эти неравенства эквивалентны неравенствам |x|£a, | y|£b. .
. малой полуоси эллипса b к его большой полуоси а, и значит, тем более сплющенным будет эллипс.
малой полуоси эллипса b к его большой полуоси а, и значит, тем более сплющенным будет эллипс.
 - каноническое уравнение гиперболы,
- каноническое уравнение гиперболы, и
и  называются асимптотами гиперболы ( ветви гиперболы неограниченно приближаются к этим прямым).
называются асимптотами гиперболы ( ветви гиперболы неограниченно приближаются к этим прямым). .
.


