
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Элементы специальной теории относительности
4.1. Преобразования Галилея. Механический принцип относительности
Из определения инерциальной системы отсчета (это та система отсчета, по отношению к которой выполняется закон инерции - первый закон Ньютона: материальная точка, на которую не действуют другие тела (изолированная точка), покоится, либо движется равномерно и прямолинейно) следует, что во всех инерциальных системах отсчета ускорение изолированной материальной точки должно быть равно нулю. Последнее позволяет установить, как должна двигаться относительно инерциальной системы отсчета какая-либо другая система, для того, чтобы она также была инерциальной. Оказывается, что две инерциальные системы отсчета могут двигаться друг относительно друга только поступательно и притом равномерно и прямолинейно.
Рассмотрим две инерциальных системы отсчета: систему XYZ, которую будем условно считать неподвижной, и подвижную систему отсчета X/Y/Z/, скорость поступательного движения которой равна  Примем для упрощения задачи, что в начальный момент времени t = 0 начала отсчета O и O’ обеих систем координат и соответствующие оси совпадали. В произвольный момент времени t ¹ 0 взаимное расположение этих систем имеет вид, изображенный на рис. 4.1. Скорость подвижной системы координат Примем для упрощения задачи, что в начальный момент времени t = 0 начала отсчета O и O’ обеих систем координат и соответствующие оси совпадали. В произвольный момент времени t ¹ 0 взаимное расположение этих систем имеет вид, изображенный на рис. 4.1. Скорость подвижной системы координат  направлена вдоль прямой OO/, радиус-вектор, проведенный из O в O/, можно определить как: направлена вдоль прямой OO/, радиус-вектор, проведенный из O в O/, можно определить как: 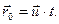
Положение произвольной точки М в неподвижной и подвижной системах отсчета определяются радиус-векторами
В проекциях на оси координат уравнение (4.1.1,а) можно записать в следующем виде:
В классической ньютоновской механике принимают, что ход времени не зависит от относительного движения системы отсчета. Поэтому систему уравнений (4.1.1,б) можно дополнить еще одним: t = t/. Выражения (4.1.1,а) и (4.1.1,б) называют преобразованием Галилея. Дифференцируя уравнение (4.1.1,а) по времени, и учитывая, что
Первое уравнение в (4.1.2) называют законом сложения скоростей в классической механике. Если точка М не подвержена действию других тел, то
В общем случае силы взаимодействия между телами зависят от взаимного расположения этих тел и от скорости их движения друг относительно друга. Из соотношений (4.1.1,а) и (4.1.2) следует, что для любых двух материальных точек 1 и 2 можно получить:
Из уравнений (4.1.2) и (4.1.3) для инерциальных систем отсчета получим, что Итак, уравнения Ньютона для материальной точки, а также для произвольных систем материальных точек одинаковы во всех инерциальных системах отсчета – инвариантны по отношению к преобразованию Галилея. Этот результат называется «механическим принципом относительности» (принципом относительности Галилея) и часто формулируется следующим образом: равномерное и прямолинейное замкнутой системы движение (относительно какой-либо инерциальной системы отсчета) не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Другими словами, нельзя выделить из множества инерциальных систем отсчета какую-то «главную» инерциальную систему отсчета, которая обладала бы какими-либо преимуществами перед другими (так что движение тел относительно нее можно было бы рассматривать как «абсолютное движение», а покой – как «абсолютный покой»).
4.2. Частная (специальная) теория относительности Эйнштейна. Преобразования Лоренца. Следствия из преобразования Лоренца Для описания движения тел со скоростями (u) сравнимыми со скоростью света (с) используется релятивистская механика, учитывающая требования специальной теории относительности.
Основоположником теории относительности Эйнштейном (1905 г.) был предложен принципиально новый подход к электродинамике движущихся тел. Проанализировав огромный экспериментальный материал, Эйнштейн выбрал два наиболее бесспорных положения и построил на их основе свою теорию. Частная (специальная) теория относительности применима к инерциальным система отсчета и основана на двух постулатах Эйнштейна: 1) Все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. 2) Скорость света в пустоте одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света. Принцип относительности (1) и принцип постоянства скорости света (2) образуют основу специальной теории относительности, которая представляет собой по существу физическую теорию пространства и времени. В классической механике пространство и время рассматривались независимо друг от друга. Ньютон считал, что существует абсолютное пространство и абсолютное время. Абсолютное пространство определялось или как безотносительное к чему-либо внешнему вместилище вещей, остающееся всегда одинаковым и неподвижным. О времени Ньютон писал: «Абсолютное, истинное или математическое время само по себе и в силу своей внутренней природы течет равномерно, безотносительно к чему-либо внешнему». В соответствии с этим считалось совершенно очевидным, что два события, одновременные в какой-либо системе отсчета, будут одновременными и во всех остальных системах отсчета. Однако легко убедиться в том, что последнее утверждение находится в противоречии с принципом постоянства скорости света. Для иллюстрации этого вывода рассмотрим две инерциальные системы отсчета: К (с координатами х, у, z) и К ' (с координатами x ', у ', z '), движущуюся относительно К (вдоль оси х) со скоростью υ=const (рис. 4.2).
Пусть в начальный момент времени t = t ' = 0, когда начала координат О и О' совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одна и та же и равна с. Поэтому если за время t в системе К сигнал дойдет до некоторой точки А (рис. 4.2), пройдя расстояние
то в системе К ' координата светового импульса в момент достижения точки А
где t ' — время прохождения светового импульса от начала координат до точки А в системе К '. Вычитая (4.2.1, а) из (4.2.1, б), получаем х' - х = c (t ' - t). Так как х' ≠ х (система К ' перемещается по отношению к системе К), то t ≠ t ', т. е. отсчет времени в системах К и К ' различен — отсчет времени имеет относительный характер (в классической физике считается, что время во всех инерциальных системах отсчета течет одинаково, т. е. t = t '). Эйнштейн показал, что в теории относительности классические преобразования Галилея, описывающие переход от одной инерциальной системы отсчета к другой
заменяются преобразованиями Лоренца, удовлетворяющими постулатам Эйнштейна (формулы представлены для случая, когда К ' движется относительно К со скоростью υ вдоль оси х). Эти преобразования предложены Х. А. Лоренцем в 1904 г., еще до появления теории относительности, как преобразования, относительно которых уравнения Максвелла инвариантны.
Преобразования Лоренца имеют вид:
Из преобразований Лоренца вытекает, что при малых скоростях (по сравнению со скоростью с), т. е. когда Из преобразований Лоренца следует очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках преобразований Галилея эти величины считались абсолютными, не изменяющимися при переходе от системы к системе. Следствия из преобразования Лоренца
Из преобразования Лоренца вытекают ряд необычных с точки зрения классической механики следствий:
1. Одновременность событий в разных системах отсчета. Пусть в системе К в точках с координатами x 1 и x 2 происходят одновременно два события в момент времени t 1 = t 2 = b. Согласно (4.2.2) в системе К/ этим событиям будут соответствовать координаты:
Таким образом, в случае, если упомянутые события в системе К происходят в одном и том же месте пространства (x 1 = x 2), то они будут совпадать в пространстве (x 1/ = x 2/) и во времени (t1/ = t2/) также и в системе К/. Если же события в К пространственно разобщены (x 1 ¹ x 2), то и в К’ они также окажутся разобщенными (x 1/ ¹ x 2/), но не будут одновременными (t1/ ¹ t2/). Знак t2/ - t1/ определяется знаком υ ×(x 1 – x 2). Следовательно в разных системах К (при различных значениях скорости движения подвижной системы координат К/ – υ) разность t2/ - t1/ будет различной по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 предшествует событию 2, в других – наоборот. Заметим, что сказанное относится лишь к событиям, между которыми отсутствует причинно-следственная связь. Причинно связанные события ни в одной системе не будут одновременными, и причина всегда предшествует следствию.
2. Длина тел в разных системах отсчета.
Рассмотрим стержень, расположенный вдоль оси OX, и покоящийся относительно системы К/ (см. рис. 4.3).
Длина стержня в системе К/ равна l 0 = x 2/ – x 1/, где x 1/ и x 2/ - не изменяющиеся со временем t / координаты концов стержня. Относительно системы К стержень движется со скоростью υ. Найдем координаты концов стержня x 1 и x 2 в один и тот же момент времени t 1 = t 2 = b в системе K. Пусть l = x 2 – x 1. Используя выражения (4.2.2), получим формулы преобразования для двух координат концов стержня, и, соответственно, длины стержня, определяемой как разность координат:
Таким образом, длина стержня l,измеренная в системе, относительно которой он движется, оказывается меньше длины l 0, измеренной в системе, относительно которой стержень покоится. В направлении осей OY и OZ радиусы стержня одинаковы во всех системах отсчета. Итак, у движущихся тел размеры их в направлении движения сокращаются тем больше, чем больше скорость движения. Это явление называется лоренцевым сокращением.
3. Длительность событий в разных системах отсчета. Пусть в точке, неподвижной относительно системы К/, происходит событие, длящееся время D t 0 = t 2/ – t 1/. Началу события соответствует в системе К/ координата x 1/ = a и момент времени t 1/, концу события – x 2/ = a и t 2/, соответственно. Относительно системы К рассматриваемая точка перемещается. Согласно (4.2.2), началу и концу события соответствуют в системе К:
В (4.2.5) D t 0 – длительность события, определенное по часам движущимся вместе с телом. D t – временной интервал, измеренный по часам системы, относительно которой тело движется. Из соотношения (4.2.5) следует, что D t 0 < D t. Таким образом, движущиеся часы идут медленнее, чем покоящиеся. 4. Интервал. Какое - либо событие можно охарактеризовать местом, где оно произошло (x, y, z) и временем t. Введем четырехмерное пространство, на координатных осях которого будем откладывать пространственные координаты и время. В этом пространстве событие изображается точкой, которую принято называть мировой точкой. Всякой частице в этом пространстве будет соответствовать некоторая линия, называемой мировой. Пусть одно событие имеет координаты (x 1, y 1, z 1, t 1), другое (x 2, y 2, z 2, t 2). Величину
называют интервалом между соответствующими событиями. Введя расстояние между точками обычного трехмерного пространства, в которых произошли оба события:
Легко убедиться, что величина S является инвариантом. Действительно, запишем интервал в системе К:
В системе К’:
Согласно соотношению (4.2.2):
После подстановки последних выражений в соотношение для S12’ получим, что:
то есть
Таким образом, интервал (4.2.8) является инвариантом по отношению к переходу от одной инерциальной системы отсчета к другой. Согласно (4.2.5), собственное время события, т.е. время, измеренное по часам, движущимся относительно инерциальной системы отсчета
Преобразуем выражение, учитывая, что t=t2-t1=Dt,
тогда
Промежуток собственного времени пропорционален интервалу между событиями. Поскольку S12 - интервал между событиями является инвариантом, т.е. одинаков во всех инерциальных системах отсчета, то и собственное время так же является инвариантом. Таким образом, собственное время не зависит от того, в какой системе отсчета наблюдается движение данного тела.
5. Релятивистский закон сложения скоростей. Рассмотрим движение материальной точки. В неподвижной системе координат К положение точки в момент времени t определяется координатами x, y, z. Выражения
представляют собой проекции на оси OX, OY и OZ вектора скорости точки относительно системы отсчета К. В К/ положение точки в момент времени t / определяется координатами x /, y / и z /, а проекции вектора скорости этой же точки относительно системы К/ на оси O/X/, O/Y/ и O/Z/:
Из уравнений (4.2.2) можно получить:
Разделив
Первое соотношение в (4.2.9) называют релятивистским законом сложения скоростей. В случае, когда скорость объекта много меньше скорости света υ «c, то выражение (4.2.9) преобразуется в выражение (4.1.2). Если тело движется параллельно оси OX, то его скорость u относительно системы К совпадает с ux (uy /=0 и uz /=0), а скорость u/ относительно К/ – с ux (uy = 0 и uz = 0). При этом закон сложения скоростей примет вид:
Пусть u/ = c. В этом случае
6. Релятивистский импульс
Выражение, обеспечивающее инвариантность закона сохранения импульса, может быть получено, если вместо времени t подставить собственное время τ. Тогда
7. Релятивистское выражение для энергии В релятивистской механике справедливым остается выражение
Это означает, что Получим выражение для кинетической энергии. Поскольку dEk = dA и dEk = υ · p · dt, dA = F · ds, то
Отсюда следует, что E0 = mc2 является энергией покоя. Энергия и импульс в релятивистской механике не сохраняются.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.068 с.) |

 и
и  (см. рис. 4.1), причем
(см. рис. 4.1), причем

 найдем соотношение между скоростями и ускорениями точки М относительно обеих систем:
найдем соотношение между скоростями и ускорениями точки М относительно обеих систем:

 Так как
Так как  (из (4.1.2)), рассматриваемая нами подвижная система действительно является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
(из (4.1.2)), рассматриваемая нами подвижная система действительно является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится. и
и  Следовательно, силы, действующие на данную материальную точку (или тело) со стороны других тел, одинаковы во всех инерциальных системах отсчета, то есть
Следовательно, силы, действующие на данную материальную точку (или тело) со стороны других тел, одинаковы во всех инерциальных системах отсчета, то есть
 Таким образом, из приведенного выше материала следует, что инвариантами (инвариант – физическая величина, которая не зависит от выбора системы отсчета и является одинаковой во всех инерциальных системах) в механике Ньютона являются: 1) интервал времени (D t = t 2 – t 1), 2) длина отрезка (
Таким образом, из приведенного выше материала следует, что инвариантами (инвариант – физическая величина, которая не зависит от выбора системы отсчета и является одинаковой во всех инерциальных системах) в механике Ньютона являются: 1) интервал времени (D t = t 2 – t 1), 2) длина отрезка ( ), 3) масса (m), а также производных от них: 4) ускорение (
), 3) масса (m), а также производных от них: 4) ускорение ( ) и сила (
) и сила ( ).
).



 (4.2.2).
(4.2.2).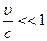 , они переходят в классические преобразования Галилея (в этом заключается суть принципа соответствия), которые являются, следовательно, предельным случаем преобразований Лоренца. При υ > с выражение (4.2.2) для х, t, x ', t ' теряют физический смысл (становятся мнимыми). Это находится, в свою очередь, в соответствии с тем, что движение со скоростью, большей скорости распространения света в вакууме, невозможно.
, они переходят в классические преобразования Галилея (в этом заключается суть принципа соответствия), которые являются, следовательно, предельным случаем преобразований Лоренца. При υ > с выражение (4.2.2) для х, t, x ', t ' теряют физический смысл (становятся мнимыми). Это находится, в свою очередь, в соответствии с тем, что движение со скоростью, большей скорости распространения света в вакууме, невозможно.

 и
и  или
или
 и
и  . Длительность события
. Длительность события  , или
, или

 , и временной интервал t 12 = t 2 – t 1, выражение (4.2.6) можно представить в виде:
, и временной интервал t 12 = t 2 – t 1, выражение (4.2.6) можно представить в виде:



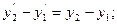




 .
. :
: ,
, .
.








 , получим следующие соотношения:
, получим следующие соотношения:

 Последний результат не является удивительным, поскольку в основе преобразования Лоренца лежит утверждение, что скорость света одинакова во всех системах отсчета. Приняв u/ = υ= c, получим для u также значение равное с. Таким образом, если складываемые скорости u/ и υ не превышают с, то и результирующая скорость u не может превысить с.
Последний результат не является удивительным, поскольку в основе преобразования Лоренца лежит утверждение, что скорость света одинакова во всех системах отсчета. Приняв u/ = υ= c, получим для u также значение равное с. Таким образом, если складываемые скорости u/ и υ не превышают с, то и результирующая скорость u не может превысить с. .
.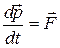 .
. . Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.
. Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны. .
.


