
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование случайных процессов ⇐ ПредыдущаяСтр 6 из 6
Краткие сведения К числу случайных процессов, изучаемых методом имитационного моделирования (методом Монте-Карло) относятся, в частности, процессы, связанные с формированием и обслуживанием очередей (так называемые процессы массового обслуживания). Простейшая задача данного класса такова. Имеется система массового обслуживания с одним узлом обслуживания (магазин с одним продавцом, ремонтная зона в автохозяйстве, травмопункт с одним врачом, телефонная станция с одним входом, сервер с одним входным каналом и т.д.). К услугам системы клиенты прибегают случайным образом (с заданной функцией распределения отрезков времени между приходами). Если система свободна, то начинает обслуживать клиента сразу, иначе ставит его в очередь. Длительность обслуживания каждого клиента - случайная величина с известным законом распределения. В ходе решения данной задачи требуется дать ответ на вопросы типа «какова функция распределения вероятностей времени ожидания клиента в очереди?» «каково время простоя системы в ожидании клиентов?», «если сами эти функции определять сложно, то каковы их наиболее важные характеристики (т.е. математическое ожидание, дисперсия и т.д.)?». Основа этой задачи - случайный процесс прихода клиентов в систему обслуживания. Промежутки между приходами любой последовательной пары клиентов - независимые случайные события, распределенные по некоторому закону. Реальный характер этого закона может быть установлен лишь путем многочисленных наблюдений; в качестве простейшей модельной функции плотности вероятности можно взять равновероятное распределение в диапазоне времени от 0 до некоторого Т - максимально возможного промежутка между приходами двух последовательных покупателей. При этом распределении вероятность того, что между приходами двух покупателей пройдет 1 минута, 3 минуты или 8 минут, одинакова (если Т > 8 мин). Такое распределение, конечно, малореалистично; реально для большинства процессов массового обслуживания функция распределения растет от t = 0, имеет при некотором значении t = τ максимум и быстро спадает при больших t, т.е. имеет вид, изображенный на рис. 7.6. Можно, конечно, подобрать немало элементарных функций, имеющих качественно такой вид. В теории массового обслуживания широко используется семейство функций Пуассона
где λ - некоторая постоянная, п - произвольное целое. Функции (35) имеют максимум при х = п/λ и нормированы. Второй случайный процесс в этой задаче, никак не связанный с первым, определяется последовательностью случайных событий - длительностями обслуживания каждого из покупателей. Распределение вероятностей длительности обслуживания имеет тот же качественный вид, что и в предыдущем случае. Для примера в таблице в колонке А записаны случайные числа - промежутки между приходами клиентов (в минутах), в колонке В - случайные числа - длительности обслуживания (в минутах). Для определенности взято аmax = 10 и bmax = 5.
Рис..6. Схематическое изображение плотности вероятности распределения времени между появлениями клиентов в системе массового обслуживания Из этой короткой таблицы, разумеется, невозможно установить, какие законы распределения приняты для величин А и В. Остальные колонки предусмотрены для удобства анализа; входящие в них числа находятся путем элементарного расчета. В колонке С представлено условное время прихода клиента; D - момент начала обслуживания; Е - момент конца обслуживания; F - длительность времени, проведенного клиентом в системе в целом; G - время, проведенное в очереди в ожидании обслуживания; Н - время, проведенное системой в ожидании клиентов (если их нет). Таблицу удобно заполнять по горизонтали, переходя от строчки к строчке. Так как начало обслуживания очередного клиента определяется либо временем его прихода, если система не занята, либо временем ухода предыдущего клиента, приведем для удобства соответствующие формулы (в них i = 1, 2, 3,...): с1 = 0, сi+1 = сi + аi+1; d1 = 0, di+1 = max(ci+l, ei); (36a) e1 = b1 ei = di + bi; fi = ei + ci; g1 = 0; gi+1 = fi+1 + bi+1 h1= 0; hi+1 = di+1 - ei (36б) Таким образом, при данных случайных наборах чисел в колонках А и В клиентам приходилось стоять в очереди (колонка G), и система простаивала в ожидании клиента (колонка Н).
При моделировании систем такого вида прежде всего возникает вопрос, какое среднее время приходится стоять в очереди? Ответить на него, кажется, несложно - надо найти
в некоторой серии испытаний. Аналогично можно найти среднее значение величины h. Труднее ответить на вопрос о достоверности полученных результатов; для этого надо провести несколько серий испытаний и использовать стандартные методы математической статистики (часто уместна обработка с помощью распределения Стьюдента). Более сложный вопрос - каково распределение случайных величин G и Н при заданных распределениях случайных величин A и В? Качественный ответ на него можно попытаться получить, построив соответствующие гистограммы по результатам моделирования. Затем делается некоторая гипотеза о виде распределения и используются один или несколько статистических критериев проверки достоверности этой гипотезы. Располагая функцией распределения (пусть даже эмпирической, но достаточно надежной), можно ответить на любой вопрос о характере процесса ожидания в очереди. Например: какова вероятность прождать дольше т минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямыми х = т и y=0 площади всей фигуры. Контрольные вопросы 1. Что такое «случайный процесс»? 2. Каковы принципы компьютерного генерирования равномерно распределенных случайных чисел? 3. Как можно получить последовательность случайных чисел с пуассоновским законом распределения? 4. Что такое «система массового обслуживания»? Приведите примеры. 5. В чем заключается метод Монте-Карло вычисления площадей плоских фигур? объемов тел? 6. Какие примеры случайных процессов Вы можете привести? Темы для рефератов 1. Принципы компьютерной генерации последовательностей случайных чисел и статистические критерии определения свойств последовательностей. 2. Методы статистической обработки результатов, полученных при компьютерном моделировании случайных процессов. Тема семинарских занятий Получение последовательностей случайных чисел с заданным законом распределения. Лабораторная работа Общие рекомендации 1. При выполнении данной работы необходима генерация длинных последовательностей псевдослучайных чисел с заданным законом распределения вероятностей. Ее можно основывать на стандартном датчике равномерно распределенных случайных чисел, встроенном в применяемую систему программирования, с использованием одной из процедур пересчета данной последовательности в последовательность с нужным законом распределения (например, процедуру «отбор - отказ»). 2. Одна из центральных задач при моделировании случайных процессов - нахождение характеристик случайных величин, являющихся объектом моделирования. Главная такая характеристика - функция распределения. Ее вид можно качественно оценить по гистограмме, построенной в ходе моделирования, а гипотезу о функциональной форме проверить с помощью одного из стандартных критериев, используемых в математической статистике (например, критерия %2). Однако это не всегда целесообразно, особенно если в задаче требуется определить лишь некоторые характеристики случайной величины - чаще всего среднее значение и дисперсию. Их можно найти без моделирования самой функции распределения. При этом статистическая оценка достоверности результатов является обязательной.
3. Результаты моделирования уместно выводить на экран компьютера в следующем виде: в виде таблиц значений рассчитываемой величины (как правило, в нескольких выборках), в виде гистограмм распределения случайных величин, построенных в ходе моделирования. 4. Целесообразно там, где это возможно, сопровождать имитационное моделирование визуальным отображением соответствующего процесса на экране компьютера (процесс формирования очереди, рождение и исчезновение объектов в задачах моделирования популяций и т.д.). Примерное время выполнения 16 часов. Задание к лабораторной работе Произвести имитационное моделирование указанного случайного процесса и оценить достоверность полученных результатов, пользуясь статистическими критериями. Варианты заданий Вариант 1 Провести моделирование очереди в магазине с одним продавцом при равновероятных законах распределения описанных выше случайных величин: прихода покупателей и длительности обслуживания (при некотором фиксированном наборе параметров). Получить устойчивые характеристики: средние значения ожидания в очереди покупателем и простой продавца в ожидании прихода покупателей. Оценить их достоверность. Оценить характер функции распределения величин g и h. Вариант 2 Провести то же моделирование при пуассоновских законах распределения вероятностей входных событий: прихода покупателей и длительности обслуживания (при некотором фиксированном наборе параметров). Вариант 3 Провести то же моделирование при нормальном законе распределения вероятностей входных событий: прихода покупателей и длительности обслуживания (при некотором фиксированном наборе параметров). Вариант 4 В рассмотренной выше системе может возникнуть критическая ситуация, когда очередь неограниченно растет со временем. В самом деле, если покупатели заходят в магазин очень часто (или продавец работает слишком медленно), очередь начинает расти, и в рассматриваемой системе с конечным временем обслуживания наступит кризис. Построить зависимость между величинами (amax, bmax), отражающую границу указанной критической ситуации, при равновероятном распределении входных событий.
Вариант 5 На междугородней телефонной станции две телефонистки обслуживают общую очередь заказов. Очередной заказ обслуживает та телефонистка, которая первой освободилась. Если обе в момент поступления заказа заняты, то звонок аннулируется и требуется звонить снова. Смоделировать процесс, считая входные потоки пуассоновскими. Вариант 6 Смоделировать ситуацию, описанную в предыдущем варианте, но считать, что, если в момент попытки сделать заказ обе телефонистки заняты, формируется очередь. Вариант 7 Пусть на телефонной станции с одним входом используется обычная система: если абонент занят, то очередь не формируется и надо звонить снова. Смоделировать ситуацию: три абонента пытаются дозвониться до одного и того же владельца номера и в случае успеха разговаривают с ним некоторое (случайное по длительности) время. Какова вероятность того, что некто, пытающийся дозвониться, не сможет сделать это за определенное время Т? Вариант 8 Смоделировать ситуацию, описанную в предыдущем варианте, но считать, что, если в момент попытки связаться телефон абонента занят, формируется очередь. Вариант 9 На травмопункте работает один врач. Длительность лечения больного и промежутки времени между поступлениями больных - случайные величины, распределенные по пуассоновскому закону. По тяжести травм больные делятся на три категории, поступление больного любой категории - случайное событие с равновероятным распределением. Врач вначале занимается больными с максимально тяжелыми травмами (в порядке их поступления), затем, если таковых нет, - больными с травмами средней тяжести (в порядке их поступления) и лишь затем - больными с легкими травмами. Смоделировать процесс и оценить средние времена ожидания в очереди больных каждой из категорий. Вариант 10 Смоделировать ситуацию, описанную в предыдущем варианте, при условии, что в травмопункте работают два врача, а больные делятся не на три, а на две категории. Вариант 11 Одна ткачиха обслуживает группу станков, осуществляя по мере необходимости краткосрочное вмешательство, длительность которого - случайная величина. Какова вероятность простоя сразу двух станков? Как велико среднее время простоя одного станка? Вариант 12 Смоделировать ситуацию, описанную в предыдущем варианте, если группу станков совместно обслуживают две ткачихи. Вариант 13 В городском автохозяйстве две ремонтные зоны. Одна - обслуживает ремонты краткой и средней продолжительности, другая - средней и долгой (т.е. среднесрочный ремонт может осуществлять каждая из зон). По мере поломок в автохозяйство доставляют транспорт; промежуток времени между доставками - случайная пуассоновская величина. Продолжительность ремонта - случайная величина с нормальным законом распределения. Смоделировать описанную систему. Каковы средние времена ожидания в очереди транспорта, требующего соответственно краткосрочного, среднесрочного и длительного ремонта?
Вариант 14 Реализовать имитационную модель статистического моделирования для решения задачи Бюффона (XVIII в.). Автор аналитически нашел, что если на поле, разграфленное параллельными прямыми, расстояние между которыми L, бросается наугад игла длиной l, то вероятность того, что игла пересечет хотя бы одну прямую, определяется формулой Эта задача дала способ имитационному определению числа п. Действительно, если L = 2l, то Вариант 15 Разработать модель случайного одномерного блуждания (модель «пьяницы»). Блуждание задается по правилу: если случайное число из отрезка [0,1] меньше 0,5, то делается шаг вправо на расстояние h, в противном случае - влево. Распределение случайных чисел принять равновероятным. Решить задачу: какова вероятность при таком блуждании удалиться от начальной точки на п шагов? Вариант 16 В условиях задачи из предыдущего варианта получить ответ на вопрос: какова вероятность «пьянице» вернуться через п шагов в начальную точку? Вариант 17 Точка хаотически блуждает на плоскости по узлам квадратной сетки с возможностью делать с равной вероятностью шаги влево-вправо-вверх-вниз на фиксированный (за один ход) шаг. Движение происходит в замкнутом прямоугольном объеме, и при соприкосновении со стенкой происходит зеркальное отражение от нее. Ответить в ходе моделирования на вопрос: как связана частота посещения каждого узла с расстоянием от него до того узла, из которого начинается движение. Вариант 18 Смоделировать ту же ситуацию, что и в задании к варианту 17, при условии неограниченной области блуждания и ответить на заданный вопрос. Вариант 19 Смоделировать полет пчелы. На плоскости (поляне) случайным образом растут медоносные растения с заданной концентрацией (на 1 м2). В центре - улей, из которого вылетает пчела. Пчела может долететь от одного растения до любого другого растения, но вероятность выбора монотонно уменьшается с увеличением расстояния между растениями (по некоторому закону). Какова вероятность посещения пчелой конкретного заданного растения за заданное количество элементарных перелетов? Вариант 20 Реализовать модель плоского броуновского движения п частиц в прямоугольнике. Частицы считать шариками конечного размера. Удары частиц друг о друга и о стенки моделировать как абсолютно упругие. Определить в этой модели зависимость давления газа на стенки от числа частиц. Вариант 21 Разработать в деталях и реализовать модель перемешивания (диффузии) газов в замкнутом сосуде. В начальный момент времени каждый газ занимает половину сосуда. Изучить с помощью этой модели зависимость скорости диффузии от различных входных параметров. Вариант 22 Реализовать имитационную модель системы «хищник - жертва» по следующей схеме. «Остров» размером 20x20 заселен дикими кроликами, волками и волчицами. Имеется по несколько представителей каждого вида. Кролики в каждый момент времени с одинаковой вероятностью 1/9 передвигаются в один из восьми соседних квадратов (за исключением участков, ограниченных береговой линией) или просто сидят неподвижно. Каждый кролик с вероятностью 0,2 превращается в двух кроликов. Каждая волчица передвигается случайным образом, пока в одном из соседних восьми квадратов не окажется кролик, за которым она охотится. Если волчица и кролик оказываются в одном квадрате, волчица съедает кролика и получает одно очко. В противном случае она теряет 0,1 очка. Волки и волчицы с нулевым количеством очков умирают. В начальный момент времени все волки и волчицы имеют 1 очко. Волк ведет себя подобно волчице до тех пор, пока в соседних квадратах не исчезнут все кролики; тогда, если волчица находится в одном из восьми близлежащих квадратов, волк гонится за ней. Если волк и волчица окажутся в одном квадрате и там нет кролика, которого можно съесть, они производят потомство случайного пола. Пронаблюдать за изменением популяции в течение некоторого периода времени. Проследить, как сказываются на эволюции популяций изменения параметров модели. Вариант 23 Промоделировать процесс распространения инфекции стригущего лишая по участку кожи размером п x п (п - нечетное) клеток. Предполагается, что исходной зараженной клеткой кожи является центральная. В каждый интервал времени пораженная инфекцией клетка может с вероятностью 0,5 заразить любую из соседних здоровых клеток. По прошествии шести единиц времени зараженная клетка становится невосприимчивой к инфекции, возникший иммунитет действует в течение последующих четырех единиц времени, а затем клетка оказывается здоровой. В ходе моделирования описанного процесса выдавать текущее состояние моделируемого участка кожи в каждом интервале времени, отмечая зараженные, невосприимчивые к инфекции и здоровые клетки. Проследить, как сказываются на результатах моделирования изменение размеров поля и вероятность заражения. Вариант 24 Разработать в деталях и реализовать модель распространения загрязняющих окружающую среду частиц вещества, испускаемых в атмосферу заводской трубой (например, золы, получающейся после сжигания угля на электростанции). Считать движение частицы состоящим из двух компонент: в горизонтальной плоскости - под влиянием случайных порывов ветра, в вертикальном - под действием силы тяжести. Дополнительная литература 1. Бейли Н. Статистические методы в биологии: Пер. с англ. - М.: ИЛ, 1962. 2. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. - М.: Наука, 1966. 3. Саати Т. Элементы теории массового обслуживания и ее приложения: Пер. с англ. - М.: Сов. радио, 1991. 4. Шеннон Р. Имитационное моделирование систем - искусство и наука: Пер. с англ. - М.: Мир, 1978. Тесты к главе 7
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.254.0 (0.057 с.) |
 , (35)
, (35)
 (37)
(37)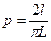 .
. . В ходе моделирования выполнить этот расчет.
. В ходе моделирования выполнить этот расчет.


