
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение удельного сопротивления проводникаСтр 1 из 2Следующая ⇒
Методические УКАЗАНИЯ к лабораторным работам по дисциплине "МЕХАНИКА" (для студентов специальностей "Физика",
У Т В Е Р Ж Д Е Н О на заседании кафедры физики. Протокол № 14 от 03.06.04 Луганск 2004
УДК 530.1
Методические УКАЗАНИЯ к лабораторным работам по дисциплине "МЕХАНИКА" (для студентов специальностей "Физика", "Прикладная физика")
Содержат материал по методике выполнения лабораторных работ по дисциплине "Механика", организации самостоятельной работы и рекомендации по обработке результатов измерений и оформлению отчетов.
Составители: Р.Т. Савченко, ст. преп. В. С Савченко., ст. преп. Г. О. Войтенко, инж.
Ответственный за выпуск П.И. Голубничий, проф.
Рецензент П.И. Голубничий, проф.
1. ПРИБОРНЫЙ СЕМИНАР Лабораторная работа 1 ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКА Цель работы: научиться проводить измерение физических величин, правильно оформлять результаты измерений и расчетов, оценивать погрешности. Приборы и материалы: вольтметр, амперметр, штангенциркуль, шкала определения длины отрезка измеряемого провода. Экспериментальная установка и методика проведения измерений
Перед работой при помощи переключателя вида работ, находящегося на лицевой части прибора, избирается вид работы ("МОСТ"). Передвижением подвижного кронштейна устанавливается необходимая длина провода (примерно 0,7 всей длины провода) и при помощи потенциометра ("РЕГУЛЯЦИЯ ТОКА") проводятся измерения напряжения и силы тока.
Расчетные формулы Сопротивление проводника определяется по известной формуле:
где Т а б л и ц а 1
Т а б л и ц а 2
10. Записать вывод о проделанной работе.
Контрольные вопросы
1. Выведете рабочую формулу для расчёта удельного сопротивления. 2. Что такое абсолютная погрешность? 3. Что такое относительная погрешность? 4. Как определяется абсолютная погрешность длины при прямых измерениях? 5. Как определяется абсолютная погрешность диаметра при прямых измерениях? 6. Как определяется абсолютная погрешность при измерении физических величин стрелочными приборами? 7. Как использовать график 8. Как рассчитывается относительная погрешность при косвенных измерениях? 9. Как определяется абсолютная погрешность при косвенных измерениях? 10. Что такое доверительный интервал?
Порядок выполнения работы
1. Включить установку в сеть. 2. На маховичок наложить произвольно выбранное кольцо, прижимая его до упора. 3. На ось маятника намотать нить подвески, обращая внимание на то. чтобы она наматывалась равномерно, виток к витку. 4. Зафиксировать маятник в верхнем кронштейне отжатием клавиши "ПУСК" секундомера. 5. Нажать клавишу "СБРОС" секундомера. 6. Нажать клавишу "ПУСК", при этом электронный секундомер начнет отсчет времени движения маятника до нижнего кронштейна. Измерения повторить 5 раз и занести в соответствующую колонку таблицы. 7. По шкале на вертикальной колонке определить длину 8. Измерения времени (пункт 6) повторить для разных насадных колец и занести в таблицу.
9. Определить общую массу маятника. Значения масс отдельных элементов указаны на них. 10. По формуле (10) вычислить момент инерции 11. Вычислить относительную и абсолютную погрешности определения момента инерции по полученным самостоятельно формулам. 12. Вычислить теоретические значения моментов инерции маятника но формулам (11) и сравнить с вычисленным по формулам (10):
где
13. Записать окончательный результат с учетом погрешностей. 14. По полученным результатам сделать выводы. 15. Результаты измерений и вычислений занести в табл. 1 и табл. 2.
Т а б л и ц а 1
Т а б л и ц а 2
Контрольные вопросы
1. Дайте определение момента инерции материальной точки и твердого тела. 2. Как записывается основное уравнение динамики вращательного движения? 3. Какой физический прибор называется маятником Максвелла? Назовите основные его элементы и объясните принцип его работы. 4. Выведите рабочую формулу для определения момента инерции маятника Максвелла. 5. Объясните формулу (11) для теоретических значений моментов инерции маятника. 6. Выведите формулу для относительной и абсолютной погрешностей определения моментов инерции. Лабораторная работа 2.2 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА Цель работы: Изучить законы динамики вращательного движения твердого тела с помощью махового колеса. Определить момент инерции махового колеса.Экспериментально исследовать величину момента инерции махового колеса в зависимости от условий эксперимента. Приборы и принадлежности: маховое колесо, грузы, линейка, штангенциркуль, секундомер.
Порядок выполнения работы
1. Установить положение нижней части груза m на нулевую отметку. 2. Поднять груз, наматывая шнур на шкив, на высоту 3. Отпустить груз, одновременно включая секундомер. Измерить время опускания груза 4. Измерить высоту подъема груза m после опускания его на нулевую отметку. 5. Повторить измерения 6. Изменить массу груза m, отделив его нижнюю часть. Не изменяя высоты 7. Результаты измерений занести в табл. 1: Т а б л и ц а 1
8. По указанию преподавателя изменить высоту подъема груза 9. Результаты измерений занести в табл. 2.
Т а б л и ц а 2
10. Вычислить моменты инерции I махового колеса по формуле (4) для заданных условий эксперимента. Найти среднее арифметическое значение I. 11. По формуле (3) вычислить силу трения в 12. Оценить погрешности eI, DI, 13. По результатом работы сделать выводы о величинах I и fтр.
Контрольные вопросы 1. Какой закон положен в основу вывода расчетной формулы для момента инерции? 2. Как определить линейное ускорение груза и угловое ускорение колеса? 3. От чего зависит момент инерции махового колеса? 4. В чем заключается основной закон динамики вращательного движения? 5. Выведите формулу (4). Лабораторная работа 2.3
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ НЕПРАВИЛЬНОЙ ФОРМЫ ДИНАМИЧЕСКИМ МЕТОДОМ
Цель работы: определение момента инерции тела неправильной формы с помощью законов динамики вращательного движения. Приборы и принадлежности: установка для определения момента инерции тела неправильной формы, штангенциркуль, секундомер.
Порядок выполнения работы
1. Тело А с неизвестным моментом инерции I устанавливается на диск В. 2. К шнуру подвешивается груз 3. Отпуская груз, одновременно включить секундомер, измерить время падения груза t1. 4. Повторить измерения 5 раз. 5. Изменить массу груза 6. Провести аналогичные измерения с грузом 7. Снять исследуемое тело А с диска В. 8. Провести измерения времени падения
9. Провести измерения времени падения 10. Штангенциркулем измерить диаметр вала, на который наматывается шнур, вычислить радиус вала 11. Занести измерения в табл. 1.
Т а б л и ц а 1
12. По формуле (7) вычислить момент инерции тела I, подставляя средние значения t1ср, t2ср, 13. Сделать вывод по результатам исследований. 14. Оценить абсолютные погрешности прямых измерений величин и занести в табл. 2.
Т а б л и ц а 2
Контрольные вопросы
1. В чем заключается динамический метод определения момента инерции тел неправильной формы? 2. Что характеризует момент инерции тела? 3. В чем заключается теорема Штейнера? 4. Как определить кинетическую энергию вращающегося тела? 5. Выведите рабочую формулу (7) Лабораторная работа 2.4 МАЯТНИК ОБЕРБЕКА Цель работы: экспериментально исследовать зависимость момента инерции маятника Обербека от положения грузов Приборы и принадлежности: маятник Обербека, линейка, штангенциркуль, секундомер.
Порядок выполнения работы
I. Установить положение верхней части груза 2.Установить положение каждого груза 3. Поднять груз 4. Измерить время 5. Повторить измерения времени падения груза, не изменяя заданную высоту поднятия груза 6. Повторить пункты 2-5 для разных расстояний 7. Штангенциркулем измерить диаметр шкива, на который наматывается шнур, рассчитать радиус шкива 8. Результаты измерений занести в таблицы 1 и 2. Таблица 1
Т а б л и ц а 2
9. По средним значениям времени t для каждого из пяти положений грузов вычислить момент инерции по формуле (4). 10. Вывести формулы и определить относительную и абсолютную погрешности для момента инерции.
11. Построить на миллиметровой бумаге график зависимости момента инерции маятника Обербека от квадрата расстояния грузов на стержнях от оси вращения 12. Проанализировать полученные результаты.
Контрольные вопросы
1. На основании какого закона выводится рабочая формула? 2. Как зависит момент инерции маятника Обербека от расположения грузов на стержнях? 3. Что характеризует момент инерции тела? 4. Какая связь между линейным и угловым ускорением?
СОУДАРЕНИЕ ТЕЛ Абсолютно упругий удар
При абсолютно упругом ударе наблюдается превращение кинетической энергии в потенциальную и обратно. Абсолютно упругий удар – это столкновение тел, в результате которого их внутренние энергии не меняются. При центральном ударе абсолютно упругих шаров кинетическая энергия шаров, связанная с движением их центра масс, измениться не может, так как не может измениться скорость самого центра масс. Претерпевает превращение только кинетическая энергия относительного движения шаров В случае абсолютно упругого удара шары при столкновении сплющиваются, и кинетическая энергия частично переходит в потенциальную энергию упругих деформаций. В некоторый момент вся кинетическая энергия относительного движения переходит в потенциальную энергию упруго деформированных шаров. В этот момент шары стремятся перейти в недеформированное состояние. Начинается обратный процесс перехода энергии упругих деформаций в кинетическую энергию поступательного движения шаров. Когда он заканчивается, шары разлетаются в разные стороны и вновь оказываются не деформированными. При абсолютно упругом соударении выполняются важные законы сохранения: закон сохранения импульса и закон сохранения кинетической энергии:
где v1 и v2 – скорости тел до удара,
Так как
т.е.
Допустим, что второй шар в начале был неподвижным
Абсолютно неупругий удар Примером, где имеет место потеря механической энергии под действием диссипативных сил, является абсолютно неупругий удар. Так называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело. Рассмотрим физические явления при столкновении тел.
Пусть шары движутся вдоль прямой, соединяющей их центры, со скоростями
откуда:
Кинетические энергии системы до удара и после удара равны:
При неупругом соударении тел кинетическая энергия не сохраняется. Энергия, равная
переходит во внутреннюю энергию тел. Решая совместно уравнения (1) и (2), получим:
где Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кинетической энергии макроскопического движения, равная половине произведения приведенной массы на квадрат их относительной скорости. Лабораторная работа 3.1 Порядок выполнения работы
1.Зафиксировать электромагнит соответственно заданному преподавателем углу отклонения правого шара 2. Включить сеть ~ 220 В (ключ К1). 3. Включить электромагнит (ключ К2). 4. Подвести правый шар к электромагниту и установить магнит для левого шара на необходимый угол. 5. Зарядить блок питания (ключ К3). 6. Левый шар установить отвесно. 7. Нажать кнопку сброса показаний вольтметра (К4). 8. Выключить электромагнит (ключ К2). 9. Произвести измерение напряжения на вольтметре. 10.Повторить измерения 5 раз, не изменяя угла опускания шара. 11. Занести значения заданных величин в табл. 1. 12. Занести значения экспериментально измеренных величин в табл. 2.
Т а б л и ц а 1
Т а б л и ц а 2
13. По средним значениям U вычислить для каждого из трех углов значения времени удара, силы удара, скорости левого шара после удара по формулам (I), (2), (4), а также их относительные и абсолютные погрешности по формулам, полученным самостоятельно. 14. Записать окончательный результат, проанализировать полученные результаты.
Контрольные вопросы
1. Чем отличается абсолютно упругий удар от абсолютно неупругого удара? 2. Какой метод использован в данной работе для определения малых промежутков времени? 3. В чем заключается закон сохранения импульса и механической энергии?
4. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Основные теоретические положения Колебания – это процессы, характеризующиеся определённой повторяемостью во времени. Простейшим примером колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса. Гармонические колебания обобщенной величины S описываются уравнением типа:
где А – амплитуда колебания – максимальное значение колеблющейся величины ω0 – циклическая (круговая) частота; φ =ω0 t+φ0 – фаза колебания; φ0 – начальная фаза – фаза колебаний в момент времени t=0.
Линейная частота – число колебаний за 1 секунду, т. е.
где Т. к. циклическая частота
Запишем первую и вторую производную от величины S:
Из последнего выражения следует, что
Это уравнение является дифференциальным уравнением свободных незатухающих гармонических колебаний. Колебания называются свободными, если они совершаются за счёт первоначально сообщенной энергии. Решением полученного дифференциального уравнения (2) является выражение (1). Колеблющиеся системы, описываемые уравнениями вида
называются гармоническими осцилляторами. В качестве примера гармонического осциллятора рассмотрим колебания физического маятника. Физический маятник – это любое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести (т. О – точка подвеса тела (см. рис. 4.1)). Если маятник отклонен от положения равновесия на некоторый угол α (рис. 4.1), то согласно уравнению динамики вращательного движения
где М – момент силы, создаваемый вращающей силой
Уравнение динамики будет иметь вид:
где І – момент инерции маятника относительно оси, проходящей через точку О; l – расстояние между точкой подвеса и центром масс маятника. Знак минус обусловлен тем, что направление движения и сила Т. к.
Или
Принимая
получим
Это уравнение идентично уравнению (2), решение которого известно. В переменных a оно будет иметь вид:
Из этого уравнения следует, что при малых колебаниях физический маятник совершает гармонические колебания с периодом:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 845; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.142.146 (0.189 с.) |
 Общий вид экспериментальной установки представлен на рис. 1.1.
Общий вид экспериментальной установки представлен на рис. 1.1.  ,
, - его длина;
- его длина;  - площадь поперечного сечения;
- площадь поперечного сечения;  - удельное сопротивление (это сопротивление проводника из данного материала длиной 1 м и поперечным сечением 1 мм2). И так как площадь сечения проводника
- удельное сопротивление (это сопротивление проводника из данного материала длиной 1 м и поперечным сечением 1 мм2). И так как площадь сечения проводника  , то
, то  .
.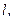 м
м
 м
м
 м
м
 А
А
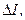 А
А
 В
В
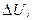 В
В
 Ом·м
Ом·м
 Ом·м
Ом·м
 в данной работе?
в данной работе?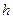 маятника.
маятника. маятника для всех серий измерений.
маятника для всех серий измерений. , (11)
, (11)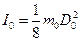 – момент инерции оси маятника,
– момент инерции оси маятника,  – масса оси маятника,
– масса оси маятника,  = 10 мм – диаметр оси маятника;
= 10 мм – диаметр оси маятника; – момент инерции диска,
– момент инерции диска,  – масса диска,
– масса диска,  86 мм – внешний диаметр диска;
86 мм – внешний диаметр диска; – момент инерции насадного кольца,
– момент инерции насадного кольца,  – масса кольца,
– масса кольца,  105 мм – внешний диаметр кольца.
105 мм – внешний диаметр кольца.
 с
с
 с
с
 с
с
 кг
кг
 кг
кг
 кг
кг
 м
м
 м
м
 , м
, м
 , заданную преподавателем.
, заданную преподавателем. , выключив секундомер при достижении нижней части груза нулевой отметки.
, выключив секундомер при достижении нижней части груза нулевой отметки. 5 раз, не изменяя высоту
5 раз, не изменяя высоту 



 опоре махового колеса
опоре махового колеса ,
,  ,
, , шнур накручивается на вал С так, чтобы груз поднялся на высоту
, шнур накручивается на вал С так, чтобы груз поднялся на высоту  на
на  , выкрутив нижнюю часть груза
, выкрутив нижнюю часть груза  груза
груза  с грузом
с грузом  , повторив опыт 5 раз.
, повторив опыт 5 раз. .
.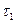

 грузов
грузов  , м/с2
, м/с2





 , указывая на графике абсолютную погрешность
, указывая на графике абсолютную погрешность  .
. .
.
 и
и 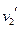 – после удара.Решая эти два уравнения, можно найти скорости тел после соударения
– после удара.Решая эти два уравнения, можно найти скорости тел после соударения 
 и
и  не равны нулю, то уравнения можно поделить почленно. Получим:
не равны нулю, то уравнения можно поделить почленно. Получим: ,
, ,
,  .
. , а под действием удара он начал двигаться
, а под действием удара он начал двигаться  , тогда
, тогда  . Таким образом, при равенстве масс двух соударяющихся шаров, один из которых неподвижен, движущийся шар полностью передает импульс неподвижному и останавливается. Поэтому
. Таким образом, при равенстве масс двух соударяющихся шаров, один из которых неподвижен, движущийся шар полностью передает импульс неподвижному и останавливается. Поэтому  . Если второй шар остается в покое, то D v=v2 –
. Если второй шар остается в покое, то D v=v2 –  .
. Сталкивающиеся тела деформируются, возникают упругие силы и сила трения, в телах возбуждаются колебания и упругие волны. Но если удар неупругий, то в конце концов все эти процессы прекращаются, и оба тела, соединившись вместе, движутся как единое тело. Его скорость можно найти, используя закон сохранения импульса.
Сталкивающиеся тела деформируются, возникают упругие силы и сила трения, в телах возбуждаются колебания и упругие волны. Но если удар неупругий, то в конце концов все эти процессы прекращаются, и оба тела, соединившись вместе, движутся как единое тело. Его скорость можно найти, используя закон сохранения импульса. и
и  , v – общая скорость шаров после столкновения. По закону сохранения импульса:
, v – общая скорость шаров после столкновения. По закону сохранения импульса: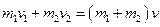 ,
, . (1)
. (1) ;
;  .
. , (2)
, (2) ,
, – приведенная масса шаров,
– приведенная масса шаров, 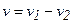 – относительная скорость движения шаров.
– относительная скорость движения шаров. .
. %
%
 %
%
 рад
рад

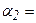

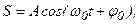 (1)
(1)
 – период колебаний – время, в течение которого совершается одно полное колебание.
– период колебаний – время, в течение которого совершается одно полное колебание. линейная частота будет равна
линейная частота будет равна 


 (2)
(2)
 ,
, , которая является составляющей силы тяжести Р и равна:
, которая является составляющей силы тяжести Р и равна: .
. Для малых углов
Для малых углов  , тогда
, тогда  , и момент возвращающей силы
, и момент возвращающей силы  .
. ,
, имеют разное направление.
имеют разное направление. , то уравнение динамики можно записать в виде:
, то уравнение динамики можно записать в виде: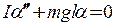 .
. .
. ,
, .
.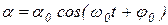 .
.


