
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о пределе сжатой переменной ⇐ ПредыдущаяСтр 6 из 6
Теорема. Пусть даны три последовательности Доказательство. 1. Возьмем любое 2. По этому числу 3. По этому жечислу
4. Обозначим через N наибольший номер из N1 и N2: 5. Тогда при
6. Подчеркнем левую часть первого неравенства и правую часть второго неравенства. 7. Используя подчеркнутые неравенства, а также неравенства, данные в условии теоремы, получаем Ч.т.д. 14.Теорема о необходимом и достаточном условии сходимости последовательности к числу а Огюстен Луи Коши – французский математик (1798 - 17857). До сих пор не было дано достаточно общего критерия, с помощью кото-рого можно было бы узнать, сходится или нет данная последовательность. Само определение предела последовательности содержит значение пре-дела, которое может быть неизвестным. Необходимо иметь такой критерий для определения сходимости и рас-ходимости последовательности, который базировался бы только на свойствах элементов данной последовательности. Теорема о необходимом и достаточном условии сходимости последова-тельности дает как раз подобный критерий. Определение. Последовательность
Определение. Последовательность, удовлетворяющая условию Коши, называется фундаментальной последовательностью [29]. Теорема (Критерий Коши). Для того, чтобы последовательность схо-дилась необходимо и достаточно, чтобы она удовлетворяла условию Коши. Доказательство необходимости. 1. Пусть последовательность 2. Зададим произвольное 3. Тогда согласно определению предела последовательности существует такой номер элемента
4. Возьмем еще один номер элемента
5. Сложим два неравенства п.3. и п.4.: 6. Воспользуемся свойством модуля разности двух действительных чисел ( Ч.т.д.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.9.141 (0.005 с.) |
 ,
,  и
и  , при-чем
, при-чем 
 . Пусть последовательности
. Пусть последовательности  и
и  имеют один и тот же предел а:
имеют один и тот же предел а:  . Тогда последовательность
. Тогда последовательность  так-же имеет предел а:
так-же имеет предел а:  .
. .
. для последовательности
для последовательности  найдется такой номер
найдется такой номер  , что
, что 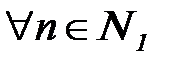 :
: 

 . (3)
. (3) найдется номер
найдется номер 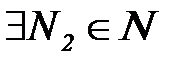 , что n>N2 будет выполняться неравенство:
, что n>N2 будет выполняться неравенство: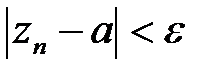
 . (4)
. (4) .
. n>N будут выполняться одновременно два неравенства
n>N будут выполняться одновременно два неравенства и
и  .
. при n>N. Отсюда
при n>N. Отсюда  или
или  при n>N. Это означает, что
при n>N. Это означает, что  , что для всех номеров
, что для всех номеров  удовлетворяющих неравенству
удовлетворяющих неравенству  и
и  , справедливо неравенство:
, справедливо неравенство: . (5)
. (5) . Требуется доказать, что эта последовательность удовлетворяет условию Коши.
. Требуется доказать, что эта последовательность удовлетворяет условию Коши. (
( ).
). , что
, что 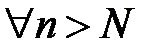 выполняется неравенство
выполняется неравенство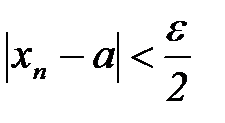 .
. , тогда должно выполняться неравенство
, тогда должно выполняться неравенство  .
. .
. ):
):  или
или 


