
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Промежутки действительных чисел
I. Ограниченный промежутки: а) отрезки
б) интервалы
в) полуинтервалы: 1.
2.
Замечание. В случае Определение 1. Интервал II. Неограниченные промежутки. а) интервалы:
б) полуинтервалы:
Определение 2. Отрезки, интервалы, полуинтервалы называются промежутками, а точки а, Определение 3. Если а и b – конечные числа, то действительное число Определение 4. Если хоть одно из чисел а и b является бесконечным, то промежуток называется бесконечным. Свойство промежутков всех типов расширенной числовой прямой. Если точки Примеры: 1. Из отрезка Ответ: Остались концы промежутка: точка Или через множество: 2. Из отрезка Ответ: 3. Из интервала Ответ: Понятие Определение. Если Обозначается На координатной прямой:
1. Если
2. Если
Замечание 1. При определении Замечание 2. В общем случае Пример. Дано неравенство Множество действительных чисел
Модуль Тема №1 Действительные числа и их свойства
Лекция №3 1. Лемма о непересекающихся окрестностях. 2. Ограниченные и неограниченные множества. 3. Верхняя и нижняя грани числовых множеств. 4. Свойства точных граней множества. 5. Плотность множества рациональных чисел во множестве действительных чисел.
Лемма Лемма – греческое слово (вспомогательное утверждение, необходимое в цепи логических рассуждений для доказательства некоторой теоремы). Лемма. Пусть Доказательство: I. 1. Если 2. Получим такие окрестности точек
3. Очевидно, что окрестности не пересекаются. II. 1. Если 2. Получим такие окрестности точек
3. Очевидно, что окрестности не пересекаются. III. 1. Если 2. Получим такие окрестности точек
3. Очевидно, что окрестности не пересекаются. IV. 1. Если 2. Покажем это:
ч.т.д. Замечание. Если
Примеры. Определить, какие множества заданы следующими неравенствами. 1.
Ответ: отрезок 2.
Ответ: объединение двух полуинтервалов 3.
Ответ: интервал 4.
Ответ: объединение двух интервалов
|
|||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 828; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.193.45 (0.024 с.) |
 ℝ:
ℝ:  ,
, 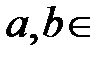 ℝ.
ℝ.
 ℝ:
ℝ:  ,
,  ℝ.
ℝ.
 ℝ:
ℝ:  ,
, 
 ℝ:
ℝ:  ,
, 
 отрезок состоит из одной точки.
отрезок состоит из одной точки. называется внутренностью отрезка
называется внутренностью отрезка  .
. ℝ:
ℝ: 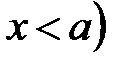 ,
,  ℝ.
ℝ.
 ℝ:
ℝ:  ,
, 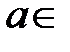 ℝ.
ℝ.
 ℝ.
ℝ. ℝ:
ℝ:  ,
, 
 ℝ:
ℝ: 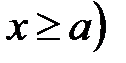 ,
, 
 – их концами, а
– их концами, а  ℝ, b
ℝ, b  ℝ.
ℝ. называется длиной промежутка с концами а и b.
называется длиной промежутка с концами а и b.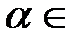 ℝ,
ℝ,  ℝ, причем
ℝ, причем  , принадлежат некоторому промежутку с концами
, принадлежат некоторому промежутку с концами  ℝ,
ℝ, 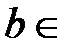 ℝ, то весь отрезок
ℝ, то весь отрезок  принадлежит этому промежутку.
принадлежит этому промежутку. удален интервал
удален интервал  . Что осталось?
. Что осталось? с координатой
с координатой 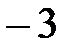 :
:  и точка
и точка  с координатой
с координатой 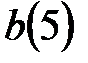 .
. .
. вырезан интервал
вырезан интервал  . Как записать множество оставшихся точек отрезка с помощью промежутков?
. Как записать множество оставшихся точек отрезка с помощью промежутков? – отрезки.
– отрезки. вырезаны два отрезка
вырезаны два отрезка 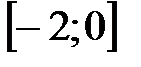 и
и  . Какие промежутки остались?
. Какие промежутки остались? – остались такие интервалы.
– остались такие интервалы. – окрестности
– окрестности является действительным числом, то для любого
является действительным числом, то для любого 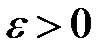
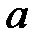 называется интервал
называется интервал 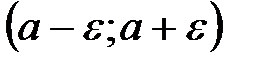 .
.
 .
.
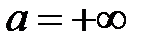 , то
, то  – окрестность точки
– окрестность точки  будет такой U
будет такой U 
 . Графически:
. Графически: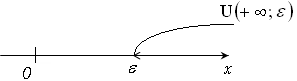
 , то
, то 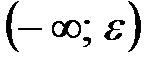
 . Графически:
. Графически: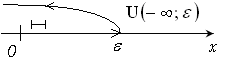
 можно брать не только положительные
можно брать не только положительные  , но и любые
, но и любые  ℝ. Условие
ℝ. Условие  накладывается лишь с целью единообразия определений.
накладывается лишь с целью единообразия определений. может быть записано неравенством
может быть записано неравенством  или
или  , где
, где 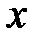 – множество действительных чисел.
– множество действительных чисел. . О чем говорит это неравенство?
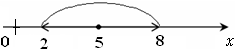
. О чем говорит это неравенство? , удовлетворяющих неравенству
, удовлетворяющих неравенству  ,
,  .
.

 ℝ, причем
ℝ, причем  . Тогда существуют
. Тогда существуют  ,
,  такие, что
такие, что  окрестность точки
окрестность точки 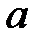 при пересечении с
при пересечении с  окрестностью точки
окрестностью точки  дает пустое множество: U
дает пустое множество: U  U
U  .
. при
при  и
и  :
:
 ℝ, а
ℝ, а  , то в качестве
, то в качестве  подходят:
подходят:  ,
,  .
.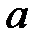 и
и  :
:
 ,
,  ℝ, то в качестве
ℝ, то в качестве  ,
,  .
.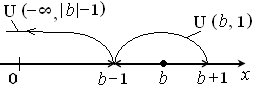
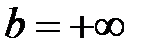 , то при произвольном
, то при произвольном  окрестности точки
окрестности точки  ,
,  не пересекаются.
не пересекаются.
 ℝ и
ℝ и  , то для двух любых
, то для двух любых 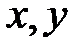 , таких что
, таких что  U
U  ,
,  U
U  справедливо неравенство:
справедливо неравенство:  .
. ℝ,
ℝ, 
 U
U  :
:  или
или  , т. е.
, т. е.  ;
;  .
.
 .
.

 .
.
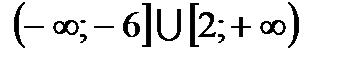 .
. .
.
 .
.

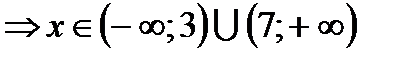

 .
.


