
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы и простейшие действия над ними ⇐ ПредыдущаяСтр 3 из 3
Свободный вектор а (т. е. такой вектор, который без изменения длины и на- правления может быть перенесен в любую точку пространства), заданный в координатном пространстве Oxyz, может быть представлен в виде:
СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ 1. Скалярное произведение. Скалярным произведением двух векторов а и b называется число, равное произведению длин этих векторов на косинус угла ϕ между ними:
3. Смешанное произведение. Смешанным произведением векторов a, b и с называется скалярное произведение вектора aXb на вектор с, т. е. (aXb).c. Смешанное произведение трех векторов а, Ь, с по модулю равно объему па- раллелепипеда, построенного на этих векторах.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ на плоскости ПРЯМАЯ 1. Общее уравнение прямой. Всякое уравнение первой степени относительно х и у, т. е. уравнение вида: (1) Ах+Ву+С=0 наз. общин уравнением прямой (
КРИВЫЕ ВТОРОГО ПОРЯДКА 1. Окружность. Окружность—это множество точек плоскости, равноудален - равноудаленных от данной точки (центра). Если г — радиус окружности, а точка С (а; Ь) — ее центр, то уравнение окружности имеет вид:
Гипербола. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фо- кусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Если поместить фокусы гиперболы в точках F1 (с; 0) и F2(— с; 0), то получится каноническое уравнение гиперболы
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ПЛОСКОСТЬ И ПРЯМАЯ
плоскости,называемый нормальным вектором.
Поверхность второго порядка Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов Типы поверхностей второго порядка Цилиндрические поверхности Поверхность
Теорема (об уравнении цилиндрической поверхности). Кривая, задаваемая уравнением Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
Конические поверхности []
Коническая поверхность. Основная статья: Коническая поверхность Поверхность Функция Теорема (об уравнении конической поверхности). Если поверхность · Каноническое уравнение конуса второго порядка имеет вид:
Поверхности вращения ] Поверхность Теорема (об уравнении поверхности вращения).
В случае, если
Эллиптический параболоид Уравнение эллиптического параболоида имеет вид
Если Пересечение эллиптического параболоида с плоскостью Пересечение эллиптического параболоида с плоскостью Гиперболический параболоид ]
Гиперболический параболоид. Уравнение гиперболического параболоида имеет вид
Пересечение гиперболического параболоида с плоскостью Пересечение гиперболического параболоида с плоскостью Ввиду геометрической схожести гиперболический параболоид часто называют «седлом». Центральные поверхности Если центр поверхности второго порядка существует и единственен, то его координаты
Матричный вид уравнения поверхности второго порядка Уравнение поверхности второго порядка может быть переписано в матричном виде:
Также можно выделить квадратичную и линейную части друг от друга:
Если обозначить
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.183 (0.026 с.) |







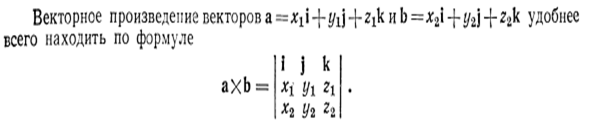


 +
+  ≠0),A,B,C-ПОСТОЯННЫЕ КОЭФИЦИЕНТЫ.
≠0),A,B,C-ПОСТОЯННЫЕ КОЭФИЦИЕНТЫ.














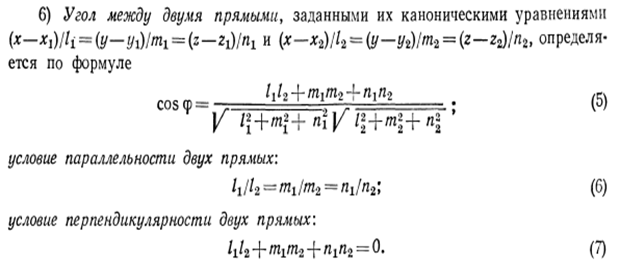



 ,
,  ,
,  ,
, 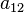 ,
,  ,
,  отличен от нуля.
отличен от нуля. называется цилиндрической поверхностью с образующей
называется цилиндрической поверхностью с образующей  , если для любой точки
, если для любой точки  этой поверхности прямая, проходящая через эту точку параллельно образующей
этой поверхности прямая, проходящая через эту точку параллельно образующей  , то
, то  .
. , называется направляющей цилиндрической поверхности.
, называется направляющей цилиндрической поверхности.
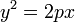








 , если для любой точки
, если для любой точки  называется однородной порядка
называется однородной порядка  , если
, если  выполняется следующее:
выполняется следующее: 
 , где
, где 
 этой поверхности окружность, проходящая через эту точку в плоскости
этой поверхности окружность, проходящая через эту точку в плоскости  с центром в
с центром в  и радиусом
и радиусом  , целиком принадлежит этой поверхности.
, целиком принадлежит этой поверхности. , то
, то 







 , перечисленные выше поверхности являются поверхностями вращения.
, перечисленные выше поверхности являются поверхностями вращения.
 , то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой
, то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой  , вокруг вертикальной оси, проходящей через вершину и фокус данной параболы.
, вокруг вертикальной оси, проходящей через вершину и фокус данной параболы. является эллипсом.
является эллипсом. или
или  является параболой.
является параболой.

 можно найти, решив систему уравнений:
можно найти, решив систему уравнений:


 , то уравнение приобретает следующий вид:
, то уравнение приобретает следующий вид: .
.


