
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители третьего порядка и системы линейных уравнений.Стр 1 из 3Следующая ⇒
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц. Матрицы (и соответственно математический раздел - матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин "матрица" появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков. Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.
Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ. Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,..., ann. Равенство матриц. A=B, если порядки матриц A и B одинаковы и aij=bij(i=1,2,...,m; j=1,2,...,n) Действия над матрицами.
1. Сложение матриц - поэлементная операция
. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B. Покажем операцию умножения матриц на примере:
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами Пример
Свойства опeраций над матрицами A+B=B+A (A+B)+C=A+(B+C) λ(A+B)=λA+λB A(B+C)=AB+AC (A+B)C=AC+BC λ(AB)=(λA)B=A(λB) A(BC)=(AB)C Виды матриц 1. Прямоугольные: m и n - произвольные положительные целые числа 2. Квадратные: m=n 3. Матрица строка: m=1. Например, (1 3 5 7) - во многих практических задачах такая матрица называется вектором 4. Матрица столбец: n=1. Например
5. Диагональная матрица: m=n и aij=0, если i≠j. Например
6. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,...,m j=1,2,...,n
8. Треугольная матрица: все элементы ниже главной диагонали равны 0. Пример.
9. Квадратная матрица: m=n и aij=aji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=A Например,
Пример
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам. Примеры решения систем линейных алгебраических уравнений матричным методом. Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц. Пример. С помощью обратной матрицы найдите решение системы линейных уравнений
Решение. В матричной форме исходная система запишется как, Обратную матрицу
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Полярные координаты. В полярной системе координат положение точки М
ρ
0 х
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ В ПРОСТРАНСТВЕ
ПРЯМАЯ 1. Общее уравнение прямой. Всякое уравнение первой степени относительно х и у, т. е. уравнение вида: (1) Ах+Ву+С=0 наз. общин уравнением прямой (
КРИВЫЕ ВТОРОГО ПОРЯДКА 1. Окружность. Окружность—это множество точек плоскости, равноудален - равноудаленных от данной точки (центра). Если г — радиус окружности, а точка С (а; Ь) — ее центр, то уравнение окружности имеет вид:
Гипербола. Гиперболой называется множество точек плоскости, абсолютная
величина разности расстояний которых до двух данных точек, называемых фо- кусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Если поместить фокусы гиперболы в точках F1 (с; 0) и F2(— с; 0), то получится каноническое уравнение гиперболы
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ПЛОСКОСТЬ И ПРЯМАЯ
плоскости,называемый нормальным вектором.
Поверхность второго порядка Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов Типы поверхностей второго порядка Цилиндрические поверхности Поверхность Теорема (об уравнении цилиндрической поверхности). Кривая, задаваемая уравнением Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
Конические поверхности []
Коническая поверхность. Основная статья: Коническая поверхность Поверхность Функция Теорема (об уравнении конической поверхности). Если поверхность · Каноническое уравнение конуса второго порядка имеет вид:
Поверхности вращения ] Поверхность Теорема (об уравнении поверхности вращения).
В случае, если Эллиптический параболоид Уравнение эллиптического параболоида имеет вид
Если
Пересечение эллиптического параболоида с плоскостью Пересечение эллиптического параболоида с плоскостью Гиперболический параболоид ]
Гиперболический параболоид. Уравнение гиперболического параболоида имеет вид
Пересечение гиперболического параболоида с плоскостью Пересечение гиперболического параболоида с плоскостью Ввиду геометрической схожести гиперболический параболоид часто называют «седлом». Центральные поверхности Если центр поверхности второго порядка существует и единственен, то его координаты
Матричный вид уравнения поверхности второго порядка Уравнение поверхности второго порядка может быть переписано в матричном виде:
Также можно выделить квадратичную и линейную части друг от друга:
Если обозначить
ПРЕДЕЛЫ
----------------------------------------------------------------------------------------
СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Определители третьего порядка и системы линейных уравнений. ОпределиТЕЛЬ третьего порядка, соответствующий таблице элементов
Минором данного элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент. Алгебраическим дополнением данного элемента называется его минор, умноженный на Таким образом, знак, который при этом приписывается минору соответствующего элемента определителя, пределяется следующей таблицей:
В приведенном выше равенстве, выражающем определитель третьего порядка, в правой части стоит сумма произведений элементов 1-й строки определителя на их алгебраические дополнения. Теорема 1. Определитель третьего порядка равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения. Эта теорема позволяет вычислять значение определителя, раскрывая его по элементам любой его строки или столбца.
Теорема 2. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю. Свойства определителей. 1°. Определитель не изменится, если строки определителя заменить столб- цами, а столбцы—соответствующими строками. 2°. Общий множитель элементов какой-нибудь строки (или столбца) может быть вынесен за знак определителя. 3°. Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца), то определитель равен нулю. 4°. При перестановке двух строк (столбцов) определитель меняет знак на противоположный. 5°. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число (теорема о линейной комбинации параллельных рядов определителя). Решение системы трех линейных уравнений с тремя неизвестными.
находится по формулам Крамера
где
При этом предполагается, что D ≠0 (если D = 0, то исходная система либо неопределенная, либо несовместная).
Если,система однородная, т. е. имеет вид и ее определитель отличен от нуля, то она имеет единственное решение х= 0, у=о, z = o. Если же определитель однородной системы равен нулю, то система сводится либо к двум независимым уравнениям (третье является их следствием), либо к одному уравнению (остальные два являются его следствиями). Первый случай имеет место тогда, когда среди миноров определителя однородной системы есть хотя бы один отличный от нуля, второй—тогда, когда все миноры этого опреде лителя равны нулю. В обоих случаях однородная система имеет бесчисленное множество решений. Вычислить определитель третьего порядка
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.221.204 (0.084 с.) |















 .
. где
где  . Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем
. Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем  , следовательно, для матрицы А может быть найдена обратная матрица
, следовательно, для матрицы А может быть найдена обратная матрица 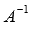 . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как
. Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как  . Итак, задача свелась к построению обратной матрицы
. Итак, задача свелась к построению обратной матрицы  можно найти по следующей формуле:
можно найти по следующей формуле: , где
, где  – определитель матрицы А,
– определитель матрицы А,  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.


 Y
Y М
М θ
θ

 +
+  ≠0),A,B,C-ПОСТОЯННЫЕ КОЭФИЦИЕНТЫ.
≠0),A,B,C-ПОСТОЯННЫЕ КОЭФИЦИЕНТЫ.














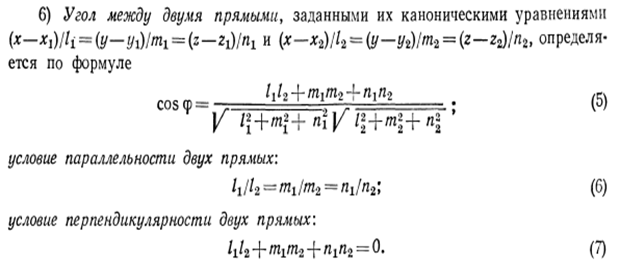



 ,
,  ,
,  ,
, 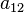 ,
,  ,
,  отличен от нуля.
отличен от нуля. называется цилиндрической поверхностью с образующей
называется цилиндрической поверхностью с образующей  , если для любой точки
, если для любой точки  этой поверхности прямая, проходящая через эту точку параллельно образующей
этой поверхности прямая, проходящая через эту точку параллельно образующей  , то
, то  .
. , называется направляющей цилиндрической поверхности.
, называется направляющей цилиндрической поверхности.
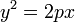








 , если для любой точки
, если для любой точки  называется однородной порядка
называется однородной порядка  , если
, если  выполняется следующее:
выполняется следующее: 
 , где
, где 
 этой поверхности окружность, проходящая через эту точку в плоскости
этой поверхности окружность, проходящая через эту точку в плоскости  с центром в
с центром в  и радиусом
и радиусом  , целиком принадлежит этой поверхности.
, целиком принадлежит этой поверхности. , то
, то 







 , перечисленные выше поверхности являются поверхностями вращения.
, перечисленные выше поверхности являются поверхностями вращения.
 , то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой
, то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой  , вокруг вертикальной оси, проходящей через вершину и фокус данной параболы.
, вокруг вертикальной оси, проходящей через вершину и фокус данной параболы. является эллипсом.
является эллипсом. или
или  является параболой.
является параболой.

 можно найти, решив систему уравнений:
можно найти, решив систему уравнений:


 , то уравнение приобретает следующий вид:
, то уравнение приобретает следующий вид: .
.








 определяется равенством
определяется равенством
 , где k сумма номеров строки и столбца, содержащих данный элемент.
, где k сумма номеров строки и столбца, содержащих данный элемент.









