
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная и дифференциал функции.
Исследование функций и построение графиков Цель занятия: Научиться находить производные основных элементарных функций, уметь исследовать функции с помощью производной.
Вопросы 1. Понятие производной. 2. Правила дифференцирования. Формулы дифференцирования. 3. Дифференциал функции. 4. Возрастание и убывание функции. 5. Экстремумы функции. Условия экстремума функции. 6. Выпуклость и вогнутость графика функции. Точки перегиба. 7. Построение графиков функций.
Решение типовых задач 1. Найти производные следующих функций: а) Решение. Вычислим производные данных функций: а)
б)
в) 2. Найти производные функций: а) Решение. а) б) 3. Найти производную 2-ого порядка от функции Решение. 4. Найти дифференциалы функции: а) Решение. а) Вычислим производную функции:
Дифференциал функции найдем по формуле
б) Вычислим дифференциал по аналогии с предыдущим примером:
5. Исследовать функцию Решение. 1. Область определения функции: 2. Функция не является ни четной, ни нечетной. 3. Точки пересечения с осями координат. Пусть График пересекает ось Ох в точках 4. Найдем интервалы возрастания и убывания и экстремумы функции. Найдем
Выясним знак
При переходе через точку
Функция убывает на интервале на 5. Найдем интервалы выпуклости и вогнутости функции и точки перегиба. Найдем производную второго порядка
Исследуем знак
В интервале Итак, при переходе через точки
6.
Задания для самостоятельного решения 1. Найдите производные и дифференциалы указанных функций: 1. 3. 5.
2. Найдите значение производной функции
3. Найдите производные второго порядка функций:
а) 4. Определите точки экстремума функций: 1) 5. Исследуйте функцию и постройте ее график
ЗАНЯТИЕ 5 (4 часа) Неопределенный интеграл Цель занятия: Освоить основные методы интегрирования.
Вопросы 1. Неопределенный интеграл, его основные свойства. Таблица основных интегралов. 2. Методы интегрирования (непосредственное интегрирование, метод подстановки, интегрирование по частям). Решение типовых задач Найти неопределенные интегралы: а) Решение. Воспользуемся методом непосредственного интегрирования:
б) Решение. Применим подстановку
в) Решение. Воспользуемся методом интегрирования по частям. Для этого полагаем
Примеры для самостоятельного решения 4) Найти неопределенные интегралы: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
ЗАНЯТИЕ 6 (4 часа)
|
|||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.149.242 (0.013 с.) |
 ; б)
; б)  ; в)
; в)  .
. .
.

 .
.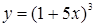 ; б)
; б)  .
. .
. .
. .
.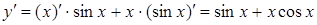 . Дифференцируя производную
. Дифференцируя производную  , получаем:
, получаем:  .
. ; б)
; б)  .
. .
.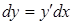 :
: .
.
 .
. и построить ее график.
и построить ее график. .
. , тогда
, тогда  ;
; и
и  .
.
 при
при  и
и  .
.



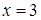 производная
производная  .
. и возрастает на интервале
и возрастает на интервале  .
. ;
;
 ,
,  .
. в окрестности точек
в окрестности точек 
 .
.
 кривая вогнута, в интервале
кривая вогнута, в интервале  кривая выпуклая, в интервале
кривая выпуклая, в интервале  кривая вогнута.
кривая вогнута. ;
; 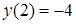 .
. Построим график функции
Построим график функции ;
;  ;
; ; 4.
; 4.  ;
; ; 6.
; 6.  .
. в заданной точке
в заданной точке  :
: ,
,  .
. ; б)
; б)  .
. ; 2)
; 2)  .
. .
. .
. .
. .
. , откуда
, откуда  . Дифференцируя, получаем
. Дифференцируя, получаем  , следовательно,
, следовательно,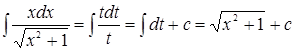 .
. .
. . Согласно формуле интегрирования по частям
. Согласно формуле интегрирования по частям  , получим:
, получим: .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.


