Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические дополнения и миноры.
1º Минором некоторого элемента 2º Алгебраическое дополнение элемента 3º Определитель равен сумме произведений элементов, какого-нибудь столбца (или строки) на их алгебраические дополнения. Например,
Пример 1. Вычислить определитель:
3. Решение системы методом Крамера. Исследование системы.
Решением системы называется совокупность чисел Совместная система называется определенной, если она имеет только одно решение и неопределенной, если она имеет более одного решение. Если
при условии, что определитель системы
не равен нулю, имеет следующее единственное решение:
где
1. Элементы двух строк определителя пропорциональны, например: а) если б) если 2. Если найдутся числа
тогда: а) если б) если
Пример 2. Дана система линейных уравнений:
Установить, что система совместна и найти её решение методом Крамера. Решение. Вычислим определитель системы методом разложения его по элементам строки. Разложим по первой строке:
Так как определитель системы не равен нулю, система уравнений совместна и имеет единственное решение. Найдём решение системы по формуле Крамера.
Пример 3. Решить систему уравнений.
Решение.
Пример 4. Решить систему уравнений:
Решение.
Следовательно, получим Контрольные вопросы 1. Определители. 2. Алгебраические дополнения и миноры. 3. Решение системы методом Крамера. Исследование системы.
Задания. 1. Вычислить определители, разложив их по элементам:а) первого столбца; б) по элементам третьей строки.
2. Найти площадь треугольника с вершинами 3. Вычислить миноры и алгебраические дополнения элементов второй строки определителя.
4. Решить системы уравнений методом Крамера.
. Занятие3 1. Матрицы. Прямоугольная таблица чисел вида
называется матрицей третьего порядка, а определитель
соответствующим определителем этой матрицы. Прямоугольная таблица чисел вида
называется матрицей второго порядка, а определитель
соответствующим определителем этой матрицы.
1.Матрица A называется невырожденной, если 2.Если элементы 3.Две матрицы 4. Нулевой матрицей называется матрица все элементы которого равны нулю 5. Единичной матрицей называется матрица
Элементарными преобразованиями матриц являются: 1) Перестановка местами двух параллельных строк (столбцов) матрицы; 2) Умножение всех элементов строки (столбца) матрицы на число, отличное то нуля; 3)Прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов параллельной строки (столбца), умноженных на одно и то же число. Две матрицы A и
т.е. элемент матрицы – произведения стоящей в Для произведения двух матриц переместительный закон, вообще говоря, не выполняется: Определитель произведения двух матриц равен произведению определителей этих матриц Обратная матрица 1)Матрица B называется обратной по отношению к матрице А, если 2) Всякая невырожденная матрица имеет обратную матрицу. 3) Обратная матрица к матрице
где
4)Обратная матрица к матрице
где Пример1. Найти сумму и произведения матриц
Решение.
Пример 2. Найти обратную матрицу к матрице Решение. Вычисляем определитель матрицы: Находим алгебраические дополнения элементов этого определителя:
Следовательно,
3. Матричный способ решения линейных уравнений. Матрицей – столбцом называется матрица вида Произведение
Система уравнений
может быть записана в виде
где Решение этой системы имеет вид
Пример 3. Решить систему уравнений с помощью обратной матрицы Решение. Перепишем систему в виде где Решение матричного уравнения имеет вид Вычислим алгебраические дополнения элементов этого определителя:
Таким образом, Откуда Следовательно, Пример 4 Решить матричные уравнения
Решение. 1) Найдем обратную матрицу
где
2)Умножим слева правую и левую части равенства 3) Умножим справа правую и левую части равенства 4) Таким образом:
Ранг матрицы. Пусть дана прямоугольная матрица
Выделим в этой матрице k произвольных строк и k произвольных столбцов Рассмотрим всевозможные миноры матрицы A, отличные от нуля. Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг этой матрицы принимают равным нулю. Всякий отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором матрицы. Ранг матрицы А будем обозначать r(A). Ранг матрицы не изменяется от элементарных преобразований. Пример 5. Определить ранг и найти базисные миноры матрицы.
Решение. Имеем Все миноры третьего порядка равны нулю. Базисными минорами является миноры второго порядка этой матрицы отличные от нуля:
Итак, ранг данной матрицы r(A)=2.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.183.14 (0.086 с.) |
 определителя, называется определитель, получаемый из данного определителя путём вычёркивания строки и столбца, на пересечении которых расположен этот элемент и обозначается
определителя, называется определитель, получаемый из данного определителя путём вычёркивания строки и столбца, на пересечении которых расположен этот элемент и обозначается  . Например, минором элемента
. Например, минором элемента  определителя
определителя 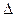 =
=  является определитель
является определитель  =
=  , минором элемента
, минором элемента 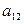 является определитель
является определитель  =
=  и т.д..
и т.д.. .
. .
.
 Пусть дана система линейных уравнений с тремя неизвестными
Пусть дана система линейных уравнений с тремя неизвестными 
 , при подстановке которых все уравнения системы обращаются в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет решения.
, при подстановке которых все уравнения системы обращаются в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет решения. все равны нулю, то система называется однородной.
все равны нулю, то система называется однородной. Система трех линейных уравнений с тремя неизвестными
Система трех линейных уравнений с тремя неизвестными


 (5)
(5) ;
;  ;
;  =
=  .
. Если определитель системы
Если определитель системы  , то возможны два предположения:
, то возможны два предположения: , тогда:
, тогда:
 ,то система не совместна;
,то система не совместна;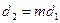 , то система не определена;
, то система не определена; и
и  такие, что:
такие, что: ,
, 

 , то система не совместна;
, то система не совместна; , то система не определена.
, то система не определена.

 ;
;  ;
; 



 ;
;  ;
; 

 и
и  . Однако система не имеет решений. В самом деле, умножим первое уравнение на -2 и сложим со вторым уравнением системы, получим
. Однако система не имеет решений. В самом деле, умножим первое уравнение на -2 и сложим со вторым уравнением системы, получим  , что не возможно, т.е. система не совместна и не имеет решений.
, что не возможно, т.е. система не совместна и не имеет решений.
 Система имеет бесконечно много решений. В самом деле, складывая первые два уравнения, получаем третью и данная система имеет два существенных уравнения:
Система имеет бесконечно много решений. В самом деле, складывая первые два уравнения, получаем третью и данная система имеет два существенных уравнения:

 ,
,  .
. ,
,  ,
, 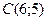 .
. .
. ,
,  ,
,  .
.






 и вырожденной (особой), если
и вырожденной (особой), если  .
. , то матрица называется симметрической
, то матрица называется симметрической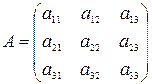 и
и  считается равными
считается равными  тогда и только тогда когда
тогда и только тогда когда 
 .
.
 ,
, 
 Элементарные преобразование матриц.
Элементарные преобразование матриц. B называются эквивалентными, если одна из них получится из другой с помощью элементарных преобразований.
B называются эквивалентными, если одна из них получится из другой с помощью элементарных преобразований. Суммой двух матриц А и В называется матрица А+В, определяемое равенством
Суммой двух матриц А и В называется матрица А+В, определяемое равенством
 называется матрица
называется матрица  , определяемое равенством
, определяемое равенством
 Произведением двух матриц A и B называется матрица AB определяемое равенством
Произведением двух матриц A и B называется матрица AB определяемое равенством ,
, -й строке и k - м столбце, равен сумме произведений соответствующих элементов i-ой строки матрицы A и k -го столбца матрицы B.
-й строке и k - м столбце, равен сумме произведений соответствующих элементов i-ой строки матрицы A и k -го столбца матрицы B. .
. .
. . Матрицу, обратную по отношению к матрице A, принято обозначать
. Матрицу, обратную по отношению к матрице A, принято обозначать  .
. ,
, -алгебраическое дополнение элемента
-алгебраическое дополнение элемента  .
.

 - алгебраические дополнения элемента
- алгебраические дополнения элемента  определителя
определителя  .
. и
и 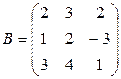 .
. ,
, 


 ;
;  ;
;  :
: ;
;  ;
; 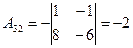 ;
; ;
;  ;
;  .
. .
. .
. определяется равенством:
определяется равенством:

 ,
, .
. , если
, если 
 ,
, ,
,  ,
,  .
.
 ;
;  ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
;  .
. .
.
 ,
,  ,
,  .
. , где
, где 
 .
. . Обратная матрица к матрице
. Обратная матрица к матрице  -ой строки и
-ой строки и  -го столбца.
-го столбца. , то
, то  .
. на
на  .
. на
на  .
. ,
, .
. .
. . Определитель k- го порядка, составленный из элементов матрицы A, расположенных на пересечении выделенных строк и столбцов, называется минором k -го порядка.
. Определитель k- го порядка, составленный из элементов матрицы A, расположенных на пересечении выделенных строк и столбцов, называется минором k -го порядка.