
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА: Расчет соединения элементов деревянных конструкций: лобовая врубка.Стр 1 из 4Следующая ⇒
СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению практических работ для учащихся дневного и заочного отделения специальность 2-70 02 01 «Промышленное и гражданское строительство» Раздел 2 «Металлические конструкции»
Составила: Сипливая А.С., преподаватель Брестского государственного политехнического колледжа.
Методические указания обсуждены на заседании цикловой комиссии строительного отделения.
Протокол № ______ от «____»_________________2010 г.
Председатель ________Е.А. Миронюк
ПРАКТИЧЕСКАЯ РАБОТА № 6
ТЕМА: Расчет центрально-сжатой стойки. Расчет балки перекрытия. ЦЕЛЬ: Рассчитать центрально-сжатую стойку. Рассчитать балку перекрытия.
I. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1 Расчет центрально-сжатого элемента
1.1 Центрально сжатые элементы постоянного поперечного сечения следует рассчитывать по формулам: на прочность на устойчивость где fc ,0, d — расчетное сопротивление древесины сжатию вдоль волокон (см. таблицу 3, приложение 1); Ad — расчетная площадь поперечного сечения, принимаемая равной: — площади сечения брутто A sup, если ослабления не выходят на кромки и площадь ослабления не превышает 25 % площади брутто; — площади сечения нетто A inf с коэффициентом 4/3, если ослабления не выходят на кромки и площадь ослабления превышает 25 % площади брутто; — площади сечения нетто A inf, если ослабления выходят на кромки; kc — коэффициент продольного изгиба, определяемый по формуле (3) или (4). 1.2 При расчете центрально сжатых элементов на устойчивость следует учитывать упругую и упругопластическую работу древесины. Критические напряжения в указанных областях разделяются граничной гибкостью, которая в расчетах принята равной Коэффициент продольного изгиба следует определять по формуле (3) или (4), в зависимости от гибкости элемента:
где с = 0,8 для древесины и с = 1 для фанеры; С = 3000 для древесины и С = 2500 для фанеры. 1.3 Гибкость элементов цельного, постоянного по длине сечения определяется по формуле
где i — радиус инерции сечения элемента в направлении соответствующей оси. 1.4 Расчетную длину элемента
где l— свободная длина элемента. Гибкость элементов и их отдельных ветвей в деревянных конструкциях не должна превышать значений, указанных в таблице 2 (приложение 1)
Расчет изгибаемого элемента
2.1 Расчет изгибаемых элементов на прочность по нормальным напряжениям следует производить по формуле
где
Для элементов из цельной древесины При определении 2.2 Расчет изгибаемых элементов на прочность при скалывании следует производить по формуле
где
II ПРИМЕРЫ РАСЧЕТА Задача 1. Определить размеры квадратного поперечного сечения цельной центрально сжатой стойки длиной ld = 3,6 м. Материал – сосна 1-го сорта. Расчетное усилие, действующее на стойку с учетом коэффициента надежности по ответственности Nd = 380 кН (длительная). Класс условий эксплуатации - 3. Проверить устойчивость подобранного сечения стойки. Из условия устойчивости определяем площадь поперечного сечения
Задаёмся гибкостью элемента λ=70.
Определяем расчётное сопротивление сжатию.
По сортаменту пиломатериалов подбираем сечение 250×250. Определяем гибкость стойки:
Проверяем условие
7,6 МПа < 13,6МПа Окончательно принимаем сечение 250×250.
Задача 2. Подобрать прямоугольное сечение (соотношение сторон h/b =1,5) деревянной балки перекрытия жилого дома. Класс условий эксплуатации - 2. Материал балки – кедр сибирский 2 сорта. Расчетная длина балки – ld = 4,78 м. Нагрузка на погонный метр балки: qd = 5,65 кН/м (длительная). Выполнить проверку принятого сечения на скалывание.
Из условия прочности определяем требуемый момент сопротивления.
Определяем расчётный момент: Определяем расчётное сопротивление:
Выражаем ширину сечения балки:
принимаем сечение балки 150х225 мм Проверяем прочность на скалывание:
Определяем расчётное сопротивление древесины на скалывание: 0,6 МПа>1,37 МПа, прочность на скалывание обеспечена, окончательно принимаем сечение 150х225 мм.
III ЗАДАНИЕ ДЛЯ ПРАКТИЧЕСКОЙ РАБОТЫ
Задача№1 Определить размеры квадратного поперечного сечения цельной центрально сжатой стойки. Проверить устойчивость подобранного сечения стойки. Исходные данные принять по одному из вариантов таблицы 1.
Исходные данные к задаче Таблица 1
Задача№2 Подобрать прямоугольное сечение (соотношение сторон h/b =1,5) деревянной балки перекрытия жилого дома. Выполнить проверку принятого сечения на скалывание.
Исходные данные принять по одному из вариантов таблицы 2.
Исходные данные к задаче Таблица 2
Контрольные вопросы.
1. Какая древесина применяется для изготовления несущих конструкций? 2. Как определяется расчетное сопротивление древесины? 3. В каком случае сжатые деревянные элементы рассчитываются только по прочности, а в каком по прочности и устойчивости? 4. Чему равны значения предельной гибкости для основных сжатых элементов, второстепенных сжатых, растянутых? 5. По каким нагрузкам выполняются расчеты изгибаемых элементов по предель- ным состояниям первой группы? 6. Запишите условие прочности изгибаемых элементов. 7. Запишите условие устойчивости центрально-сжатого элемента. 8. Как определить расчетную длину центрально-сжатого элемента?
ПРАКТИЧЕСКАЯ РАБОТА № 7 II ПРИМЕР РАСЧЕТА Рассчитать и запроектировать опорный узел треугольной стропильной фермы, выполненной лобовой врубкой с одним зубом. Пояса фермы выполнены из брусьев (
Расчетное растягивающее усилие в нижнем поясе
Nd2 = N d1 · cos α=40 · 0,89=35,6кН(длительное). 1.Требуемая несущая способность лобовой врубки из условия смятия древесины Rcm,d = fcm,a,d ·Ac, должна быть не менее Nd1=40 кН.
Расчетное сопротивление смятию fсm,о,d =fсm,о,d · kmod · kx = 15 · 0,95· 1 = 14.25 МПа fcm,90,d = fcm90,d · kmod · kx = 3 · 0,95· 1 =2.85МПа
Исходя из этого площадь смятия
Из формулы (3) определяем глубину врубки Принимаем h1=3см, тогда hw= 3 h1 = 3 ·3 = 9см.
Так как h1< hw/3 принимаем глубину врубки h1= hw/3. Окончательно сечение брусьев Т.к. сечения элементов определялось из условия смятия, то прочность на смятие обеспечена.
2.Определим несущую способность лобовой врубки из условия скалывания (5) fv,о,d = fv,о,d · kmod · kx = 2.1 · 0.95· 1 = 1.995 МПа
Из условия (1) определяем
Окончательно принимаем
Av=b · lv= 15 · 25 = 375 см2 Rνd = 0,978·375 = 36,67кН > Nd2=35,6 кН. Следовательно, несущая способность лобовой врубки из условия скалывания обеспечена.
3. Проверка несущей способности нижнего пояса на разрыв по ослабленному сечению (9) σt,о,d = N d / Аi nf ≤ ft,о,d ft,о,d = ft,о,d · kmod · kx =7.0 · 0.95·1 = 6.65МПа Аinf = Аsup – Аосл = 15 · 12,5 – 15 ·3 = 142,5 см2. Для обеспечения несущей способности должно выполняться условие N d> Nd2 N d = ft,о,d··Аi nf = 0.665 ·142,5 = 94,76 кН > Nd2 =35,6кН Прочность нижнего пояса по ослабленному сечению на разрыв обеспечена.
III ЗАДАНИЕ ДЛЯ ПРАКТИЧЕСКОЙ РАБОТЫ
Рассчитать и запроектировать опорный узел треугольной стропильной фермы, выполненной лобовой врубкой с одним зубом. Пояса фермы выполнены из брусьев. Исходные данные принять по одному из вариантов таблицы 1.
Таблица 1 Исходные данные к задаче
Контрольные вопросы 1. Какие вы знаете соединения элементов деревянных конструкций? 2. Какое соединение называется врубкой? 3. Расскажите конструктивные требования к решению врубки. 4. Как определяется расчетная несущая способность соединения на смятие? 5. Как определяется расчетная несущая способность соединения на скалывание? 6. Расскажите о назначении аварийного болта. ПРАКТИЧЕСКАЯ РАБОТА № 8
Проверка на прочность Обрешетку рассматриваем как двухпролетную неразрезную балку с пролетом l=B=110 см. Наибольший изгибающий момент равен: а) для первого сочетания нагрузок (собственный вес и снег):
Рис. 2 Расчетная схема настила при первом сочетании нагрузок
б) для второго сочетания нагрузок (собственный вес и монтажная нагрузка):
Рис. 3 Расчетная схема настила при втором сочетании нагрузок
где Так как
Так как плоскость действия нагрузки не совпадает с главными плоскостями сечения бруска, то брусок рассчитываем на косой изгиб. Составляющие изгибающего момента относительно главных осей бруска равны:
Моменты сопротивление и инерции сечения следующие:
Наибольшее напряжение:
Определяем запас прочности:
здесь fm,d=13 МПа=1,3 кН/см2 – расчетное сопротивление изгибу для элементов настила из древесины сосны 3-го сорта (см приложение 2); kmod=1,05 – коэффициент условий работы для 3 класса условий эксплуатации при учёте полной снеговой нагрузки (табл.5 приложение 1); gn=0,95 – коэффициент надежности по назначению для II класса ответственности здания (приложение 3). Проверка на жесткость Определяем прогиб от нормативной нагрузки в плоскости, перпендикулярно скату:
Определяем прогиб от нормативной нагрузки в плоскости, параллельно скату:
где: Fk=0,134 кН/м=0,0013 кН/см – полная нормативная нагрузка (см. табл. 1); Е0=104´kmod=0,85´104´0,95=0,81´104 МПа=0,81´103 кН/см2 – модуль упругости древесины вдоль волокон в соответствии с приложением 2; 1/121,5 – предельный относительный прогиб для ld=1,1 м, табл.8 приложения 1. Полный прогиб:
Принятые при расчете размеры доски для выполнения обрешетки, пригодны в использовании. Т.к. прочность и прогиб доски удовлетворяет нормативным требованиям и они не велики при заданных классах условий эксплуатации и ответственности здания, уменьшить их мы не можем из-за требований предъявленных компанией «РАННИЛА-МОНТЕРЕЙ».
III ЗАДАНИЕ ДЛЯ ПРАКТИЧЕСКОЙ РАБОТЫ
Рассчитать и запроектировать опорный узел треугольной стропильной фермы, выполненной лобовой врубкой с одним зубом. Пояса фермы выполнены из брусьев. Исходные данные принять по одному из вариантов таблицы 1.
Таблица 1 Исходные данные к задаче
Контрольные вопросы
1. Древесина какого сорта применяется для изготовления деревянных настилов? 2. На сколько опор должны опираться доски настилов? 3. Как принимается снеговая нагрузка при расчете настилов и обрешеток? 4. Что представляет собой расчетная схема: а) настила или обрешетки; б) стропильных ног? 5. На какие два сочетания нагрузок рассчитываются настилы и обрешетки и как определяются расчетные изгибающие моменты? 6. По какой формуле определяется относительный прогиб?
Приложение 1 Таблица 1 –значение коэффициента m0
Таблица 2- предельная гибкость элементов lmax
Примечания 1)Расчетные сопротивления, приведенные в таблице 3, следует умножать на коэффициенты условий работы: для различных условий эксплуатации и продолжительности действия нагрузок — на значения коэффициента k mod, указанные в таблице 5; 2) Расчетные сопротивления древесины сосны (кроме веймутовой), ели, лиственницы европейской приведены в таблице 3. Расчетные сопротивления для других пород древесины устанавливаются путем умножения значений, приведенных в таблице 3, на переходные коэффициенты kх, указанные в таблице 4. Таблица 3 — Расчетные сопротивления древесины
Таблица 4 — Значения коэффициента kх для породы древесины
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.254.0 (0.141 с.) |

 (1)
(1) (2)
(2) = 70.
= 70. при
при  (3)
(3) при
при  (4)
(4) , (5)
, (5) — расчетная длина элемента;
— расчетная длина элемента;
 (6)
(6) — коэффициент, определяемый в соответствии с требованиями таблице 1(приложение 1);
— коэффициент, определяемый в соответствии с требованиями таблице 1(приложение 1); , (7)
, (7) — расчетный изгибающий момент;
— расчетный изгибающий момент; — расчетное сопротивление изгибу(см. таблицу 3, приложение 1);
— расчетное сопротивление изгибу(см. таблицу 3, приложение 1); — расчетный момент сопротивления поперечного сечения элемента.
— расчетный момент сопротивления поперечного сечения элемента. .
. ослабления сечений, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном расчетном сечении.
ослабления сечений, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном расчетном сечении.
 , (8)
, (8) — расчетная поперечная сила;
— расчетная поперечная сила; — статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;
— статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси; — момент инерции брутто поперечного сечения элемента относительно нейтральной оси;
— момент инерции брутто поперечного сечения элемента относительно нейтральной оси; — расчетная ширина сечения элемента;
— расчетная ширина сечения элемента; — расчетное сопротивление древесины скалыванию при изгибе(см. таблицу 3, приложение 1).
— расчетное сопротивление древесины скалыванию при изгибе(см. таблицу 3, приложение 1).


 , c=0,8 для древесины
, c=0,8 для древесины





 49,8<70 определяем коэффициент продольного изгиба
49,8<70 определяем коэффициент продольного изгиба






 из соотношения сторон принимаем 1,5b=h следовательно
из соотношения сторон принимаем 1,5b=h следовательно 
 мм
мм





 ). Угол между поясами α= 27° (sin α = 0,45; cos α= 0,89). Расчетное сжимающее усилие в верхнем поясе Nd1 = 40 кН(длительное). Материал древесины сосна 2 сорта, влажность 12%. Класс условиэксплуатации-2
). Угол между поясами α= 27° (sin α = 0,45; cos α= 0,89). Расчетное сжимающее усилие в верхнем поясе Nd1 = 40 кН(длительное). Материал древесины сосна 2 сорта, влажность 12%. Класс условиэксплуатации-2



 , что соответствует сортаменту пиломатериалов.
, что соответствует сортаменту пиломатериалов.



 .
.
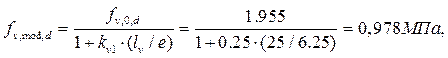





 - сосредоточенная нагрузка;
- сосредоточенная нагрузка; ,толщину настила определяем при втором сочетании нагрузок, где:
,толщину настила определяем при втором сочетании нагрузок, где: - коэффициент условий работы для 3 класса условий эксплуатации при учёте полной снеговой нагрузки (табл.5 приложение 1);
- коэффициент условий работы для 3 класса условий эксплуатации при учёте полной снеговой нагрузки (табл.5 приложение 1); - коэффициент условий работы для 3 класса условий эксплуатации при учёте кратковременного действия монтажной нагрузки (табл.5 приложение 1).
- коэффициент условий работы для 3 класса условий эксплуатации при учёте кратковременного действия монтажной нагрузки (табл.5 приложение 1).





 <
< 
 <1 (запас прочности составляет 24%), где
<1 (запас прочности составляет 24%), где
 ,
,
 <
< 
 где коэффициент
где коэффициент  принимают по таблице 7.1.
принимают по таблице 7.1.



