
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое определение вероятности.Стр 1 из 2Следующая ⇒
Лекция 1. Основные понятия теории вероятности. (ТВ)- СС-1 ТВ – это раздел математики изучающий закономерности случайных явлений. «ТВ объединяет точность математических доказательств с неопределённостью случая и примеряет эти противоречивые элементы». Испытание - модель реального действия, реализация определённого комплекса условий, который может быть воспроизведён сколько угодно раз. Задать испытание в т/в это значит задать множество его элементарных (неделимых на более мелкие) исходов W. W= Случайное событие - событие которое может наступить или не наступить в результате испытания. Для любого события “А” множество W элементарных событий разделяется на два подмножества W: А+ и А– . А+ - подмножество благоприятных исходов вместе с каждым из которых наступает событие А+. А– - подмножество неблагоприятных исходов, при реализации которых событие А не происходит. Задать событие– это значит задать подмножество А+ благоприятных исходов на множестве W. Невозможное событие - событие которое никогда ни происходит в результате испытания. Достоверное событие - событие которое всегда происходит при испытании. Два события называются несовместными, если появление одного исключает появление другого. События совместны, если они могут произойти одновременно. Вероятность случайного события - это количественная мера степени уверенности в его наступлении. Классическое определение вероятности: Для испытания с конечным числом равновозможных исходов вероятность случайного события “A” обозначается Р(А) и определяется как отношение числа благоприятных исходов m к общему числу n элементарных исходов испытания: Р(А) = m/n. Вероятность случайного события принимает значения от 0 до 1. 0 Вероятность невозможного события равна 0. Вероятность достоверного события равна 1. Формула полной вероятности. Пусть появление некоторого события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами. Тогда вероятность события А равна сумме попарных произведений вероятности каждой из этих гипотез Вi на соответствующую условную вероятность появления события А.
Формулы Байеса. Пусть появление в некотором испытании события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами.
Тогда, зная вероятности гипотез Р(Вi) до проведения испытания, мы можем переоценить их после проведения испытания, в результате которого появилось событие А.
где Р(Вi) – вероятности гипотез, известные до испытания (априорные вероятности гипотез),
Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. По формуле Байеса можно более точно пересчитывать вероятность, принимая во внимание как ранее известную информацию (априорные данные), так и данные новых наблюдений (апостериорные данные). Вычисление вероятностей событий в серии независимых испытаний. Схема Бернулли - последовательность независимых испытаний (т.е. таких испытаний, вероятность исходов которых не зависит ни от номера испытания, ни от результатов предшествующих испытаний) с двумя возможными исходами. Вероятность первого исхода - А, называемого успехом, в каждом испытаний равна р, тогда вероятность второго исхода – неуспеха, равна разности единицы и р: Р(А)=р Р( Формула Бернулли Вероятность, что в серии из n испытаний по схеме Бернулли,событие А, произойдёт ровно k раз:
р – вероятность наступления события А в одном испытании, Теорема Лапласа: применяется при больших значениях n, когда формулу Бернулли использовать сложно. Пусть Р(А)=р – вероятность проявления события А в одном испытании, тогда вероятность, что в серии из n независимых испытаний событие А произойдёт точно k раз приблизительно вычисляется по формуле Лапласа:
Интегральная теорема Лапласа. – позволяет определить вероятность того, что событие А в n независимых испытаниях произойдёт не менее
Значения функций Закон Пуассона распределения вероятностей массовых и редких событий.
где Формула Пуассона применяется, когда n – очень велико, а р – достаточно мало. Лекция 4. Случайные величины. СВ-1. Случайная величина это функция, определённая на множестве случайных событий. Случайная величина в результате эксперимента принимает те или иные числовые значения, зависящие от случайных причин. Примеры: кубик, 2 монеты, рост, вес, количество успехов и т.д.. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина это случайная величина, все возможные значения которой изолированы друг от друга. Множество значений ДСВ – конечное или счётное множество. Непрерывная случайная величина – это СВ, возможные значения которой заполняют некоторый конечный или бесконечный интервал. Множество её значений имеет мощность континуума. Дискретные СВ. Закон распределения дискретной случайной величины – соответствие между всеми возможными значениями данной случайной величины и их вероятностями. Способы задания: графический, аналитический (
Значения СВ
Функция распределения случайной величины – равна вероятности, что случайная величина примет значение меньше, чем данное. График – ступенчатая возрастающая функция.
Свойства дисперсии. 1) Постоянный множитель можно вынести за знак дисперсии, возводя его в квадрат. 2) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин. 2) Дисперсия постоянной величины равна 0. Доказательство: Д(С) = М((С۰М(С))2) = М(С – С)2 = М(02) = М(0) = 0 3) Дисперсия суммы двух зависимых случайных величин: D( Ковариация двух случайных величин:
Коэффициент корреляции -
Ковариация и корреляция
Лекция 6а. Примеры дискретных распределений: СВ2 1) Равномерное дискретное распределение на множестве натуральных чисел
2) Геометрическое распределение с параметром р (0<p<1).
3) Биномиальное распределение:
4) Распределение Пуассона: Теорема Ляпунова. Если случайная величина равна сумме очень большого числа взаимно независимых случайных величин, влияние каждой из которых на сумму ничтожно мало, то эта случайная величина имеет распределение, близкое к нормальному. На практике, нормально распределённой считают величину, равную сумме более чем 10 случайных величин с произвольными законами распределения.
Лекция 1. Основные понятия теории вероятности. (ТВ)- СС-1 ТВ – это раздел математики изучающий закономерности случайных явлений. «ТВ объединяет точность математических доказательств с неопределённостью случая и примеряет эти противоречивые элементы». Испытание - модель реального действия, реализация определённого комплекса условий, который может быть воспроизведён сколько угодно раз. Задать испытание в т/в это значит задать множество его элементарных (неделимых на более мелкие) исходов W. W= Случайное событие - событие которое может наступить или не наступить в результате испытания. Для любого события “А” множество W элементарных событий разделяется на два подмножества W: А+ и А– . А+ - подмножество благоприятных исходов вместе с каждым из которых наступает событие А+. А– - подмножество неблагоприятных исходов, при реализации которых событие А не происходит. Задать событие– это значит задать подмножество А+ благоприятных исходов на множестве W. Невозможное событие - событие которое никогда ни происходит в результате испытания. Достоверное событие - событие которое всегда происходит при испытании. Два события называются несовместными, если появление одного исключает появление другого. События совместны, если они могут произойти одновременно. Вероятность случайного события - это количественная мера степени уверенности в его наступлении. Классическое определение вероятности: Для испытания с конечным числом равновозможных исходов вероятность случайного события “A” обозначается Р(А) и определяется как отношение числа благоприятных исходов m к общему числу n элементарных исходов испытания: Р(А) = m/n. Вероятность случайного события принимает значения от 0 до 1. 0 Вероятность невозможного события равна 0. Вероятность достоверного события равна 1. Статистическое определение вероятности. Относительная частота события А -отношение числа наступления события А в серии изn испытаний к общему числу испытаний n. Если в различных сериях из n испытаний относительная частота m(А)/n события мало изменяется и близка некоторому числу Р, то это число считают статистической вероятностью. Геометрическое определение вероятности - Применяется к испытанию с бесконечным числом равновозможных исходов. Пусть дан отрезок длины “L” и на нём отрезок “L1” Под геометрической вероятностью принимается вероятность попадания точки на отрезок L1, равная отношению длин этих отрезков Р(А) = L1/L
Комбинаторика – это раздел математики в которой изучаются расположения (комбинации) объектов составленные по определённым правилам и способам подсчёта этих комбинаций. Основными расположениями объектов являются: перестановки размещения и сочетания. Основное правило комбинаторики: если элемент а1 можно выбрать “n1” способами и при каждом таком выборе, выбор элемента а2 может быть произведён n2 способами, то общее число пар (а1;а2) равно N = n1۰n2. Перестановками называют упорядоченное множество составленное из всех элементов “A”. Перестановки отличаются друг от друга порядком элементов. Рn – число перестановок множества из n элементов = n۰(n – 1)۰(n – 2)…1 = n!; (0! = 1; 1! = 1; 2! = 2; 3! = 6…). Размещения. Ank упорядоченныеk- элементные подмножества n элементного множества. Число размещений: Ank=n(n-1)(n-2)۰…۰(n – k + 1)= Сочетания Cnk - “k” элементные подмножества “n” элементного множества. Два сочетания отличаются друг от друга только составом элементов, но не их порядком. Связь между числом сочетаний, размещений и перестановок. Ank = Cnk۰Pk Число сочетаний: Cnk =Ank/Pk = Свойства числа сочетаний: 1). Cnk = Cnn – k; 2). Cnk = Cn – 1 k – 1 + C k n – 1 Лекция 2. Основные теоремы теории вероятности. СС-2 События “A” и “B” связанные с одним и тем же испытанием, называются эквивалентными, если их множества благоприятных исходов А+ и В+ совпадают. Вероятности эквивалентных событий равны Р(А) = Р(В). – Операции над событиями – Противоположным событием для события “A” называется новое событие - (Событие Суммой или объединением двух событий А и В называется новое событие С=А+В =А Если события А и В несовместные, то сумма А+В заключается в появлении одного из них. Произведением или пересечением двух событий А и В называется новое событие С=А۰В =А∩В, заключающееся в одновременном наступлении событий А и В. – Свойства операций над событиями – 1). Коммутативность сложения А + В = В + А. 2). Ассоциативность сложения (А + В) + С = А + (В + С). 3). Коммутативность умножения А۰В = В۰А. 4). Ассоциативность умножения (А۰В)С = А(В۰С). 5). Сумма противоположных событий – достоверное событие. 6). Произведение противоположных событий, есть невозможное событие.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.0.25 (0.058 с.) |
 .
. Р(А)
Р(А)  1
1
 ,
, - вероятности гипотез, вычисленные после проведения испытания, при условии, что событие А произошло (апостериорные вероятности гипотез); Р(А) – полная вероятность события А,
- вероятности гипотез, вычисленные после проведения испытания, при условии, что событие А произошло (апостериорные вероятности гипотез); Р(А) – полная вероятность события А, — вероятность наступления события А при истинности гипотезы Вi.
— вероятность наступления события А при истинности гипотезы Вi.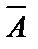 )=1-р=q.
)=1-р=q. , где
, где  число сочетаний из “n” элементов по “k” элементов в каждом.
число сочетаний из “n” элементов по “k” элементов в каждом. –вероятность не наступления события А в одном испытании, n – общее число испытаний, k – число успехов в серии из n испытаний.
–вероятность не наступления события А в одном испытании, n – общее число испытаний, k – число успехов в серии из n испытаний. , где
, где  ; где
; где  ,
,  .
. и не более
и не более  раз.
раз. , где
, где  ,
,  ;
; 
 и
и  приводятся в таблицах (см тб. 1 и 2)
приводятся в таблицах (см тб. 1 и 2) -вероятность того, что в серии из n испытаний «успех» произойдёт ровно k раз.
-вероятность того, что в серии из n испытаний «успех» произойдёт ровно k раз. , n – общее число независимых испытаний, р – вероятность «успеха» в одном испытании.
, n – общее число независимых испытаний, р – вероятность «успеха» в одном испытании. ) и табличный.
) и табличный.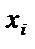



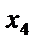







 ,
, =1. (при n
=1. (при n 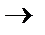
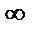 , этот ряд сходится к единице)
, этот ряд сходится к единице)
 ,
, 
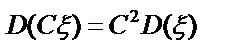
 , если
, если  , то эта случайная величина равна константе почти наверняка (с вероятностью 1)
, то эта случайная величина равна константе почти наверняка (с вероятностью 1) )=D(
)=D( )+D(
)+D( )+ 2M(
)+ 2M( -M(
-M(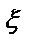 ))(
))( -M(
-M( ))
))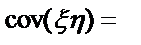 M((
M(( независимы
независимы 
 0
0

 не коррелируют
не коррелируют
 =
= 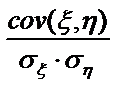 -безразмерная величина, показатель «тесноты» зависимости между случайными величинами.
-безразмерная величина, показатель «тесноты» зависимости между случайными величинами.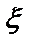 с
с  M(
M( -M
-M 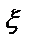 )(
)( -M
-M  )=D(
)=D(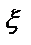 );
); =
= 
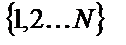
 ;
;  ; М(
; М( )=
)= 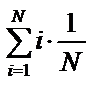
 ,
,  ; М(
; М( )=
)=  ; М(
; М( )=
)=  .
. ,
,  ; М(
; М( ,
,  ; М(
; М( )=
)=  ; М(
; М( )
) 


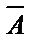 , состоящее в том, что событие “A” не произошло.
, состоящее в том, что событие “A” не произошло. В, которое состоит в том, что произошло хотя бы одно из этих событий (или событие А, или В или А и В одновременно).
В, которое состоит в том, что произошло хотя бы одно из этих событий (или событие А, или В или А и В одновременно).




