
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 5. Задача о беспорядках ⇐ ПредыдущаяСтр 5 из 5
Пусть имеется конечное упорядоченное множество элементов {1,…, n }. Из этих элементов могут быть образованы перестановки a 1,…, an (ai Î{1,…, n }). Число всех возможных перестановок – n!. Среди этих n! перестановок есть такие, что ни один элемент не стоит на своём месте (ai ¹ i, i = Число беспорядков из n элементов обозначается Dn (ясно, что Dn<n!). Теорема. Число беспорядков из n элементов равно:
# Обозначим через свойство pi – «i -й элемент стоит на i -м месте». Тогда по формуле решета Общее число перестановок n элементов – n! Число перестановок, где i -й элемент стоит на i -м месте, равно (n -1)! (ставим i -й элемент на i -е место, а оставшиеся n -1 элементы переставляем (n -1)! способами). При этом сам i -й элемент можно выбрать Число перестановок, где i -й элемент стоит на i -м месте, а j -й на j -м (i ¹ j), равно (n -2)!, при этом i -й и j -й элементы можно выбрать Аналогично, число перестановок, где на своих местах стоят хотя бы три элемента – Следствие 1. Так как то Следствие 2. Так как
Следствие 3. Рекуррентная формула для числа беспорядков: #
Следствие 4. # По рекуррентной формуле из следствия 3 получаем
Следствие 5. Ещё одна рекуррентная формула для числа беспорядков: # Рассмотрим n элементов x 1, x2, …, xn. Переставим их так, чтобы получить беспорядок. Начнём с x 1: возьмём x 1 и подставим его на место i -го элемента (i ¹1). Тогда xi можно поставить на либо на первое место, либо на какое-то другое, кроме i- го. Если x 1 стоит на i -м месте, а xi – на 1-ом, то число таких беспорядков – Dn -2 (т.е. число беспорядков оставшихся n -2 элементов). Если x 1 не стоит на первом месте, то такой беспорядок определяется условием:
x 2 не стоит на 2-м месте, x 3 не стоит на 3-м месте, … xi -1 не стоит на (i -1)-м месте, xi не стоит на 1-м месте, xi+ 1 не стоит на (i +1)-м месте, … xn не стоит на n -м месте. Всего здесь n -1 элемент, то есть число таких беспорядков – Dn -1. Итак, если x 1 стоит на i -ом месте, то число таких беспорядков Dn -1+ Dn-2. Но x 1 можно поставить на любое из (n -1) мест (кроме 1-го). Для каждой установки x 1 справедливы приведённые выше рассуждения. Таким образом, общее число беспорядков – (n -1)(Dn- 1+ Dn-2). #
Для проверки полученной формулы вычислим количество беспорядков для некоторых значений n по рекуррентной и прямой формулам. По следствию 4, D 0=1, D 1=0.
Для строгого доказательства правильности рекуррентной формулы, проверим ее в общем виде.
Из следствия 3
Обозначим через Dn,r число перестановок, в которых на своих местах остаются r элементов, а остальные (n-r) образуют беспорядок. Ясно, что Dn,n =1 (все элементы на своих местах), и Dn,0=Dn (ни одного элемента нет на своём месте). Теорема. # r элементов, стоящих на своём месте, можно выбрать из n элементов С другой стороны, (n-r) элементов, образующих беспорядки, можно выбрать
Пример. Выстраиваем 5 человек в определённом порядке, после чего 3 из них переставляем так, чтобы они не стояли на своих местах. Сколько таких перестановок? Ответ: если трое не стоят на своих местах, то оставшиеся двое стоят на своих местах, т.е.
Следствие. # Из n элементов можно образовать n! перестановок без повторений. Среди них будет Dn,0 таких, где ни один элемент не стоит на своём месте; Dn ,1 таких, где по одному элементу стоит на своём месте; Dn ,2 таких, где по паре элементов стоит на своих местах;
и т.д.; Dn,n =1 таких, где все элементы стоят на своих местах. Следовательно, общее число перестановок (n!) равно сумме этих чисел. #
Функция Эйлера Функция Эйлера φ (n), где n – натуральное число, дает количество натуральных чисел, не превышающих n и взаимно простых с n. Иначе говоря, φ (n)= k, где 0< k £ n; (k, n)=1. Теорема
# В теореме Лежандра заменим ai на pi, где pi – простые делители n. Тогда По теореме Лежандра
Пример. Определим, сколько чисел, не превышающих 100, взаимно простые с 100. Разложим число 100 на простые сомножители: 100=2·2·5·5=2252. Таким образом, у числа 100 два простых делителя – 2 и 5. По формуле Эйлера получаем
Таким образом, среди первой сотни есть 40 чисел, взаимно простых с 100. Функция Мебиуса Функция Мебиуса m (n), где n – натуральное число, принимает следующие значения:
Функция Мебиуса позволяет записать функцию Эйлера в виде суммы:
Суммирование идет по всем делителям n (а не только по простым делителям).
Пример. Вычислим φ (100), используя функцию Мебиуса. Все делители 100 – {1, 2, 4, 5, 10, 20, 25, 50, 100}. m (1) = 1, m (2) = (-1)1 = -1 (у двойки один простой делитель – 2) m (4) = 0 (4 делится на квадрат двойки) m (5) = (-1)1 = -1 (у 5 один простой делитель – 5) m (10) = (-1)2 = 1 (у 10 два простых делителя – 2 и 5) m (20) = 0 (20 делится на квадрат двойки) m (25) = 0 (25 делится на квадрат пятерки) m (50) = 0 (50 делится и на 22, и на 55) m (100) = 0 (100 делится и на 22, и на 55) Таким образом,
Свойство функции Мебиуса: Например, n =100, a Î{1, 2, 4, 5, 10, 20, 25, 50, 100}.
Шаг 1: Вводим обозначения – обозначим число r-сочетаний с повторениями из n-множества S через f(n,r) Шаг 2: Начальные условия: f(n,1)=n; f(1,r)=1 Шаг 3: Логические рассуждения Как правило, из множества S выделяется какой-либо элемент и фиксируется. Чаще всего – первый из ряда. Тогда относительно нашего случая о любом r-сочетании с повторениями, можно сказать, содержит оно фиксированный элемент или не содержит. Если содержит, то остальные (r-1) элементов этого r-сочетания (а, значит, r-сочетаний содержащих фиксированный элемент), можно выбрть f(n, r-1) способом. Если сочетание не содержит, то таких r-сочетаний f(n-1,r). Т.к. эти случаи взаимно исключают друг друга, то: f(n,r)= f(n, r-1)+ f(n-1,r) Шаг 4: Необходимо проверить получившуюся рекуррентную формулу применительно к известному результату. f(n,0)=1=f(n,1)-f(n-1,1)=n-(n-1) Шаг 5: Различные построения. Один из вариантов: последовательно вычислять f(n,2), f(n,3) и т.д. и смотреть есть ли закономерность. f(n,2)=n(n+1)/2 f(n,3)=n(n+1) (n+2)/6 В общем виде: f(n,r)=n(n+1)(n+2)….(n+r-1)/r! Шаг 6: Рекуррентный спуск Проверка с помощью формулы начальных условий: f(n,1)=n f(1,r)=1
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 2448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.136.170 (0.047 с.) |
 ). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n -м месте. Такие перестановки называются беспорядками.
). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n -м месте. Такие перестановки называются беспорядками. .
. .
. способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно
способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно  .
. способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –
способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –  .
. . Число перестановок, где на своих местах стоят хотя бы r элементов –
. Число перестановок, где на своих местах стоят хотя бы r элементов –  . Число перестановок, где все элементы стоят на своих местах
. Число перестановок, где все элементы стоят на своих местах  . Подставляем в формулу решета:
. Подставляем в формулу решета:  #
# ,
, .
. , то
, то  .
. .
.
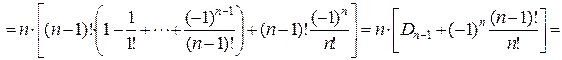
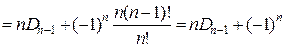 #
#
 или
или  . При n =1 получаем
. При n =1 получаем 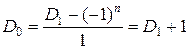 . По формуле из следствия 1 получаем
. По формуле из следствия 1 получаем  . Следовательно,
. Следовательно, 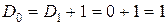 . #
. # .
.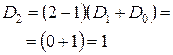

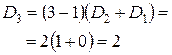

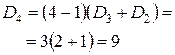

 .
. . Тогда
. Тогда . Подставим этот результат в рекуррентную формулу:
. Подставим этот результат в рекуррентную формулу: . Получили формулу из следствия 3.
. Получили формулу из следствия 3. .
. способами. Для каждой такой выборки остальные (n-r) элементов образуют беспорядки, число которых Dn-r. Следовательно, всего таких перестановок
способами. Для каждой такой выборки остальные (n-r) элементов образуют беспорядки, число которых Dn-r. Следовательно, всего таких перестановок  .
.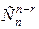 способами. Следовательно,
способами. Следовательно,  . В силу симметричности биномиальных коэффициентов
. В силу симметричности биномиальных коэффициентов 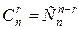 , обе формулы дают один и тот же результат.
, обе формулы дают один и тот же результат. #
#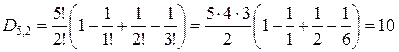 .
. .
.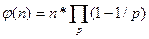 , где n- натуральное число, p-простые делители числа n. Выразить функцию Эйлера через функцию Мебиуса.
, где n- натуральное число, p-простые делители числа n. Выразить функцию Эйлера через функцию Мебиуса.  , где pi – все простые делители n. (
, где pi – все простые делители n. (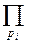 - произведение по всем простым делителям числа n).
- произведение по всем простым делителям числа n). (так как pi делят n нацело).
(так как pi делят n нацело).
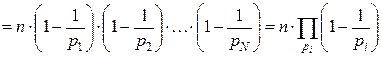 . #
. # .
.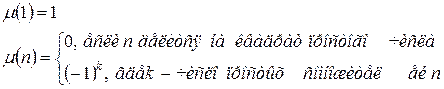
 .
.
 .
. .
.


