
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 4. Число сочетаний с повторениями
Число r -сочетаний с повторениями из n -множества равно
# 1 способ – доказательство Эйлера. Пусть дано n -множество S. Пронумеруем все его элементы, т.е. множеству S взаимно однозначно поставим в соответствие множество S’: S «S’ ={1, …, n } – номера элементов из S. Тогда r -выборке из S однозначно соответствует выборка r натуральных чисел из S’. Т.к. в сочетании порядок не важен, r -выборку натуральных чисел можно расположить так, чтобы a 1 £ a 2£ … £ ar (1) (где ai – выбранное натуральное число). Между числами стоит знак £, т.к. выборка с повторениями и числа могут повторяться (например, а2 и а3 могут быть одним и тем же числом). Добавим в выборке (1) к а1 ноль, к а2 – 1, к а3 – 2 и т.д., т.е. получим выборку a 1+0 < a 2+1 < … < ar+r -1 (2) Выборка (2) взаимно однозначно соответствует выборке (1), причём в ней нет одинаковых чисел (неравенство строгое). Следовательно, выборка (2) – это r -выборка без повторений из множества S’’` ={1, …, n, n +1, n +2, …, n+r -1}, S’’ - (n+r -1)-множество. Таким образом, Эйлер свёл задачу о числе r -сочетаний с повторениями из n -множества к числу r -сочетаний без повторений из (n+r -1)-множества.
Число упорядоченных (r1,r2,…,rk) – разбиений n-множества равно Pn(r1,r2,…,rk):
По теореме о числе сочетаний без повторений и обобщенному правилу произведения имеем, что:
Интерпретации: 1) r-сочетания из n-множества Pn(n-r,r) 2) Pn(1,1,1,1…,1) – перестановка
Абстракция – большинства комбинаторных задач изложено с использованием этой интерпретации
Операция размещения представляет собой по существу функциональное отношение, с которым связывают функцию f, область определения, которая является множеством N, а область значений множество N. Такое соответствие в современной математике называют отображением и обозначают <N,K,f>
Виды: Map (N,K)= {f:N -> K, f - произвольная} N в K Усл. сущ.: Map (N,K)!= 0 всегда
Sur (N,K)= {f:N -> K, f – сюрьективное} N на K Усл. сущ.: Sur (N,K)!= 0 => |N|>=|K|
Inj (N,K)= {f:N -> K, f - инъективное} Усл. сущ.: Inj (N,K)!= 0 => |N|=<|K|
Bij (N,K)= {f:N -> K, f - биективное} взаимнооднозначное отношение Усл. сущ.: Inj (N,K)!= 0 => |N|=|K|
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.203.172 (0.006 с.) |
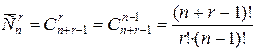 .
. .
.



