
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм минимальной раскраски вершин (ребер) графа G ⇐ ПредыдущаяСтр 6 из 6
Рассмотрим алгоритм определения хроматического числа h(G) (хроматического класса H(G)) графа G. 1. Выделяем множество вершинно пустых (реберно пустых) подграфов графа G. 2. Строим двумерную таблицу, каждой строек которой сопоставим взаимно однозначно пустой подграф, столбцу – вершину (ребро); в клетке (i, j) записываем единицу, если j-ая вершина (j – ое ребро) содержится в i-ом пустом подграфе, в противном случае клетку оставляем пустой. 3. Определяем покрытие столбцов строками. Каждое покрытие порождает раскраску. Покрытие минимальной мощности определяет хроматическое число (хроматический класс) графа G. Пример 3. Определить хроматическое число графа G (рис. 2.3).
1 2 3 4 5 6 7 1. {1,3,5} 1 1 1 2. {1,5,7} 1 1 1 3. {1,4,7} 1 1 1 4. {2,4,7} 1 1 1 5. {2,5,7} 1 1 1 6. {2,4,6} 1 1 1 7. {3,6} 1 1 Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1,4,7. Значит h(G) = |{{1,3,5} {2,4,7}, {3,6}}| = 3. Зададимся красками: для множества вершин {1,3,5} - краска а, для множества вершин {2,4,7} - краска b, для множества вершин {3,6} - краска с. Раскрасим вершины графа G (рис. 2.6). 2 b
5 a G Рис. 2.6 Отметим, что вершину 3 можно раскрасить в две краски: а или с. Сравним значение хроматического числа h(G) с оценками этого числа (пример 1). Видно, что т. 2.2 и т. 2.3 дали для заданного графа G хорошее приближение, а т.2.4 – удовлетворительное приближение.■ Пример 4. Определить хроматический класс H(G) графа G, у которого V = {1,2,3,4,5,6,7}, U= {(1,2),(1,6), (2,3), (3,4),(3,7) (4,5),(5,6), (6,7)}.
5
Ø Ø Ø Ø Ø Ø Ø Ø
E1 E2 E3 E4 E5 E6 E7 E9
Рис. 2.7 Строим двумерную таблицу: A b c d e f g k 1. {a,c,e} 1 1 1 2. {a,c,g} 1 1 1 3. {a,d,g} 1 1 1
4. {a,d,k} 1 1 1 5. {a,e,k} 1 1 1 6. {b,d,f} 1 1 1 7. {b,d,g} 1 1 1 8. {b,e} 1 1 9. {d,f,k} 1 1 1 10. {c,f} 1 1 Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1,7,9. Значит Н(G) = |{{a,c,e},{b,d,g}, {d,f,k}} | = 3. Зададимся красками: {a,c,e} - краска I, {b,d,g} – краска II, {d,f,k} – краска III. Раскрасим ребра заданного графа G (рис. 2.8)
A b
e d
G Рис. 2.8 Отметим, что ребро d можно раскрасить в два цвета.■ Пример 5. Показать, что хроматический класс Н(G) графа G (рис. 5а) равен хроматическому классу h(
Найдем хроматическое число h( Выделяем вершинно пустые подграфы графа
5
E8 E10
Ø Ø Ø Ø Ø Ø Ø Ø
E1 E2 E3 E4 E5 E6 E7 E9
Рис. 2.9 Строим двумерную таблицу: A b c d e f g k 1. {a,c,e} 1 1 1 2. {a,c,g} 1 1 1 3. {a,k, e} 1 1 1 4. {a,k,d} 1 1 1 5. {a,d,g} 1 1 1 6. {f,d,k} 1 1 1 7. {f,d,b} 1 1 1 8. {f,c} 1 1 9. {b,d,g} 1 1 1 10. {b,e} 1 1
Минимальное число строк, покрывающих все столбцы таблицы, три. Например, строки 1,6,9. Значит h( т.е. H(G)= h( Задачи для самостоятельного решения. 1. Оценить хроматическое число h(G) графа G = < V, U >, у которого V = {1,2,3,4,5,6}, U= {(1,2),(1,6), (2,3), (2,4),(2,6) (3,4),(4,5), (4,6), (5,6)}. 2. Определить хроматическое число графа G, заданного в задаче 1. 3. Найти хроматический класс графа G, заданного в задаче 1. 4. Построить для графа G, заданного в задаче 1, граф 5. Построить граф F5 и проверить на нем т.2.7. ПЛАНАРНОСТЬ ГРАФА. Графы G и Пример 1. Являются ли графы G (рис. 3.1а) и
v3 u4 v4 u3
u3 u5
u5 u5 u5 u5 u4 uu u1 G v4 а) б) Рис. 3.1
Граф G: вершина v1 коинцидентна ребрам u1, u2, u3; вершина v2 коинцидентна ребрам u2, u5, u6; вершина v3 коинцидентна ребрам u3, u4, u6; вершина v4 коинцидентна ребрам u1, u4, u5. Граф вершина v1 коинцидентна ребрам u1, u2, u3; вершина v2 коинцидентна ребрам u2, u5, u6; вершина v3 коинцидентна ребрам u3, u4, u6; вершина v4 коинцидентна ребрам u1, u4, u5.
Отношение коинцидентности выполняется, значит, графы G и изоморфны. ■ Граф называется планарным (плоским), если существует изоморфный ему граф (геометрическая реализация), который может быть изображен на плоскости без пересечения ребер. В рассмотренном примере граф G является планарным, т.к. граф Свойства планарности не нарушится, если некоторое ребро разбить на два ребра введением вершины второй степени или заменить два ребра, инцидентных вершине второй степени, одним ребром, удалив эту вершину. Два графа называются гомеоморфными (изоморфными с точностью до вершины второй степени), если после удаления из них вершин второй степени и объединения инцидентных этим вершинам ребер, они оказываются изоморфными. Граф, гомеоморфный планарному графу, также является планарным. Пример 2. Являются ли граф G (рис. 3.2а) и граф
G v4 а) б) Рис. 3.2
вершин второй степени v5, v6, v7 и объединения инцидентных этим вершинам ребер u3 и u8, u4 и u7, u1 и u9 и после удаления в графе Теорема 3.1 (теорема Л.С. Понтрягина). Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного F5 или К3,3. Граф F5 – минимальный полный граф, который не является планарным (рис. 3.3а). Удаление одного ребра делает этот граф планарным. Граф К3,3 – минимальный полный граф, который не является планарным (рис. 3.3б). Удаление одного ребра делает этот граф планарным. Графы F5 и К3,3 называют часто запрещенными фигурами.
F5 Рис. 3.3 Планарность графов играет существенную роль при проектировании коммуникаций и связи между объектами на плоскости (дороги между населенными пунктами, водопроводные и газопроводные сети, линии электропередач, межсоединения на печатных платах и кристаллах интегральных схем и т.д.). Толщина графа G называется наименьшее число планарных графов, объединение которых дает G. Толщина планарного графа равна 1. Нижняя оценка толщины t(G) графа G = < V, U > определяется неравенством
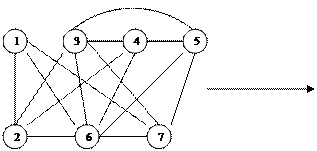
где Отметим, что для строгого доказательства планарности графа используется теорема Понтрягина, соотношение (3.1) лишь только нижняя оценка толщины графа. Пример 3. Является ли граф G (рис. 3.4) планарным? Если нет, то определить, какие ребра необходимо удалить (реализовать на других плоскостях) для преобразования графа G в планарный.
G Рис. 3.4
Проверку можно сделать следующим образом: удаляя минимальное количество вершин и некоторое количество ребер, попытаться привести заданный граф G к виду графа F5. В приведенном графе могут присутствовать вершины второй степени. В графе F5 все вершины имеют степень, равную 4, значит, в графе G можно удалить вершину 1 с инцидентным ей ребрами, т.к. степень вершины 1 равна 3. Дальнейшие преобразования показаны на рис. 3.5.
Рис. 3.5 В результате получили подграф, гомеоморфный F5 , т.е. заданный граф G не является планарным. Удаление любого ребра в полученном подграфе делает его (подграф) планарным. Теперь проверим граф G на содержание подграфа, гомеоморфного К3,3. Попытаемся привести граф G к виду К3,3. В графе К3,3 все вершины имеют степень, равную 3. В графе G степень вершин больше или равна 3, поэтому в процессе преобразования графа G вершины удалять не будем. Сведение графа G к виду графа К3,3 показано на рис. 3.6.
Рис. 3.6 В результате получен подграф, гомеоморфный К3,3. Удаление любого ребра в полученном подграфе делает его планарным.
Вывод: заданный граф G содержит подграфы, гомеоморфные F5 и К3,3, толщина графа G не меньше двух, значит, граф G непланарный. Так как удаление любого ребра выводит запрещенную фигуру (полученные подграфы) из класса подграфов, гомеоморфных F5 и К3,3, то граф G станет планарным; если удалить ребро, входящее как в подграф, гомеоморфный F5 , так и в подграф, гомеоморфный К3,3. Такими общими ребрами являются ребра (2,3), (2,4), (3,6), (4,5),(4,6), (5,7). Удаление любого из этих ребер делает граф планарным. После удаления, например, для определенности ребра (3,6) получаем планарный граф, плоское представление которого изображено на рис. 3.7. Соединение, которое соответствует удаленному ребру (показано пунктирной линией), реализуется на второй плоскости. Толщина t(G) графа G равна 2. ■
G Рис.3.7
Задачи для самостоятельного решения. 1.
G1 G2 G3 Рис. 3.8 2. Покажите, что графы, изображенные на рис. 3.9., гомеоморфные.
Рис. 3.9 3. Покажите, что приведенные на рис. 3.9 графы непланарные. Какое минимальное число ребер необходимо удалить, чтобы они стали планарными. 4. Найти нижнюю оценку толщины графов, изображенных на рис. 3.9. 5. Задача о трех домах и трех колодцах: можно ли продолжить от домов к каждому колодцу дороги так, чтобы они не пересекались (враждующие соседи должны иметь возможность пользоваться всеми колодцами, но не хотят встречаться на дороге)?
СПИСОК ЛИТЕРАТУРЫ 1. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. – 311 с. 2. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1986 – 480с. 3. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987 – 496с. 4. Сигорский В.П. Математический аппарат инженера. – Киев: Технiка, 1975. – 768 с.
СОДЕРЖАНИЕ. 1. Устойчивость, покрытия, паросочетания……………………………. 1.1. Основные определения……………………………………………... 1.2. Определение чисел ε0(G), π0(G), π1(G)…………………………….. 1.3. Определение чисел β0(G), β1(G)…………………………………….. 1.4. Определение чисел β0+(G), β0-(G)…………………………………… 1.5. Плотность p(G) графа G……………………………………………… 1.6. Максимальный поток через сеть……………………………………. 2. Раскраска вершин и ребер графа……………………………………… 2.1. Понятие раскраски вершин и ребер графа…………………………. 2.2. Раскраска вершин графа…………………………………………… 2.3. Раскраска ребер графа………………………………………………. 2.4. Алгоритм минимальной раскраски вершин ребер (графа)……….. 3. Планарность графа……………………………………………………… Список литературы…………………………………………………………
Учебное издание
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.237 (0.229 с.) |
 Для определения h(G) необходимо выделить все вершинно пустые подграфы заданного графа G (рис. 2.4).
Для определения h(G) необходимо выделить все вершинно пустые подграфы заданного графа G (рис. 2.4).






 b
b

 c 6 4 b
c 6 4 b Выделяем реберно пустые подграфы заданного графа G, предварительно обозначив ребра буквами (рис. 2.7)
Выделяем реберно пустые подграфы заданного графа G, предварительно обозначив ребра буквами (рис. 2.7) 2
2




 f g c
f g c
 4
4


 b
b















 e
e




 d
d


































 f g c
f g c
 ) графа
) графа 









 b g
b g






 g g
g g











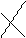



 ,
,  > и показать, что H(G)= h(
> и показать, что H(G)= h(






 v3 v1
v3 v1
 v1 u2 v2
v1 u2 v2 Проверим, например, для этих графов сохранение отношения коинцидентности.
Проверим, например, для этих графов сохранение отношения коинцидентности.




 u2 u9 u8 u3
u2 u9 u8 u3




 Графы G и
Графы G и 











 К3,3
К3,3
 1 +
1 +  , (3.1)
, (3.1) - ближайшее целое число, n=|v|, Si - степень i–ой вершины.
- ближайшее целое число, n=|v|, Si - степень i–ой вершины.









 =2, т.е. t(G)
=2, т.е. t(G) 








 Изоморфны ли графы, изображенные на рис. 3.8?
Изоморфны ли графы, изображенные на рис. 3.8?
















