
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический способ решения ЗЛП
Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.
1. С учетом системы ограничений строим область допустимых решений 2. Строим вектор
3. Проводим произвольную линию уровня 4. При решении задачи на максимум перемещаем линию уровня 5. Определяем оптимальный план
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит: 1) умение находить начальный опорный план; 2) наличие признака оптимальности опорного плана; Пусть ЗЛП представлена системой ограничений в каноническом виде:
Которая имеет предпочтительный вид
причём ни одно из ограничений не имеет предпочтительной переменной. М-задача запишется так:
Задача о смесях(о диете) К задачам о диете относятся задачи, в которых требуется выбрать самый дешевый пищевой рацион, содержащий необходимое количество указанных заранее питательных веществ. Предполагается, что: 1. Известен перечень биологически необходимых питательных веществ и их минимальная норма (например, суточная); 2. Задан набор продуктов, из которых требуется составить пищевой рацион; 3. Имеются нормы содержания различных питательных веществ в единице соответствующего продукта; 4. Известна цена единицы каждого продукта, который может быть использован в пищевом рационе. Подобная проблема возникает при выборе рационального корма для скота. Формализуем описанную ситуацию: Будем считать, что в рацион должно входить m биологически необходимых питательных веществ (индекс i). Таким образом, i=1,2,..,m. Известно, что i -го питательного вещества в рационе должно быть не меньше, чем bi единиц. Предположим, что мы располагаем n различными продуктами, из которых составляется пищевой рацион (индекс j, j=1,2,…,n). Норму содержания i -го питательного вещества в j -ом продукте обозначим через aij. Нам известна таблица-матрица, состоящая из m×n чисел aij . Таблица 2.1
Цены, которые установлены на продукты питания, обозначим cj за единицу j -го продукта. Количество j -го продукта, входящего в пищевой рацион, обозначим через xj. В этих обозначениях выбор самого дешевого рациона, удовлетворяющего сформулированным выше требованиям, сводится к решению следующей математической задачи: Найти вектор X = (x1, x2, …, xn), удовлетворяющий системе ограничений:
и доставляющий целевой функции Ограничение для каждого i означает, что в выбираемом рационе i -го питательного вещества должно содержать не менее, чем bi единиц. Второе ограничение формализует тот факт, что j -ый продукт может либо входить в рацион, и тогда xi >0, либо не входить, и тогда xi =0.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.70.101 (0.023 с.) |
 (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13)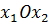 некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (2.11) — (2.13) есть выпуклое множество.
некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (2.11) — (2.13) есть выпуклое множество. .
.
 . Получим
. Получим  . Это уравнение прямой линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение
. Это уравнение прямой линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение  . Считая в равенстве (2.11) F параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
. Считая в равенстве (2.11) F параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения). и
и  :
: (2.14)
(2.14) . (2.15)
. (2.15) и
и  — скорости возрастания F соответственно вдоль осей
— скорости возрастания F соответственно вдоль осей  и
и  .Вектор
.Вектор  =(
=( называется градиентом функции.Он показывает направление наискорейшего возрастания целевой функции:
называется градиентом функции.Он показывает направление наискорейшего возрастания целевой функции:
 (2.16)
(2.16) указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом. семейства
семейства  .
. =(
=( .
. в направлении вектора
в направлении вектора 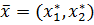 и экстремальное значение целевой функции
и экстремальное значение целевой функции  .
.
 ,
,  .
. ,
,  (
(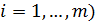 . Получим систему, эквивалентную исходной:
. Получим систему, эквивалентную исходной: ,
, ).
). .
.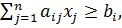
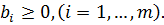
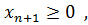 (
( систему
систему .
. входят в левую часть (при
входят в левую часть (при  ) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план
) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план  ) не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные
) не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные  . В целевую функцию переменные
. В целевую функцию переменные  )
)  , (2.17)
, (2.17) (2.18)
(2.18) , (2.19)
, (2.19) (2.20)
(2.20) (
( (2.22)
(2.22) ) (2.23)
) (2.23)
 , то план
, то план  является оптимальным планом исходной задачи(2.17)-(2.19).
является оптимальным планом исходной задачи(2.17)-(2.19). называется симплексным методом с искусственным базисом.
называется симплексным методом с искусственным базисом. , то его первые n-компоненты дают оптимальный план исходной задачи.
, то его первые n-компоненты дают оптимальный план исходной задачи.



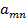
 (
( минимальное значение.
минимальное значение.


