
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула включений и исключений
ï A È B ï = ï A ï + ï B ï – ï A Ç B ï
5. Декартово произведение множеств. Соответствие. Пустое соответствие, полное соответствие. Область определения, прообраз (Dom) соответствия. Область значений, образ (Im) соответствия. Всюду определенные и сюръективные соответствия. Образ (im) и прообраз (coim) элемента. Соответствие как частично определенная многозначная функция.
Соответствием между множествами А и В называется некоторое подмножество R их декартова произведения: Пусть R Í A ´ B. Областью определения Dom R называется множество элементов a Î A, для каждого из которых найдется хотя бы один элемент b Î B такой, что aRb. Областью значений, или образом, Im R соответствия R называется множество элементов b Î B, для каждого из которых найдется хотя бы один элемент a Î A такой, что aRb. Соответствие R называется всюду определенным, если Dom R = A, и сюръективным, если Im R = B. Для каждого a Î A множество элементов b Î B таких, что aRb, называется образом a относительно R и обозначается im R a. Прообразом элемента b Î B относительно R называется множество элементов a Î A таких, что aRb; прообраз обозначается coim R b. Каждое соответствие однозначно определяет функцию a ® im R a, которая отображает множество A в множество подмножеств B. Обратно, всякая функция f из множества A в множество подмножеств B определяет некоторое соответствие R (f): aR (f) b тогда и только тогда, когда b Î f (a). Указанные сопоставления взаимно однозначны, что позволяет рассматривать соответствия как частично определенные многозначные функции.
6. Способы задания соответствий. Инволюция (обращение) соответствий. Объединение, пересечение, дополнение, произведение соответствий. Соответствием между множествами А и В называется некоторое подмножество R их декартова произведения:
A = { a, b, c }, B = { x, y }, R = {(a, x), (a, y), (b, y), (c, x)}. Каждая матрица подобного вида однозначно определяет соответствие между A и B.
Инволюция (обращение соответствия): если R Í A x B, то инволюция R # состоит из таких пар (b, a), что (a, b) Î R. Иногда вместо R # пишут R -1. Ясно, что R ## = R. Для бинарных отношений обычным образом определены теоретико-множественные операции объединения, пересечения и т.д. Дополнение соответствия:
7. Функциональные соответствия, их связь с графиками функций. Соответствие Пример 1. а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка. Оно не является функциональным, так как почти каждому русскому слову соответствует несколько английских переводов; оно, также, не является, как правило, полностью определённым соответствием, так как всегда существуют английские слова, не включённые в данный словарь. Таким образом, это частичное соответствие. б) Соответствие между аргументами функции
8. Соответствие Галуа и его роль в проективном распознавании образов. Замкнутое подмножество. Соответствием между множествами А и В называется некоторое подмножество R их декартова произведения: · Именно, если X Í A, то через G (X) обозначается пересечение Ç a Î Xim R a; · Аналогично, для Y Í B вводится множество G^–1(Y)= Ç b Î Y coim R b. · Пусть X * = G^–1 (G (X)), Y * = G(G^–1(Y)), тогда X Í X *, Y Í Y *; Подмножество X Í A (Y Í B) называется замкнутым, если X = X * (Y = Y *). Соответствие Галуа устанавливает биективное соответствие между замкнутыми подмножествами в A и B.
9. Отношение. Бинарные отношения и способы их задания. Операции над бинарными отношениями. Обратные отношения. Композиция бинарных отношений. Отношение -произвольное подмножество R множества An всех кортежей (упорядоченных наборов) вида (a1,..., an), где a1,..., an -элементы некоторого множества A; в этом случае говорят, что R есть n -мерное отношение на A. Двухмерные отношения называются бинарными. Если R - бинарное отношение, то вместо (a, b) Î R, часто пишут aRb. Пример. Бинарные отношения на множестве точек координатной плоскости. Частным случаем понятия отношения является соответствие.
A = { a, b, c }, B = { x, y }, R = {(a, x), (a, y), (b, y), (c, x)}. Тогда R сопоставляется матрица: Каждая матрица подобного вида однозначно определяет соответствие между A и B. При графовом представлении элементы множеств A и B изображаются точками на плоскости. Обычно эти точки обозначаются теми же символами, что и соответствующие элементы. Точки a и b соединяются направленной дугой от a к b, если aRb. Пусть R Í A ´ A. Соответствие R называется: · рефлексивным, если для · антирефлексивным (для · симметричным, если · антисимметричным, если · асимметричным, если R Ç R # = Æ; · транзитивным, если Отношение R называется: a) эквивалентностью, если оно рефлексивно, симметрично и транзитивно b) толерантностью, если оно рефлексивно и симметрично; c) предпорядком, если оно рефлексивно и транзитивно; d) порядком, если оно транзитивно и антисимметрично.
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.159.224 (0.01 с.) |
 - декартово произведение (множество всех упорядоченных пар)
- декартово произведение (множество всех упорядоченных пар)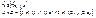
 . Если a Î A, b Î B и (a, b) Î R, то пишут также R (a, b) или aRb. Если R = Æ — пустое множество, то соответствие называется пустым, а если R = A ´ B, то соответствие называется полным.
. Если a Î A, b Î B и (a, b) Î R, то пишут также R (a, b) или aRb. Если R = Æ — пустое множество, то соответствие называется пустым, а если R = A ´ B, то соответствие называется полным. При графовом представлении элементы множеств A и B изображаются точками на плоскости. Обычно эти точки обозначаются теми же символами, что и соответствующие элементы. Точки a и b соединяются направленной дугой от a к b, если aRb.
При графовом представлении элементы множеств A и B изображаются точками на плоскости. Обычно эти точки обозначаются теми же символами, что и соответствующие элементы. Точки a и b соединяются направленной дугой от a к b, если aRb. Произведение: Если R Í A x B, S Í B x C, то произведение
Произведение: Если R Í A x B, S Í B x C, то произведение 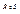 состоит из таких пар (a, c), для которых найдется элемент b Î B такой, что (a, b) Î R, (b, c) Î S.
состоит из таких пар (a, c), для которых найдется элемент b Î B такой, что (a, b) Î R, (b, c) Î S. называется функциональным (однозначным), если любому элементу множества
называется функциональным (однозначным), если любому элементу множества  соответствует единственный элемент множества
соответствует единственный элемент множества  . Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества
. Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества  и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции
и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции  соответствуют два прообраза
соответствуют два прообраза  и
и  . в) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным.
. в) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным. Пусть A = { a 1, a 2,..., an }, B = { b 1, b 2,..., bm } и R Í A ╢ B. Соответствию R сопоставляется матрица размера n ╢ m, строки которой помечены элементами из A, столбцы - элементами из B, а на пересечении строки ai и столбца bj стоит 1, если ai R bj , и 0 в противном случае. Например,
Пусть A = { a 1, a 2,..., an }, B = { b 1, b 2,..., bm } и R Í A ╢ B. Соответствию R сопоставляется матрица размера n ╢ m, строки которой помечены элементами из A, столбцы - элементами из B, а на пересечении строки ai и столбца bj стоит 1, если ai R bj , и 0 в противном случае. Например,
 )
)





