
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим основные геометрические характеристики профиля.Стр 1 из 9Следующая ⇒
Линеаризованная теория тонкого профиля В докритическом потоке
Рассмотрим обтекание тонкого профиля при малом угле атаки. Течение сжимаемого газа около такого профиля можно исследовать с помощью дифференциального уравнения (5.8), линеаризованного методом малых возмущений:
Это уравнение во всей области течения будет эллиптического типа. К этому же типу относится и уравнение Лапласа (для несжимаемой жидкости). Уравнение (5.8) отличается от уравнения Лапласа только множителем при первом члене, поэтому вполне правомерен вопрос о возможности сведения задачи об обтекании профиля потоком сжимаемой жидкости к задаче обтекания некоторого профиля другой формы потоком несжимаемой жидкости. Приведем уравнение (5.8) к виду уравнения Лапласа. Произведем замену переменных Тогда
т. е.
После подстановки исходное дифференциальное уравнение сводится к уравнению Уравнению Лапласа удовлетворяет потенциал скорости потока несжимаемой жидкости. Определив потенциал скорости потока несжимаемой жидкости, через замену переменных При переходе от переменных
 Рассмотрим изменение скоростей в системе координат Рассмотрим изменение скоростей в системе координат  в направлении координатных осей. Так как в направлении координатных осей. Так как  и и  , то , то  и и  . То есть составляющая скорости по оси X не изменяется, а по оси Y увеличивается в отношении . То есть составляющая скорости по оси X не изменяется, а по оси Y увеличивается в отношении  . Это означает увеличение углов наклона касательной к линии тока с осью X, величину которых можно оценить через отношение . Это означает увеличение углов наклона касательной к линии тока с осью X, величину которых можно оценить через отношение  . Следовательно, в этом же отношении увеличивается и угол атаки . Следовательно, в этом же отношении увеличивается и угол атаки  , т. е. , т. е.  . .
Это же говорит и о том, что исходный контур утолщается, а максимальная толщина профиля
Таким образом, можно считать, что тонкому профилю в сжимаемой среде соответствует утолщенный профиль в несжимаемой жидкости, обтекаемый под большим углом атаки.
Увеличение угла атаки с одновременным утолщением профиля приводит к увеличению коэффициента подъемной силы профиля
по аналогии, Коэффициент
Волновое сопротивление
Рассмотрим обтекание профиля при числах Маха Физическая природа волнового сопротивления. Рассмотрим схему обтекания профиля закритическим потоком (рис. 8.8). На верхней поверхности симметричного профиля при нулевом угле атаки приведена схема течения, а на нижней – соответствующая ей эпюра давления.
Если бы в рассмотренном диапазоне скоростей было возможно только изоэнтропическое обтекание (без скачков), то давление в кормовой части профиля было бы выше и равно
Волновое сопротивление тем больше, чем больше потери полного давления в скачке. Величина коэффициента волнового сопротивления зависит от числа Маха Приближенный метод определения волнового сопротивления. Рассмотрим профиль со скачком на верхней поверхности (рис. 8.9). Выделим элементарную струйку, проходящую через скачок уплотнения. Проведем на расстоянии, достаточно удаленном от профиля, две контрольные поверхности I–I и II–II.
Из условия постоянства расхода следует:
где
Во всех струйках, не пересекающих скачок уплотнения, После некоторых преобразований можно получить выражение для коэффициента волнового сопротивления профиля:
где А – постоянный коэффициент, который в общем случае зависит от формы профиля (для большинства современных профилей А Формулой (8.2) можно пользоваться до
Особенности обтекания крыла конечного размаха дозвуковым потоком
Аэродинамические характеристики крыла конечного размаха зависят как от формы сечения (профиля), так и от формы крыла в плане.
Циркуляцию скорости Г присоединенного вихря в данной задаче определим исходя из условия равенства подъемной силы крыла силе, создаваемой П-образным вихрем:
где Каждый свободный концевой вихрь индуцирует вокруг себя поле скоростей. Профили скорости
Средняя по размаху крыла скорость
Подставив значение циркуляции из уравнения (8.3), учтем, что
Скорость Ввиду малости угла скоса,
Допустим, что крыло установлено под углом Создаваемая крылом подъемная сила Ввиду малости
Формула (8.8) показывает, что индуктивное сопротивление обязано своим появлением подъемной силе – главной цели создания крыльев – и конечности размаха крыла. Индуктивное сопротивление и коэффициент индуктивного сопротивления равны нулю при нулевой подъемной силе (
Линеаризованная теория обтекания плоской пластинки сверхзвуковым потоком
Рассмотренная ранее схема линеаризации течений разрежения и уплотнения (см. гл. 5) позволяет просто решить задачу обтекания плоской пластинки при малых углах атаки a.
Линия тока, направленная вдоль верхней поверхности, испытывает в носовой части возмущение в виде разрежения Так как между передней и задней кромками обеих поверхностей нет источников возмущения, то скорости потока и давления на этих поверхностях постоянны и равны
и
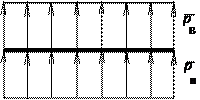
В дозвуковом потоке 75 % подъемной силы создается за счет разрежения на верхней поверхности, и только 25 % – за счет повышенного давления на нижней. В сверхзвуковом потоке (рис. 8.13), в отличие от дозвукового, как следует из формул (8.9), (8.9а) давление вдоль верхней и нижней поверхностей пластинки распределяется равномерно (рис. 8.13, а), а центр давления располагается посредине пластины:
а б
Рис. 8.13. Распределение давления и коэффициента давления по верхней и нижней сторонам пластинки: а – давления; б – коэффициента давления
Найдем нормальную силу, которая действует на пластину:
При малых углах атаки
Следует помнить, что в этих формулах угол При малых углах атаки (см. рис. 8.2, зависимости
Как следует из формул (8.10), (8.10а) с ростом числа Момент аэродинамической силы относительно передней кромки равен
ведет себя таким же образом, как и другие аэродинамические коэффициенты: при увеличении числа
В сверхзвуковом потоке
Рассмотрим обтекание тонкого слабоизогнутого крыла конечного размаха произвольной формы в плане установившимся сверхзвуковым потоком невязкого газа. Будем считать, что создаваемые крылом возмущения малы. Тогда можно применить правило наложения потоков и записать потенциал скорости как
Рассмотрим граничные условия, которым должен удовлетворять
1) внутри волновой поверхности 2) вне ее То есть граничное условие на поверхности При наличии подъемной силы ( На вихревой пелене скорость (
На основе линеаризованного уравнения Бернулли (5.7) можно сделать вывод, что при Так как потенциал скорости возмущения удовлетворяет линейному дифференциальному уравнению (8.11), поток в окрестности тонкого крыла произвольной формы можно получить в результате наложения потока около крыла нулевой толщины при заданном Зная
где Коэффициент сопротивления крыла равен сумме коэффициентов сопротивления
Для профиля и крыла
Рассмотрим некоторые инженерные зависимости, позволяющие провести оценочный расчет аэродинамических характеристик профиля и крыла конечного размаха при дозвуковых и сверхзвуковых скоростях.
Рассчитаем лобовое сопротивление. В диапазоне дозвуковых скоростей главной составляющей силы лобового сопротивления является сопротивление трения. Более того, сопротивление трения есть при любых скоростях движения. На его величину кроме скорости движения влияют форма профиля и состояние пограничного слоя. Малые дозвуковые скорости ( При ламинарном пограничном слое коэффициент сопротивления трения для профиля определяется как для пластины в несжимаемой жидкости, например, по формуле Блазиуса:
С увеличением скорости потока коэффициент сопротивления трения уменьшается вследствие уменьшения толщины пограничного слоя. При турбулентном пограничном слое на профиле также используют зависимости, полученные для плоской пластинки и несжимаемой жидкости. Причем в зависимости от величины числа Рейнольдса применяют расчетные формулы разного вида. Так в диапазоне
а при
Докритические скорости (
Закритические скорости (
а) уменьшения относительной толщины профиля б) заострения носа профиля при одинаковых относительных толщинах Меньшее сопротивление тупоносых профилей 2 (рис. 8.21) при дозвуковых и трансзвуковых скоростях объясняется возникновением подсасывающей силы, уменьшающей общее сопротивление за счет большого разрежения у передней кромки профиля. Сверхзвуковые скорости. Для сверхзвуковых скоростей полета оптимальной формой профиля является ромб с несколько смещенной назад максимальной толщиной. Имея ввиду малость возмущений, вносимых тонким профилем в сверхзвуковой поток, коэффициент волнового сопротивления можно представить в виде суммы двух составляющих: Тогда формула для расчета
где K – коэффициент формы профиля, значения которого приведены в табл. 8.1.
Таблица 8.1 Рассмотрим основные геометрические характеристики профиля. Хорда – отрезок прямой, соединяющий две наиболее удаленные точки профиля А и В; длина хорды обычно обозначается буквой b. Контур профиля принято задавать относительными координатами верхнего Средняя линия – геометрическое место точек, равноотстоящих от верхнего и нижнего обводов по перпендикуляру к хорде. Координаты средней линии можно найти по формуле Расстояние между верхней и нижней частями контура в каком-нибудь сечении, перпендикулярном хорде, называется абсолютной толщиной профиля (изменяется вдоль хорды) и обозначается с. Максимальную толщину обычный тонкий дозвуковой профиль имеет в сечении Относительная толщина профиля – отношение максимальной толщины к длине хорды Относительная вогнутость – отношение максимальной ординаты средней линии (стрелы прогиба) к длине хорды: Аэродинамические характеристики профилей обычно представляют с помощью коэффициентов сил и моментов:
В аэродинамической практике часто используют такое понятие, как качество профиля Аэродинамические характеристики различных профилей помещены в атласах профилей в виде таблиц или (и) графических зависимостей. На графиках (рис. 8.2) приведены примерные зависимости коэффициентов подъемной силы и силы лобового сопротивления для несимметричного профиля от угла атаки (рис. 8.2, а) и так называемая поляра первого рода – зависимость
а б Рис. 8.2. Аэродинамические характеристики профиля: а – несимметричный профиль; б – поляра первого рода
Остановимся более подробно на зависимостях При больших углах атаки линейность изменения Поляра первого рода дает возможность получить данные о коэффициентах
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.156.140 (0.167 с.) |
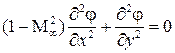 .
.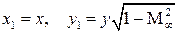 .
.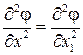 ,
,  ,
,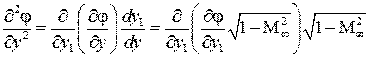 ,
, .
.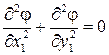 , которое и является уравнением Лапласа.
, которое и является уравнением Лапласа. и
и  получим скорость потока сжимаемой жидкости.
получим скорость потока сжимаемой жидкости.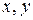 к
к  изменяется форма профиля. Допустим, что в плоскости XОY расположен тонкий профиль с хордой
изменяется форма профиля. Допустим, что в плоскости XОY расположен тонкий профиль с хордой  , направленной вдоль оси Х. Профиль обтекает под малым углом атаки
, направленной вдоль оси Х. Профиль обтекает под малым углом атаки  потоком сжимаемой среды со скоростью
потоком сжимаемой среды со скоростью  (рис. 8.7). В таком случае в плоскости
(рис. 8.7). В таком случае в плоскости 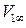 при угле атаки
при угле атаки  в несжимаемой среде становится равной
в несжимаемой среде становится равной .
. . Следовательно, при известном значении коэффициента подъемной силы профиля в несжимаемом газе
. Следовательно, при известном значении коэффициента подъемной силы профиля в несжимаемом газе  , коэффициент подъемной силы профиля в сжимаемом газе
, коэффициент подъемной силы профиля в сжимаемом газе  для данного угла атаки при малых скоростях обтекания находится как
для данного угла атаки при малых скоростях обтекания находится как (8.1)
(8.1) и коэффициент момента
и коэффициент момента  .
. называют поправкой на сжимаемость Прандтля–Глауэрта, а рассмотренный метод учета влияния сжимаемости на аэродинамические характеристики профиля – методом Прандтля–Глауэрта.
называют поправкой на сжимаемость Прандтля–Глауэрта, а рассмотренный метод учета влияния сжимаемости на аэродинамические характеристики профиля – методом Прандтля–Глауэрта. . В этом диапазоне чисел
. В этом диапазоне чисел  возникают зоны местных сверхзвуковых скоростей, замыкающиеся скачками уплотнения, необратимые потери механической энергии в которых вызывают дополнительное волновое сопротивление.
возникают зоны местных сверхзвуковых скоростей, замыкающиеся скачками уплотнения, необратимые потери механической энергии в которых вызывают дополнительное волновое сопротивление. В передней критической точке скорость течения
В передней критической точке скорость течения  , а давление
, а давление  . При удалении от передней критической точки давление уменьшается, а скорость течения увеличивается. В точке А профиля
. При удалении от передней критической точки давление уменьшается, а скорость течения увеличивается. В точке А профиля 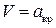 и
и  . Далее вниз по потоку скорость течения становится сверхзвуковой и продолжает расти, а давление уменьшается. Непосредственно перед скачком
. Далее вниз по потоку скорость течения становится сверхзвуковой и продолжает расти, а давление уменьшается. Непосредственно перед скачком  и
и  . За скачком уплотнения скорость течения становится дозвуковой, давление
. За скачком уплотнения скорость течения становится дозвуковой, давление  , и при приближении к задней кромке скорость течения продолжает изоэнтропически уменьшаться до нуля, а давление возрастает до давления заторможенного за скачком уплотнения потока.
, и при приближении к задней кромке скорость течения продолжает изоэнтропически уменьшаться до нуля, а давление возрастает до давления заторможенного за скачком уплотнения потока. . Скачок уплотнения приводит к понижению давления в кормовой части, что и обусловливает появление дополнительного, так называемого волнового, сопротивления.
. Скачок уплотнения приводит к понижению давления в кормовой части, что и обусловливает появление дополнительного, так называемого волнового, сопротивления. перед скачком уплотнения. Чем больше
перед скачком уплотнения. Чем больше 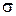 , т. е. больше потери и больше коэффициент волнового сопротивления.
, т. е. больше потери и больше коэффициент волнового сопротивления. Параметры течения на поверхности I–I –
Параметры течения на поверхности I–I –  , а на II–II –
, а на II–II –  .
. =
=  , где dy – элемент длины вдоль контрольной поверхности. Применяя теорему о количестве движения к массе газа, заключенной между контрольными поверхностями, получаем следующее:
, где dy – элемент длины вдоль контрольной поверхности. Применяя теорему о количестве движения к массе газа, заключенной между контрольными поверхностями, получаем следующее: ,
, – волновое сопротивление. С учетом уравнения неразрывности
– волновое сопротивление. С учетом уравнения неразрывности  и принимая во внимание, что
и принимая во внимание, что  , выражение для
, выражение для 
 и
и  . Тогда для определения величины силы сопротивления интегрирование можно производить только по длине скачка. Считая
. Тогда для определения величины силы сопротивления интегрирование можно производить только по длине скачка. Считая  . Но так как
. Но так как 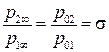 , а также учитывая, что
, а также учитывая, что  и
и  , получаем
, получаем  . Поскольку
. Поскольку  , то
, то  , и при уменьшении величины коэффициента восстановления полного давления (с увеличением числа Маха и интенсивности скачка) сила волнового сопротивления возрастает.
, и при уменьшении величины коэффициента восстановления полного давления (с увеличением числа Маха и интенсивности скачка) сила волнового сопротивления возрастает. (8.2)
(8.2) ).
). . Из нее следует, что при заданном
. Из нее следует, что при заданном 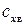 возможно путем увеличения
возможно путем увеличения  .
. Рассмотрим крыло конечного размаха. Заметим, что характеристики сечений крыла различны из-за влияния перетекания воздуха через боковые кромки крыла. Профиль, а значит и крыло, создает подъемную силу только тогда, когда циркуляция вектора скорости вокруг профиля
Рассмотрим крыло конечного размаха. Заметим, что характеристики сечений крыла различны из-за влияния перетекания воздуха через боковые кромки крыла. Профиль, а значит и крыло, создает подъемную силу только тогда, когда циркуляция вектора скорости вокруг профиля  . То есть, по своему действию можно заменить систему профилей, составляющих крыло, присоединенным вихрем. Заменим крыло простейшей вихревой системой – одним П-об-разным присоединенным вихрем (рис. 8.10).
. То есть, по своему действию можно заменить систему профилей, составляющих крыло, присоединенным вихрем. Заменим крыло простейшей вихревой системой – одним П-об-разным присоединенным вихрем (рис. 8.10). , т. е.
, т. е. , (8.3)
, (8.3) – расстояние между свободными полубесконечными вихрями, сбегающими с концов крыла. Это расстояние больше размаха крыла на некоторую величину:
– расстояние между свободными полубесконечными вихрями, сбегающими с концов крыла. Это расстояние больше размаха крыла на некоторую величину:  . Можно принять, что
. Можно принять, что  .
. для левого и правого концевых вихрей, а также эпюра суммарной скорости приведены на рис. 8.10. При начале координат в центре крыла величина скорости, индуцируемой обоими вихрями и направленной вниз, может быть определена по формуле Био–Савара для полубесконечного вихря
для левого и правого концевых вихрей, а также эпюра суммарной скорости приведены на рис. 8.10. При начале координат в центре крыла величина скорости, индуцируемой обоими вихрями и направленной вниз, может быть определена по формуле Био–Савара для полубесконечного вихря  как
как . (8.4)
. (8.4) или с учетом выражения (8.4) после интегрирования получим
или с учетом выражения (8.4) после интегрирования получим . (8.5)
. (8.5) , и проведем замену
, и проведем замену  (удлинение крыла). Тогда при
(удлинение крыла). Тогда при  получим
получим  , и из формулы (8.5) следует, что
, и из формулы (8.5) следует, что . (8.6)
. (8.6) Анализ формулы (8.6) показывает, что за появление индуцированной скорости ответственны подъемная сила и конечность крыла (для реального крыла
Анализ формулы (8.6) показывает, что за появление индуцированной скорости ответственны подъемная сила и конечность крыла (для реального крыла  ). Индуктивная скорость изменяет действительный угол атаки крыла (рис. 8.11), поскольку вблизи поверхности крыла скорость течения
). Индуктивная скорость изменяет действительный угол атаки крыла (рис. 8.11), поскольку вблизи поверхности крыла скорость течения  .
. отклоняется от вектора скорости набегающего потока
отклоняется от вектора скорости набегающего потока  на угол скоса
на угол скоса  .
. . С учетом формулы (8.6)
. С учетом формулы (8.6) . (8.7)
. (8.7) . Чем больше удлинение крыла
. Чем больше удлинение крыла 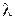 , тем меньше скос потока и меньше различие между истинным и установочным углами атаки.
, тем меньше скос потока и меньше различие между истинным и установочным углами атаки. , перпендикулярная вектору местной скорости
, перпендикулярная вектору местной скорости  , дает составляющую
, дает составляющую  на направление скорости набегающего потока. Поскольку появление этой составляющей спровоцировано скосом потока за счет индуцированных концевыми вихрями скоростей, то ее принято называть силой индуктивного сопротивления. В соответствии с рис. 8.11 можно записать выражения для коэффициентов подъемной силы и индуктивного сопротивления:
на направление скорости набегающего потока. Поскольку появление этой составляющей спровоцировано скосом потока за счет индуцированных концевыми вихрями скоростей, то ее принято называть силой индуктивного сопротивления. В соответствии с рис. 8.11 можно записать выражения для коэффициентов подъемной силы и индуктивного сопротивления:  .
. и
и 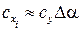 . С учетом выражения (8.7) для угла скоса потока, получим
. С учетом выражения (8.7) для угла скоса потока, получим . (8.8)
. (8.8)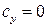 ) или при
) или при  .
. Рассмотрим обтекание плоской пластинки, расположенной под малым углом атаки к вектору скорости
Рассмотрим обтекание плоской пластинки, расположенной под малым углом атаки к вектору скорости  , а в кормовой части – в виде сжатия
, а в кормовой части – в виде сжатия  . Для нижней поверхности порядок следования возмущений противоположный
. Для нижней поверхности порядок следования возмущений противоположный  .
.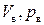 и
и  . Для нахождения давлений и коэффициентов давлений воспользуемся полученными ранее формулами (5.10) и (5.10а) для линеаризованного течения, подставляя в них
. Для нахождения давлений и коэффициентов давлений воспользуемся полученными ранее формулами (5.10) и (5.10а) для линеаризованного течения, подставляя в них 
 и учитывая, что для верхней поверхности
и учитывая, что для верхней поверхности  , а для нижней
, а для нижней  . Тогда
. Тогда ,
,  , (8.9)
, (8.9) ,
,  . (8.9а)
. (8.9а) . В дозвуковом потоке
. В дозвуковом потоке 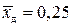 . Так как коэффициенты давления
. Так как коэффициенты давления  (рис. 8.13, б), то по линейной теории в сверхзвуковом потоке подъемная сила создается в одинаковой мере верхней и нижней поверхностями.
(рис. 8.13, б), то по линейной теории в сверхзвуковом потоке подъемная сила создается в одинаковой мере верхней и нижней поверхностями.
 .
. Тогда подъемная сила равна
Тогда подъемная сила равна 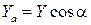 (рис. 8.14), а волновое сопротивление
(рис. 8.14), а волновое сопротивление  (другие виды сопротивления отсутствуют, так как жидкость идеальная, а пластинка имеет бесконечный размах).
(другие виды сопротивления отсутствуют, так как жидкость идеальная, а пластинка имеет бесконечный размах). и
и  . Отсюда коэффициенты сил
. Отсюда коэффициенты сил  и
и  . С учетом выражений (8.9а) для коэффициентов давлений получаем
. С учетом выражений (8.9а) для коэффициентов давлений получаем ,
,  . (8.10)
. (8.10) от
от  , т. е. для плоской пластинки
, т. е. для плоской пластинки . (8.10а)
. (8.10а)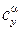 уменьшаются.
уменьшаются. (положительным считается момент на кабрирование, т. е. на увеличение
(положительным считается момент на кабрирование, т. е. на увеличение 
 , где
, где  – потенциал скорости невозмущенного потока;
– потенциал скорости невозмущенного потока;  – потенциал скорости возмущений. Функции
– потенциал скорости возмущений. Функции 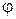 и
и  (8.11)
(8.11) Крыло вызывает возмущения внутри волновой поверхности
Крыло вызывает возмущения внутри волновой поверхности  , огибающей конусы возмущений (рис. 8.20). Волновая поверхность разбивает всю область потока на две части:
, огибающей конусы возмущений (рис. 8.20). Волновая поверхность разбивает всю область потока на две части: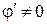 ;
;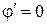 .
. . Согласно условию непротекания на поверхности крыла
. Согласно условию непротекания на поверхности крыла  .
. ) за крылом образуется вихревая пелена. Для тонкого крыла при малом
) за крылом образуется вихревая пелена. Для тонкого крыла при малом  ) и давление непрерывны, т. е. при приближении к вихревой пелене сверху (
) и давление непрерывны, т. е. при приближении к вихревой пелене сверху ( ) или снизу (
) или снизу ( )
) ,
,  .
. скорость
скорость  , т. е.
, т. е. 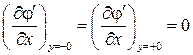 .
. и потока около крыла с симметричным профилем –
и потока около крыла с симметричным профилем –  при
при  .
. можно определить скорость в каждой точке потока, в том числе и на поверхности крыла, а также найти распределение давления
можно определить скорость в каждой точке потока, в том числе и на поверхности крыла, а также найти распределение давления 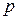 и коэффициента давления
и коэффициента давления  как
как ,
, – коэффициент давления для крыла нулевой толщины при несимметричном обтекании (
– коэффициент давления для крыла нулевой толщины при несимметричном обтекании ( );
);  – коэффициент давления для крыла с симметричным профилем конечной (малой) толщины при
– коэффициент давления для крыла с симметричным профилем конечной (малой) толщины при  не создает подъемной силы). Поэтому для определения
не создает подъемной силы). Поэтому для определения  тонкого крыла достаточно решить задачу обтекания крыла нулевой толщины (пластинки) при заданном угле атаки.
тонкого крыла достаточно решить задачу обтекания крыла нулевой толщины (пластинки) при заданном угле атаки. при нулевом угле атаки и
при нулевом угле атаки и  , обусловленного подъемной силой (индуктивно-волновое сопротивление):
, обусловленного подъемной силой (индуктивно-волновое сопротивление): .
. ). В этом диапазоне скоростей газ можно считать несжимаемой жидкостью.
). В этом диапазоне скоростей газ можно считать несжимаемой жидкостью. .
. применяют формулу Кармана
применяют формулу Кармана ,
, можно пользоваться формулой Прандтля:
можно пользоваться формулой Прандтля: .
.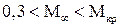 ). Расчет коэффициента сопротивления трения можно вести по приведенным выше зависимостям для несжимаемой жидкости, учитывая влияние сжимаемости по методу Прандтля–Глауэрта:
). Расчет коэффициента сопротивления трения можно вести по приведенным выше зависимостям для несжимаемой жидкости, учитывая влияние сжимаемости по методу Прандтля–Глауэрта: .
. ). При закритических скоростях появляется еще одна составляющая сопротивления – волновое сопротивление, т. е.
). При закритических скоростях появляется еще одна составляющая сопротивления – волновое сопротивление, т. е.  . Рассчитать коэффициент волнового сопротивления профиля можно по формуле
. Рассчитать коэффициент волнового сопротивления профиля можно по формуле .
. Наибольшим волновым сопротивлением при около- и сверхзвуковых скоростях обладают толстые дозвуковые профили. Основным принципом уменьшения волнового сопротивления является уменьшение возмущений, вносимых телом в поток за счет следующих факторов:
Наибольшим волновым сопротивлением при около- и сверхзвуковых скоростях обладают толстые дозвуковые профили. Основным принципом уменьшения волнового сопротивления является уменьшение возмущений, вносимых телом в поток за счет следующих факторов: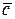 , что приводит к увеличению
, что приводит к увеличению  , где
, где  – составляющая, зависящая от угла атаки и не зависящая от формы профиля (
– составляющая, зависящая от угла атаки и не зависящая от формы профиля ( );
);  – оценивает вклад формы и толщины профиля (при
– оценивает вклад формы и толщины профиля (при  , (8.12)
, (8.12)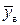 и нижнего
и нижнего  обводов профиля в зависимости от относительной продольной координаты
обводов профиля в зависимости от относительной продольной координаты  :
:  .
. в абсолютном или относительном виде.
в абсолютном или относительном виде. = 0,2…0,4.
= 0,2…0,4. (
( % в зависимости от назначения профиля).
% в зависимости от назначения профиля). (обычно
(обычно  ).
). – коэффициент подъемной силы;
– коэффициент подъемной силы; – коэффициент силы лобового сопротивления;
– коэффициент силы лобового сопротивления;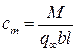 – коэффициент момента, где М – момент аэродинамической силы R относительно оси OZа;
– коэффициент момента, где М – момент аэродинамической силы R относительно оси OZа;  – скоростной напор невозмущенного набегающего потока; b – хорда профиля;
– скоростной напор невозмущенного набегающего потока; b – хорда профиля;  – плечо равнодействующей аэродинамической силы.
– плечо равнодействующей аэродинамической силы. , которое показывает соотношение между подъемной силой и силой лобового сопротивления профиля, крыла или летательного аппарата в целом. Величина К может изменяться от долей единицы (для бескрылых ЛА при больших углах атаки) до значений порядка 40...60 (для безмоторных ЛА – планеров или для ЛА с ограниченными запасами топлива, предназначенными для выполнения полетов большой протяженности).
, которое показывает соотношение между подъемной силой и силой лобового сопротивления профиля, крыла или летательного аппарата в целом. Величина К может изменяться от долей единицы (для бескрылых ЛА при больших углах атаки) до значений порядка 40...60 (для безмоторных ЛА – планеров или для ЛА с ограниченными запасами топлива, предназначенными для выполнения полетов большой протяженности).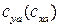 (рис. 8.2, б).
(рис. 8.2, б).
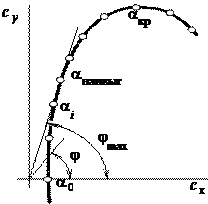
 и
и  профиль не создает подъемной силы. Увеличение угла атаки приводит к росту величины коэффициента подъемной силы. Зависимость
профиль не создает подъемной силы. Увеличение угла атаки приводит к росту величины коэффициента подъемной силы. Зависимость  имеет линейный характер, пока на поверхности профиля сохраняется безотрывный характер течения. В аналитическом виде линейную зависимость
имеет линейный характер, пока на поверхности профиля сохраняется безотрывный характер течения. В аналитическом виде линейную зависимость  , где
, где 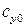 – коэффициент подъемной силы при нулевом угле атаки;
– коэффициент подъемной силы при нулевом угле атаки;  .
. величина
величина  . В этот момент отрыв потока охватывает всю верхнюю поверхность профиля.
. В этот момент отрыв потока охватывает всю верхнюю поверхность профиля. при разных углах атаки и оценить их соотношение через качество профиля. Угол
при разных углах атаки и оценить их соотношение через качество профиля. Угол  . Наибольшую величину угол
. Наибольшую величину угол  (а следовательно и качество профиля
(а следовательно и качество профиля  ) имеет для касательной, проведенной к поляре первого рода из начала координат. Угол атаки, обеспечивающий полет ЛА с качеством
) имеет для касательной, проведенной к поляре первого рода из начала координат. Угол атаки, обеспечивающий полет ЛА с качеством  полет ЛА происходит с наименьшими затратами мощности, т. е. с минимальным расходом топлива.
полет ЛА происходит с наименьшими затратами мощности, т. е. с минимальным расходом топлива.


