
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет пограничного слоя на плоской поверхности
В несжимаемой среде
Решение задачи об обтекании плоской пластинки в теории сопротивления играет большую роль. Найденная для пластинки зависимость
Для плоской пластинки (рис. 7.6) скорость потенциального течения
Для решения задачи о пограничном слое введем дополнительно еще два соотношения: 1) закон распределения скорости по толщине пограничного слоя 2) уравнение, связывающее касательное напряжение на стенке Вид этих соотношений зависит от состояния пограничного слоя.
Ламинарный пограничный слой
Рассмотрим закон распределения скорости в виде полинома третьей степени (метод Польгаузена)
Коэффициенты полинома Кинематические граничные условия: 1) при 2) при Динамические граничные условия: 1) при 2) при Подставляя указанные граничные условия в уравнения (7.11), получим следующую систему уравнений для определения коэффициентов
В результате ее решения определим значения коэффициентов:
Выражение для
Вычислим интегралы, входящие в интегральное соотношение:
и
Подставив эти интегралы в интегральное соотношение (7.10), получим обыкновенное дифференциальное уравнение:
Группируя подобные члены и разделяя переменные, получаем В итоге, после небольших преобразований получаем формулу для расчета толщины пограничного слоя:
Как следует из уравнения (7.13), толщина ламинарного пограничного слоя нарастает по параболическому закону. Тогда толщина вытеснения и толщина потери импульса для ламинарного пограничного слоя будут следующие: Введем в рассмотрение местный коэффициент трения
Подставив выражение (7.12) в выражение (7.14) с учетом уравнения (7.13), получаем следующее:
Формула (7.15) показывает, что местный коэффициент трения, имея максимум вблизи передней кромки, уменьшается при удалении от нее. Найдем силу трения, действующую на пластинку, учитывая тот факт, что пограничный слой есть на обеих сторонах пластинки (см. рис. 7.6). Запишем выражения для
и через касательные напряжения (или местный коэффициент трения):
Приравняв правые части этих выражений, получим зависимость для расчета коэффициента сопротивления трения плоской пластинки через местный коэффициент трения:
С учетом формулы (7.15) формула для коэффициента сопротивления трения плоской пластинки при ламинарном пограничном слое принимает вид
В уравнении (7.17) в качестве характерного линейного размера в числе Рейнольдса используется хорда пластинки
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.251.22 (0.008 с.) |
 и величина коэффициента сопротивления трения могут быть использованы при приближенных расчетах других удобообтекаемых тел.
и величина коэффициента сопротивления трения могут быть использованы при приближенных расчетах других удобообтекаемых тел. Задача расчета пограничного слоя в несжимаемой среде сводится к определению закона изменения толщины пограничного слоя, т. е.
Задача расчета пограничного слоя в несжимаемой среде сводится к определению закона изменения толщины пограничного слоя, т. е. 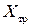 при условии, что известны скорость
при условии, что известны скорость  , величина коэффициента кинематической вязкости и хорда пластинки
, величина коэффициента кинематической вязкости и хорда пластинки  .
. , градиент давления вдоль пластинки
, градиент давления вдоль пластинки  (пластинка – тело с нулевым градиентом давления вдоль ее хорды). С учетом вышеизложенного интегральное соотношение (7.8) приобретает вид
(пластинка – тело с нулевым градиентом давления вдоль ее хорды). С учетом вышеизложенного интегральное соотношение (7.8) приобретает вид . (7.10)
. (7.10)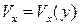 ;
; с толщиной пограничного слоя
с толщиной пограничного слоя  .
. . (7.11)
. (7.11) определим из граничных кинематических и динамических условий:
определим из граничных кинематических и динамических условий: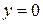 ,
,  ;
; ,
,  .
. и из первого уравнения системы (7.6) для пограничного слоя получаем
и из первого уравнения системы (7.6) для пограничного слоя получаем  , но
, но  и тогда
и тогда  ;
; обращаются в нуль, и отсюда
обращаются в нуль, и отсюда  .
. ,
, 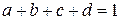 ,
, 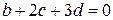 ,
, 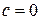 .
.

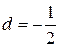 . Следовательно, закон распределения скорости по сечению ламинарного пограничного слоя принимает вид
. Следовательно, закон распределения скорости по сечению ламинарного пограничного слоя принимает вид . (7.11а)
. (7.11а) . Из уравнения (7.11а) производная
. Из уравнения (7.11а) производная  , отсюда:
, отсюда: . (7.12)
. (7.12)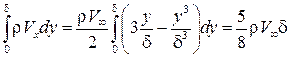

 .
.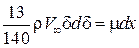 . После интегрирования имеем следующее:
. После интегрирования имеем следующее:  . Значение произвольной постоянной
. Значение произвольной постоянной  определим из условий на передней кромке пластинки: при
определим из условий на передней кромке пластинки: при  толщина пограничного слоя
толщина пограничного слоя  , следовательно
, следовательно  .
. , или
, или  . (7.13)
. (7.13) и
и  .
. , представляющий собой отношение касательных напряжений к скоростному напору:
, представляющий собой отношение касательных напряжений к скоростному напору: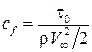 . (7.14)
. (7.14) или
или 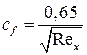 . (7.15)
. (7.15)
 .
. . (7.16)
. (7.16)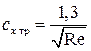 . (7.17)
. (7.17) .
.


