
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения напряженного состояния
Реальной жидкости
В уравнениях движения при учете внутреннего трения в жидкости фигурирует вектор
где Каждый из векторов
Для получения полной (разрешимой) системы дифференциальных уравнений движения реальной жидкости необходимо ввести уравнения, определяющие составляющие тензора напряжений и вектора теплового потока. Эти уравнения существенно зависят от характера движения жидкости (ламинарного или турбулентного). Ламинарное движение. При ламинарном движении трение и теплопередача определяются лишь движением молекул. При одномерном движении жидкости в направлении оси ОХ, сила трения, действующая на единицу площади, определяется по закону Ньютона (1.1):
Для пространственного движения, если считать, что составляющие тензора напряжений представляют собой линейные функции от составляющих тензора скоростей деформаций, получаем обобщенный закон Ньютона для касательных напряжений:
где Из тензора напряжений (3.10) с учетом уравнения (3.11) найдем сумму нормальных напряжений
Введем переменную
Количество тепла, переносимое в единицу времени через единицу площади в направлении оси У, определяется по закону Фурье:
В общем случае вектор теплового потока при ламинарном пространственном движении жидкости можно выразить через градиент температуры:
Турбулентное движение. При турбулентном движении жидкости трение и теплопроводность определяются как движением молекул, так и наличием перемешивания частиц жидкости (групп молекул). Для турбулентного движения характерно наличие пульсаций частиц и значений гидродинамических элементов в данной точке пространства. Точные уравнения связи тензора турбулентного трения и вектора Зафиксируем материальную точку пространства. Истинная скорость данной точки в данный момент времени равна
Разность между истинной и средней местной скоростью называется пульсационной составляющей скорости, или просто пульсацией
Турбулентные трение и теплопроводность обусловлены наличием пульсаций Возьмем два слоя жидкости на расстоянии l друг от друга (l – путь перемешивания частиц жидкости или среднее расстояние пульсаций). Истинные скорости в этом случае одномерного движения равны Изменение количества движения вследствие наличия пульсаций (обусловливающее появление турбулентного трения) равно
Перейдем к теплосодержанию. Теплосодержание единицы массы в слое 1 равно
Путь перемешивания l определяется таким образом, что
При решении конкретных задач относительно пути перемешивания l, делаются соответствующие предположения, проверяемые экспериментально по следствиям. Рассмотрим некоторые частные случаи. 1. Течение в пограничном слое. Для пограничного слоя считают, что путь перемешивания пропорционален нормальной к поверхности координате, т. е. 2. Истечение струи из отверстия. Это течение одномерное вдоль оси ОX. Вполне естественно предположить, что чем дальше течение от краев отверстия, тем больше пульсация. Поэтому можно предположить, что
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.105.194 (0.008 с.) |
 . Вектор касательных напряжений, действующих на площадку с нормалью
. Вектор касательных напряжений, действующих на площадку с нормалью  , обычно представляют как
, обычно представляют как , (3.9)
, (3.9) – векторы касательных напряжений, действующих на площадки, перпендикулярные соответствующим осям координат. Формулу (3.9) называют формулой Коши.
– векторы касательных напряжений, действующих на площадки, перпендикулярные соответствующим осям координат. Формулу (3.9) называют формулой Коши. (3.10)
(3.10) .
. (3.11)
(3.11) и
и  – координатные направления (в декартовой системе –
– координатные направления (в декартовой системе –  ,
,  , z);
, z);  – функция, которая может принимать лишь два значения: при
– функция, которая может принимать лишь два значения: при 
 , а при
, а при 
 ;
;  – проекции вектора скорости на соответствующие координатные направления.
– проекции вектора скорости на соответствующие координатные направления. :
: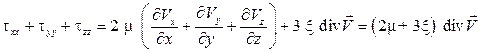 .
. , характеризующую напряжение, которое возникает в жидкости при объемном сжатии. Если в жидкости кроме давления нет других объемных напряжений, то
, характеризующую напряжение, которое возникает в жидкости при объемном сжатии. Если в жидкости кроме давления нет других объемных напряжений, то  и, следовательно,
и, следовательно, 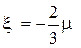 (гипотеза Стокса). В этом случае обобщенный закон Ньютона (3.11) можно переписать следующим образом:
(гипотеза Стокса). В этом случае обобщенный закон Ньютона (3.11) можно переписать следующим образом: . (3.12)
. (3.12) .
. .
. с соответствующими средними местными величинами до сих пор не установлены. Разобраны лишь простейшие случаи, основанные на полуэмпирической теории турбулентности.
с соответствующими средними местными величинами до сих пор не установлены. Разобраны лишь простейшие случаи, основанные на полуэмпирической теории турбулентности.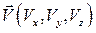 . Но приборами мы измеряем скорость не материальной точки, а некоторого объема жидкости, и не в данный момент времени, а в промежуток времени
. Но приборами мы измеряем скорость не материальной точки, а некоторого объема жидкости, и не в данный момент времени, а в промежуток времени  . Таким образом, мы определяем некоторую среднюю скорость в малом объеме
. Таким образом, мы определяем некоторую среднюю скорость в малом объеме  за время
за время  (промежуток осреднения), которая для одномерного течения жидкости равна
(промежуток осреднения), которая для одномерного течения жидкости равна .
. . Тогда истинная скорость будет равна сумме средней и пульсационной составляющей скорости, например,
. Тогда истинная скорость будет равна сумме средней и пульсационной составляющей скорости, например,  . В пространственном случае имеем следующее:
. В пространственном случае имеем следующее: .
.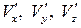 . Можно получить выражения для
. Можно получить выражения для  и
и  в случае турбулентного движения.
в случае турбулентного движения. . Из-за наличия пульсации
. Из-за наличия пульсации 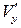 происходит перенос количества движения и теплосодержания из слоя в слой (турбулентное перемешивание). Через площадку, равную единице площади, в единицу времени переносится масса жидкости, равная
происходит перенос количества движения и теплосодержания из слоя в слой (турбулентное перемешивание). Через площадку, равную единице площади, в единицу времени переносится масса жидкости, равная 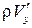 . Количество движения этой массы в слое 1 равно
. Количество движения этой массы в слое 1 равно  , а в слое 2 –
, а в слое 2 –  .
. .
. , а в слое 2 –
, а в слое 2 –  . Для переносимой из слоя в слой массы
. Для переносимой из слоя в слой массы  и
и  . Изменение теплосодержания (перенос тепла) определим как:
. Изменение теплосодержания (перенос тепла) определим как: .
. . Затем предполагаем одинаковость порядка
. Затем предполагаем одинаковость порядка  и
и 
 . В результате получаем основные соотношения полуэмпирической теории турбулентности:
. В результате получаем основные соотношения полуэмпирической теории турбулентности: .
.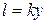
 0,39 y, где k – коэффициент пропорциональности, не зависящий от числа Рейнольдса. Явно, что пульсации больше там, где больше скорость. Следовательно, на нижней границе пограничного слоя (у стенки) пульсация равна нулю.
0,39 y, где k – коэффициент пропорциональности, не зависящий от числа Рейнольдса. Явно, что пульсации больше там, где больше скорость. Следовательно, на нижней границе пограничного слоя (у стенки) пульсация равна нулю. , где с есть некоторая постоянная, c = const.
, где с есть некоторая постоянная, c = const.


