
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение, выражающее закон измененияСтр 1 из 6Следующая ⇒ Глава 3 УРАВНЕНИЯ ДВИЖЕНИЯ ГАЗА КАК СПЛОШНОЙ СРЕДЫ
Уравнения движения выводятся исходя из закона сохранения массы, закона изменения количества движения, закона сохранения энергии, уравнения термодинамического состояния и уравнения напряженного состояния. Применим эти законы к массе жидкости m, находящейся в момент времени t в некотором произвольно выделенном объеме V. Будем считать, что внутри объема нет ни источников, ни стоков.
Уравнение неразрывности
Согласно закону сохранения массы для изолированной системы, масса жидкости m, которая находилась в момент времени t в рассматриваемом объеме, будет оставаться неизменной при ее движении. То есть
Найдем изменение массы за счет изменения объема. Элемент поверхности dS рассматриваемого объема переместится за время Преобразуем интеграл по площади в интеграл по объему с помощью формулы Остроградского–Гаусса:
Объединяя интегралы, получим
Выражение (3.1) представляет собой закон сохранения массы в дифференциальной форме, или иначе – уравнение неразрывности для неустановившегося движения сжимаемой жидкости. Для установившегося движения сжимаемой жидкости уравнение неразрывности имеет вид
Приведем уравнение (3.1) к другой форме, произведя следующие преобразования:
Так как
В случае движения несжимаемой жидкости (
Если движение несжимаемой жидкости потенциальное, то проекции вектора скорости на координатные направления можно записать через потенциал вектора скорости
Тогда
В случае установившегося движения газа при решении практических задач часто используется уравнение неразрывности в форме уравнения массового расхода:
где F – площадь поперечного сечения трубки тока, или (при движении несжимаемой среды) в форме объемного расхода:
Формулы (3.2) и (3.2а) получаются элементарным образом при рассмотрении расхода сжимаемой и несжимаемой жидкости через поперечные сечения трубки тока.
Количества движения
Согласно закону изменения количества движения изменение вектора количества движения
Внешние силы, способные изменить количество движения данной массы жидкости, разделяют на объемные и поверхностные силы. Объемные силы – силы, величина которых пропорциональна массе жидкости в выделенном объеме. В данном случае имеет место сила тяжести, равная Поверхностные силы – силы, величина которых пропорциональна площади поверхности, охватывающей выделенный объем. К ним относятся силы от нормальных и касательных напряжений, действующих на поверхность частицы. Считая жидкость идеальной, ограничимся рассмотрением только силы от аэродинамического давления, которая направлена по внутренней нормали. Тогда для внешней нормали Если
Подставляя все в уравнение (3.3), получаем уравнение движения идеальной жидкости в интегральной форме:
Применив формулу Остроградского–Гаусса
В силу произвольности выделенного объема получаем, чтоподынтегральное выражение равно нулю в каждой точке газового потока в любой момент времени. Таким образом, можно прийти к уравнению движения идеального газа в векторной форме – уравнению движения Эйлера:
Запишем уравнение (3.5) в проекциях на оси декартовой системы координат. Так как
Уравнения (3.6) применимы для исследования движения сжимаемой и несжимаемой жидкости. Каждый член этой системы уравнений представляет собой ускорение. Можно сказать, что при движении идеальной жидкости суммарное ускорение складывается из ускорения от массовых сил и ускорения от сил давления. Преобразуем левые части уравнений (3.6) с учетом формулы (2.3). При этом вспомним, что для проекции ускорения на ось ОХ
Применив аналогичную запись для других проекций, получим дифференциальные уравнения Эйлера в развернутом виде:
При интегрировании дифференциальных уравнений движения газа получим решения, содержащие произвольные функции и произвольные постоянные. Для их определения необходимы дополнительные условия: начальные и граничные. При начальных условиях задается поле скоростей в начальный для данной задачи момент времени, т. е. при t = 0:
Очевидно, что начальные условия необходимы при решении задач неустановившегося движения газа. Граничные условия – это условия на некоторых границах течения, в качестве которых может выступать поверхность обтекаемого тела, невозмущенный набегающий поток, поверхности раздела потоков и др. Граничные условия подразделяют на динамические и кинематические. Динамические условия относятся к силам. Например, на свободной поверхности имеет место равенство давления внешней среды и давления на обтекаемой поверхности. Кинематические условия относятся к скоростям. Например, на поверхности обтекаемого тела должно выполняться условие безотрывности обтекания или условие непротекания Если рассматривается движение вязкой жидкости, то в уравнениях движения необходимо учесть внутреннее трение в жидкости через силу трения:
где
Тогда уравнение (3.4) примет вид
После интегрирования и преобразований уравнение движения реальной жидкости в векторной форме запишется следующим образом:
Реальной жидкости
В уравнениях движения при учете внутреннего трения в жидкости фигурирует вектор
где Каждый из векторов
Для получения полной (разрешимой) системы дифференциальных уравнений движения реальной жидкости необходимо ввести уравнения, определяющие составляющие тензора напряжений и вектора теплового потока. Эти уравнения существенно зависят от характера движения жидкости (ламинарного или турбулентного). Ламинарное движение. При ламинарном движении трение и теплопередача определяются лишь движением молекул. При одномерном движении жидкости в направлении оси ОХ, сила трения, действующая на единицу площади, определяется по закону Ньютона (1.1):
Для пространственного движения, если считать, что составляющие тензора напряжений представляют собой линейные функции от составляющих тензора скоростей деформаций, получаем обобщенный закон Ньютона для касательных напряжений:
где Из тензора напряжений (3.10) с учетом уравнения (3.11) найдем сумму нормальных напряжений
Введем переменную
Количество тепла, переносимое в единицу времени через единицу площади в направлении оси У, определяется по закону Фурье:
В общем случае вектор теплового потока при ламинарном пространственном движении жидкости можно выразить через градиент температуры:
Турбулентное движение. При турбулентном движении жидкости трение и теплопроводность определяются как движением молекул, так и наличием перемешивания частиц жидкости (групп молекул). Для турбулентного движения характерно наличие пульсаций частиц и значений гидродинамических элементов в данной точке пространства. Точные уравнения связи тензора турбулентного трения и вектора Зафиксируем материальную точку пространства. Истинная скорость данной точки в данный момент времени равна
Разность между истинной и средней местной скоростью называется пульсационной составляющей скорости, или просто пульсацией
Турбулентные трение и теплопроводность обусловлены наличием пульсаций Возьмем два слоя жидкости на расстоянии l друг от друга (l – путь перемешивания частиц жидкости или среднее расстояние пульсаций). Истинные скорости в этом случае одномерного движения равны Изменение количества движения вследствие наличия пульсаций (обусловливающее появление турбулентного трения) равно
Перейдем к теплосодержанию. Теплосодержание единицы массы в слое 1 равно
Путь перемешивания l определяется таким образом, что
При решении конкретных задач относительно пути перемешивания l, делаются соответствующие предположения, проверяемые экспериментально по следствиям. Рассмотрим некоторые частные случаи. 1. Течение в пограничном слое. Для пограничного слоя считают, что путь перемешивания пропорционален нормальной к поверхности координате, т. е. 2. Истечение струи из отверстия. Это течение одномерное вдоль оси ОX. Вполне естественно предположить, что чем дальше течение от краев отверстия, тем больше пульсация. Поэтому можно предположить, что
Интеграл Лагранжа
Так как при потенциальном движении угловая скорость вращательного движения равна нулю, то
Считая жидкость идеальной, обратимся к системе уравнений Эйлера в развернутом виде (3.7). Рассмотрим уравнение в проекции на ось ОХ:
Принимая во внимание условия (3.23), конвективную производную в уравнении (3.24) приведем к виду
Аналогичные преобразования проведем для конвективных производных уравнений в проекциях на оси ОУ и ОZ. Подставим полученные выражения в уравнения Эйлера:
Преобразуем локальные производные в уравнениях (3.25), учитывая, что при потенциальном движении проекции скорости можно представить через потенциал скорости
и свойство независимости смешанной производной от порядка дифференцирования:
Введем в рассмотрение такое понятие, как баротропность. Баротропным называется движение, при котором плотность В системе уравнений (3.25) произведем замены с помощью функции давления. Умножив каждое из уравнений на соответствующее приращение (dx, dy, dz)
после их сложения получим следующее:
Выражение в скобках
Таким образом, уравнение (3.26) запишется в следующем виде:
После интегрирования получим
т. е. интеграл Лагранжа для потенциального неустановившегося движения сжимаемой среды. Для несжимаемой среды
При установившемся движении сжимаемой жидкости вместо произвольной функции имеем постоянную интегрирования, и интеграл Лагранжа примет вид интеграла Эйлера–Бернулли:
где Через малое отверстие
Рассмотрим истечение газа из сосуда неограниченных размеров через малое отверстие с площадью поперечного сечения – условие изоэнтропичности – интеграл Бернулли в виде Тогда скорость истечения газа из сосуда через отверстие равна
а массовый расход газа
Определим, при каком отношении давлений
Очевидно, что максимальное значение расход газа имеет тогда, когда полученная производная обращается в нуль, т. е. когда сомножитель в квадратной скобке последнего выражения равен нулю. Отсюда получаем, что
Элементарное объяснение возникновения подъемной силы
Воспользуемся уравнением Бернулли для несжимаемой жидкости Так как Оценка влияния сжимаемости
Выясним, примерно до каких скоростей можно рассматривать газ как несжимаемую жидкость. Из уравнения Бернулли для несжимаемой жидкости
Определим теперь давление торможения
Так как влиянием сжимаемости можно пренебречь только при достаточно малых числах Маха, примем, что М << 1 и разложим выражение для
+
Отсюда
где
Таблица 3.1 Погрешности определения давления без учета сжимаемости газа
Допуская ошибку при определении Таким образом, мы познакомились со всеми уравнениями, описывающими движение газа как сплошной среды. В следующей главе будет рассмотрен случай одномерного движения газа.
Контрольные вопросы и задания
1. Какие силы, действующие на рассматриваемый объем газа, относятся к поверхностным силам, а какие – к объемным (массовым)? 2. Дайте определение и запишите первый закон термодинамики. 3. Назовите закон сохранения, который был использован при выводе уравнения неразрывности. В чем его суть? 4. При выводе уравнения, выражающего закон сохранения энергии, были введены следующие понятия: 5. Для того, чтобы некоторый процесс был адиабатическим, необходимо соблюдение следующих условий: 6. Какую физическую величину называют удельной теплоемкостью? Что больше: удельная теплоемкость при постоянном давлении 7. При интегрировании дифференциальных уравнений Эйлера для частных случаев движения жидкости были получены интеграл Эйлера–Бернулли и интеграл Бернулли, имеющие одинаковую запись: 8. Какое движение жидкости называется баротропным? Для каких термодинамических процессов можно ввести это понятие? 9. До каких чисел Маха можно рассматривать воздух как несжимаемую жидкость, т. е. проводить определение давления без учета сжимаемости среды? Какова в этом случае предельная скорость движения воздуха (м/с) при нормальных условиях? 10. Глава 3 УРАВНЕНИЯ ДВИЖЕНИЯ ГАЗА КАК СПЛОШНОЙ СРЕДЫ
Уравнения движения выводятся исходя из закона сохранения массы, закона изменения количества движения, закона сохранения энергии, уравнения термодинамического состояния и уравнения напряженного состояния. Применим эти законы к массе жидкости m, находящейся в момент времени t в некотором произвольно выделенном объеме V. Будем считать, что внутри объема нет ни источников, ни стоков.
Уравнение неразрывности
Согласно закону сохранения массы для изолированной системы, масса жидкости m, которая находилась в момент времени t в рассматриваемом объеме, будет оставаться неизменной при ее движении. То есть
Найдем изменение массы за счет изменения объема. Элемент поверхности dS рассматриваемого объема переместится за время Преобразуем интеграл по площади в интеграл по объему с помощью формулы Остроградского–Гаусса:
Объединяя интегралы, получим
Выражение (3.1) представляет собой закон сохранения массы в дифференциальной форме, или иначе – уравнение неразрывности для неустановившегося движения сжимаемой жидкости. Для установившегося движения сжимаемой жидкости уравнение неразрывности имеет вид
Приведем уравнение (3.1) к другой форме, произведя следующие преобразования:
| Поделиться:
| |
 и
и  .
. Изменение массы при движении может происходить как за счет изменения плотности
Изменение массы при движении может происходить как за счет изменения плотности  с течением времени, так и за счет изменения объема V, который может занимать рассматриваемая масса жидкости в следующий момент времени. Изменение массы за счет изменения плотности запишется как
с течением времени, так и за счет изменения объема V, который может занимать рассматриваемая масса жидкости в следующий момент времени. Изменение массы за счет изменения плотности запишется как  .
. на расстояние
на расстояние  (рис. 3.1); за счет перемещения элемента поверхности объем изменится в единицу времени на
(рис. 3.1); за счет перемещения элемента поверхности объем изменится в единицу времени на  . Тогда изменение массы равно
. Тогда изменение массы равно  . Поскольку суммарное изменение массы равно нулю, то получаем
. Поскольку суммарное изменение массы равно нулю, то получаем  – закон сохранения массы в интегральной форме.
– закон сохранения массы в интегральной форме. .
.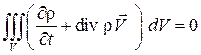 . В силу произвольности элементарного объема
. В силу произвольности элементарного объема  это равенство возможно, если подынтегральное выражение равно нулю, т. е. если
это равенство возможно, если подынтегральное выражение равно нулю, т. е. если . (3.1)
. (3.1) . (3.1а)
. (3.1а)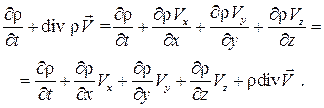
 , то уравнение неразрывности примет вид
, то уравнение неразрывности примет вид . (3.1б)
. (3.1б) ) запись уравнения неразрывности еще более упростится:
) запись уравнения неразрывности еще более упростится: . (3.1в)
. (3.1в) как
как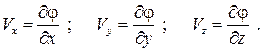
 . Так как
. Так как  – это оператор Лапласа, то уравнение неразрывности для случая потенциального движения несжимаемой жидкости преобразуется в уравнение Лапласа:
– это оператор Лапласа, то уравнение неразрывности для случая потенциального движения несжимаемой жидкости преобразуется в уравнение Лапласа: . (3.1г)
. (3.1г) , (3.2)
, (3.2) . (3.2а)
. (3.2а) постоянной массы m (находящейся в объеме V в момент времени t) равно сумме внешних сил, действующих на рассматриваемую массу:
постоянной массы m (находящейся в объеме V в момент времени t) равно сумме внешних сил, действующих на рассматриваемую массу: . (3.3)
. (3.3) , где
, где  – главный вектор массовых сил, отнесенных к единице массы, т. е. ускорение от массовых сил (наиболее простое представление – ускорение силы тяжести).
– главный вектор массовых сил, отнесенных к единице массы, т. е. ускорение от массовых сил (наиболее простое представление – ускорение силы тяжести). коэффициент давления
коэффициент давления  , и сила, действующая на всю поверхность, равна
, и сила, действующая на всю поверхность, равна  .
.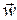 есть ускорение элемента dV, то сила инерции (вектор изменения количества движения) равна
есть ускорение элемента dV, то сила инерции (вектор изменения количества движения) равна .
. .
. , можем объединить все три интеграла:
, можем объединить все три интеграла: . (3.4)
. (3.4)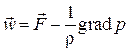 . (3.5)
. (3.5) ,
,  ,
,  , то в проекциях на оси координат уравнения Эйлера запишутся в виде
, то в проекциях на оси координат уравнения Эйлера запишутся в виде . (3.6)
. (3.6)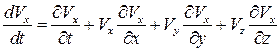 .
. (3.7)
(3.7)
 , в силу которых вектор скорости направлен по касательной к поверхности.
, в силу которых вектор скорости направлен по касательной к поверхности.
 – вектор силы трения, действующей на единичную площадку,положение которой определяется в пространстве нормалью
– вектор силы трения, действующей на единичную площадку,положение которой определяется в пространстве нормалью  .
. .
. . (3.8)
. (3.8) , (3.9)
, (3.9) – векторы касательных напряжений, действующих на площадки, перпендикулярные соответствующим осям координат. Формулу (3.9) называют формулой Коши.
– векторы касательных напряжений, действующих на площадки, перпендикулярные соответствующим осям координат. Формулу (3.9) называют формулой Коши. (3.10)
(3.10) .
. (3.11)
(3.11) и
и  – координатные направления (в декартовой системе –
– координатные направления (в декартовой системе –  ,
,  , z);
, z);  – функция, которая может принимать лишь два значения: при
– функция, которая может принимать лишь два значения: при 
 , а при
, а при 
 ;
;  – проекции вектора скорости на соответствующие координатные направления.
– проекции вектора скорости на соответствующие координатные направления. :
: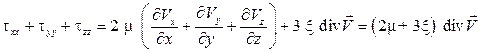 .
. , характеризующую напряжение, которое возникает в жидкости при объемном сжатии. Если в жидкости кроме давления нет других объемных напряжений, то
, характеризующую напряжение, которое возникает в жидкости при объемном сжатии. Если в жидкости кроме давления нет других объемных напряжений, то  и, следовательно,
и, следовательно, 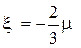 (гипотеза Стокса). В этом случае обобщенный закон Ньютона (3.11) можно переписать следующим образом:
(гипотеза Стокса). В этом случае обобщенный закон Ньютона (3.11) можно переписать следующим образом: . (3.12)
. (3.12) .
. .
. с соответствующими средними местными величинами до сих пор не установлены. Разобраны лишь простейшие случаи, основанные на полуэмпирической теории турбулентности.
с соответствующими средними местными величинами до сих пор не установлены. Разобраны лишь простейшие случаи, основанные на полуэмпирической теории турбулентности.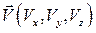 . Но приборами мы измеряем скорость не материальной точки, а некоторого объема жидкости, и не в данный момент времени, а в промежуток времени
. Но приборами мы измеряем скорость не материальной точки, а некоторого объема жидкости, и не в данный момент времени, а в промежуток времени  . Таким образом, мы определяем некоторую среднюю скорость в малом объеме
. Таким образом, мы определяем некоторую среднюю скорость в малом объеме  за время
за время  (промежуток осреднения), которая для одномерного течения жидкости равна
(промежуток осреднения), которая для одномерного течения жидкости равна .
. . Тогда истинная скорость будет равна сумме средней и пульсационной составляющей скорости, например,
. Тогда истинная скорость будет равна сумме средней и пульсационной составляющей скорости, например,  . В пространственном случае имеем следующее:
. В пространственном случае имеем следующее: .
.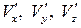 . Можно получить выражения для
. Можно получить выражения для  и
и  в случае турбулентного движения.
в случае турбулентного движения. . Из-за наличия пульсации
. Из-за наличия пульсации 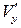 происходит перенос количества движения и теплосодержания из слоя в слой (турбулентное перемешивание). Через площадку, равную единице площади, в единицу времени переносится масса жидкости, равная
происходит перенос количества движения и теплосодержания из слоя в слой (турбулентное перемешивание). Через площадку, равную единице площади, в единицу времени переносится масса жидкости, равная 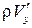 . Количество движения этой массы в слое 1 равно
. Количество движения этой массы в слое 1 равно  , а в слое 2 –
, а в слое 2 –  .
. .
. , а в слое 2 –
, а в слое 2 –  . Для переносимой из слоя в слой массы
. Для переносимой из слоя в слой массы  и
и  . Изменение теплосодержания (перенос тепла) определим как:
. Изменение теплосодержания (перенос тепла) определим как: .
. . Затем предполагаем одинаковость порядка
. Затем предполагаем одинаковость порядка  и
и 
 . В результате получаем основные соотношения полуэмпирической теории турбулентности:
. В результате получаем основные соотношения полуэмпирической теории турбулентности: .
.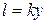
 0,39 y, где k – коэффициент пропорциональности, не зависящий от числа Рейнольдса. Явно, что пульсации больше там, где больше скорость. Следовательно, на нижней границе пограничного слоя (у стенки) пульсация равна нулю.
0,39 y, где k – коэффициент пропорциональности, не зависящий от числа Рейнольдса. Явно, что пульсации больше там, где больше скорость. Следовательно, на нижней границе пограничного слоя (у стенки) пульсация равна нулю. , где с есть некоторая постоянная, c = const.
, где с есть некоторая постоянная, c = const. , и из выражений (2.9) для составляющих угловой скорости имеем следующее:
, и из выражений (2.9) для составляющих угловой скорости имеем следующее: ,
,  ,
,  . (3.23)
. (3.23) . (3.24)
. (3.24) .
. ,
,  ,
, . (3.25)
. (3.25)
 ,
,  ,
, .
. . Следовательно,
. Следовательно,  и отсюда
и отсюда  .
.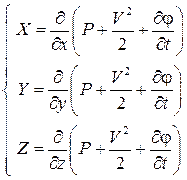

 (3.26)
(3.26) в правой части уравнения является функцией
в правой части уравнения является функцией  и t, но, считая, что параметры течения на данномэтапе не зависят от t, правую часть уравнения (3.26) можно считать полным дифференциалом некоторой функции
и t, но, считая, что параметры течения на данномэтапе не зависят от t, правую часть уравнения (3.26) можно считать полным дифференциалом некоторой функции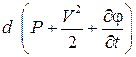 .
. . Так как правая часть этого уравнения есть полный дифференциал, то и левая часть также является полным дифференциалом некоторой функции Ф:
. Так как правая часть этого уравнения есть полный дифференциал, то и левая часть также является полным дифференциалом некоторой функции Ф: .
. , где C (t) – произвольная функция интегрирования, зависящая от t. Таким образом, мы восстанавливаем зависимость параметров течения от времени.С учетом выражения для функции давления получаем
, где C (t) – произвольная функция интегрирования, зависящая от t. Таким образом, мы восстанавливаем зависимость параметров течения от времени.С учетом выражения для функции давления получаем
 и интеграл Лагранжа для несжимаемой жидкости запишется следующим образом:
и интеграл Лагранжа для несжимаемой жидкости запишется следующим образом: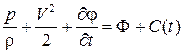 .
. ,
, для всей массы движущегося газа.
для всей массы движущегося газа. . Параметры состояния внутри сосуда –
. Параметры состояния внутри сосуда –  . Определим расход
. Определим расход  газа при установившемся характере истечения. Обозначим через
газа при установившемся характере истечения. Обозначим через  давление, плотность и скорость газа на выходе из отверстия. В качестве исходных уравнений запишем следующее:
давление, плотность и скорость газа на выходе из отверстия. В качестве исходных уравнений запишем следующее: , откуда
, откуда  ;
; .
.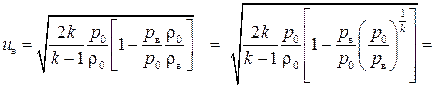
 ,
,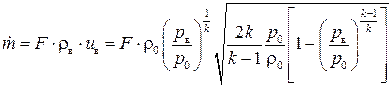 . (3.32)
. (3.32) массовый расход имеет максимальное значение
массовый расход имеет максимальное значение  . Возьмем производную от выражения (3.32) и приравняем ее к нулю:
. Возьмем производную от выражения (3.32) и приравняем ее к нулю:

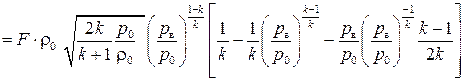 .
. , или
, или  , т. е. максимум расхода достигается при значении отношения давлений
, т. е. максимум расхода достигается при значении отношения давлений .
. Если
Если  мало отличается от давления окружающей среды
мало отличается от давления окружающей среды  , то давление в струе газа на выходе из отверстия устанавливается равным
, то давление в струе газа на выходе из отверстия устанавливается равным  и расход определяется по формуле (3.32). Если далее уменьшать
и расход определяется по формуле (3.32). Если далее уменьшать  ), то расход будет возрастать (рис. 3.2), достигнув максимума при давлении
), то расход будет возрастать (рис. 3.2), достигнув максимума при давлении  . Дальнейшее понижение
. Дальнейшее понижение  давление на выходе из отверстия всегда равно
давление на выходе из отверстия всегда равно  .
. Рассмотрим обтекание профиля несжимаемой жидкостью
Рассмотрим обтекание профиля несжимаемой жидкостью  . В передней критической точке О (рис. 3.3) центральная струйка разветвляется на две: ОАВ и ОDВ. Путь ОАВ > ОDВ, а частицы жидкости, разделившись в точке О, должны одновременно встретиться в точке В (в силу уравнения неразрывности). Тогда средняя скорость движения частиц вдоль верней части профиля должна быть больше, чем вдоль нижней (
. В передней критической точке О (рис. 3.3) центральная струйка разветвляется на две: ОАВ и ОDВ. Путь ОАВ > ОDВ, а частицы жидкости, разделившись в точке О, должны одновременно встретиться в точке В (в силу уравнения неразрывности). Тогда средняя скорость движения частиц вдоль верней части профиля должна быть больше, чем вдоль нижней ( ).
). . Записав его для верхней и нижней частей профиля
. Записав его для верхней и нижней частей профиля 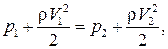 получим, что
получим, что  , т. е. давление на нижней стороне профиля больше, чем на верхней. Этот перепад давления и приводит к появлению равнодействующей, направленной вверх, – подъемной силы.
, т. е. давление на нижней стороне профиля больше, чем на верхней. Этот перепад давления и приводит к появлению равнодействующей, направленной вверх, – подъемной силы. , т. е. еще раз подтверждается вывод, что для создания подъемной силы необходимо, чтобы Г
, т. е. еще раз подтверждается вывод, что для создания подъемной силы необходимо, чтобы Г  .
. расчетная формула для давления торможения получается автоматически:
расчетная формула для давления торможения получается автоматически: . (3.33)
. (3.33) После преобразований формула для расчета полного давления в сжимаемом газе выглядит следующим образом:
После преобразований формула для расчета полного давления в сжимаемом газе выглядит следующим образом: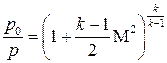 .
. по формуле бинома Ньютона:
по формуле бинома Ньютона:

 и при
и при  получаем выражение
получаем выражение  , которое представим в виде
, которое представим в виде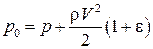 , (3.34)
, (3.34)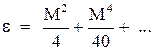 Сравнивая формулы (3.33) и (3.34), можно заметить, что
Сравнивая формулы (3.33) и (3.34), можно заметить, что  представляет собой погрешность, отнесенную к скоростному напору, при определении давления торможения без учета сжимаемости. Темпы роста величины погрешности с увеличением числа Маха можно проследить по приведенным данным (табл. 3.1).
представляет собой погрешность, отнесенную к скоростному напору, при определении давления торможения без учета сжимаемости. Темпы роста величины погрешности с увеличением числа Маха можно проследить по приведенным данным (табл. 3.1). – теплосодержание единицы массы движущейся жидкости;
– теплосодержание единицы массы движущейся жидкости;  – теплосодержание единицы массы покоящейся жидкости. Как эти понятия стыкуются с такими энергетическими характеристиками, как энтальпия
– теплосодержание единицы массы покоящейся жидкости. Как эти понятия стыкуются с такими энергетическими характеристиками, как энтальпия  (энтальпия торможения)?
(энтальпия торможения)? и
и  , где
, где  или удельная теплоемкость при постоянном объеме
или удельная теплоемкость при постоянном объеме  ? Каким образом связаны удельные теплоемкости
? Каким образом связаны удельные теплоемкости 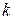 и
и  ?
? Что можно сказать о величине расхода воздуха, вытекающего из сосуда через малое отверстие, если давление в окружающей среде на выходе из отверстия
Что можно сказать о величине расхода воздуха, вытекающего из сосуда через малое отверстие, если давление в окружающей среде на выходе из отверстия  ? Чему при этом равно давление
? Чему при этом равно давление  в струе на выходе из отверстия?
в струе на выходе из отверстия?


