
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение уравнений.
Для численного решения уравнений, в тех случаях, когда трансцендентные уравнения не имеют аналитических решений, используется специальная команда fsolve(eq,x), параметры которой такие же, как и команды solve. Например: > x:=fsolve(cos(x)=x,x); x: =. 7390851332
Решение рекуррентных и функциональных уравнений. Команда rsolve(eq,f) позволяет решить рекуррентное уравнение eq для целой функции f. Можно задать некоторое начальное условие для функции f(n), тогда получиться частное решение данного рекуррентного уравнения. Например: > eq:=2*f(n)=3*f(n-1)-f(n-2);
> rsolve({eq,f(1)=0,f(2)=1},f);
Универсальная команда solve позволяет решать функциональные уравнения, например: > F:=solve(f(x)^2-3*f(x)+2*x,f); F:= proc (x) RootOf(_ Z ^2 - 3*_ Z + 2* x) end В результате получается решение в неявном виде. Однако Maple может работать с такими решениями. Неявное решение функционального уравнения можно попытаться преобразовать в какую-либо элементарную функцию с помощью команды convert. Продолжая приведенный выше пример, можно получить решение в явном виде: > f:=convert(F(x),radical);
Решение тригонометрических уравнений. Команда solve, примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале [0,2p]. Для того, чтобы получить все решения, следует предварительно ввести дополнительную команду _EnvAllSolutions:=true. Например: > _EnvAllSolutions:=true: > solve(sin(x)=cos(x),x);
В Maple символ _ Z ~ обозначает константу целого типа, поэтому решение данного уравнения в привычной форме имеет вид
Решение трансцендентных уравнений. При решении трансцендентных уравнений для получения решения в явном виде перед командой solve следует ввести дополнительную команду _EnvExplicit:=true. Пример решения сложной системы трансцендентных уравнений и упрощения вида решений: > eq:={ 7*3^x-3*2^(z+y-x+2)=15, 2*3^(x+1)+ 3*2^(z+y-x)=66, ln(x+y+z)-3*ln(x)-ln(y*z)=-ln(4) }: > _EnvExplicit:=true: > s:=solve(eq,{x,y,z}): > simplify(s[1]);simplify(s[2]); { x =2, y =3, z =1}, { x =2, y =1, z =3}
Задание 3. 1. Найти все решения системы уравнений Наберите: > eq:={x^2-y^2=1,x^2+x*y=2}; > _EnvExplicit:=true: > s:=solve(eq,{x,y});
Теперь найдите сумму двух наборов решений. Наберите: > x1:=subs(s[1],x): y1:=subs(s[1],y): x2:=subs(s[2],x): y2:=subs(s[2],y): > x1+x2; y1+y2; Чему равны эти суммы решений? 2. Численно решите уравнение
> x=fsolve(x^2=cos(x),x); x =.8241323123 3. Найдите функцию f (x), удовлетворяющую уравнению > F:=solve(f(x)^2-2*f(x)=x,f); F:= proc (x) RootOf(_ Z ^2-2*_ Z - x) end > f:=convert(F(x), radical);
4. Найдите все решения уравнения > _EnvAllSolutions:=true: > solve(5*sin(x)+12*cos(x)=13,x);
§4. Решение неравенств
Решение простых неравенств. Команда solve применяется также для решения неравенств. Решение неравенства выдается в виде интервала изменения искомой переменной. В том случае, если решение неравенства полуось, то в поле вывода появляется конструкция вида RealRange(–¥, Open(a)), которая означает, что x Î(–¥, a), а – некоторое число. Слово Open означает, что интервал с открытой границей. Если этого слова нет, то соответствующая граница интервала включена во множество решений. Например: > s:=solve(sqrt(x+3)<sqrt(x-1)+sqrt(x-2),x): > convert(s,radical); RealRange Если вы хотите получить решение неравенства не в виде интервального множества типа x Î(a, b), а в виде ограничений для искомой переменной типа a < x, x < b, то переменную, относительно которой следует разрешить неравенство, следует указывать в фигурных скобках. Например: > solve(1-1/2*ln(x)>2,{x});
Решение систем неравенств. С помощью команды solve можно также решить систему неравенств. Например: > solve({x+y>=2,x-2*y<=1,x-y>=0,x-2*y>=1},{x,y});
Задание 4. 1. Решите неравенство > solve(13*x^3-25*x^2-x^4-129*x+270>0,x); RealRange(Open(-3), Open(2)), RealRange(Open(5), Open(9)) Запишите этот результат в аналитическом виде. Получите решение этого неравенства в виде ограничений для искомой переменной. Проделайте это самостоятельно. 2. Решите неравенство > solve(exp(2*x+3)<1,x); RealRange Теперь получите самостоятельно решение этого неравенства в виде ограничений для искомой переменной. 3. Выполните все контрольные задания. Перед их выполнением наберите в текстовом режиме «Контрольные задания». Результаты выполнения заданий покажите преподавателю. Сохраните файл со всеми выполненными заданиями на диск. Ответьте на все контрольные вопросы.
Контрольные задания. 1. Дано комплексное число 2. Записать функцию
3. Записать функцию 4. Найти все точные решения системы 5. Найти все решения тригонометрического уравнения 6. Найти численное решение уравнения 7. Решить неравенство
Контрольные вопросы. 1. Опишите способы задания функций в Maple. 2. Какие операции оценивания производятся в Maple с действительными выражениями? 3. Для чего предназначена команда evalf? 4. С помощью каких команд можно найти вещественную и мнимую части комплексного выражения, а также его модуль и аргумент, и комплексно сопряженное ему число? Какую роль выполняет команда evalc? 5. Для чего предназначена команда solve? 6. Какие команды используются для численного решения уравнений и для решения рекуррентных уравнений? 7. Какие дополнительные команды следует ввести для того, чтобы получить точное решение уравнения, все решения уравнения? 8. В каком виде выдается решение неравенства? Как отличить в строке вывода закрытый интервал от открытого?
III. Построение графиков
1. Двумерные графики. 2. Трехмерные графики. Анимация.
§1. Двумерные графики
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 295; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.82.23 (0.018 с.) |



 ~
~ , где n – целые числа.
, где n – целые числа.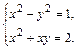
 ,
, 
 . Наберите:
. Наберите: . Наберите:
. Наберите:
 . Наберите:
. Наберите: ~
~


 . Наберите:
. Наберите: . Наберите:
. Наберите:
 . Найти его вещественную и мнимые части, алгебраическую форму, модуль и аргумент.
. Найти его вещественную и мнимые части, алгебраическую форму, модуль и аргумент. в виде функционального оператора и вычислите ее значения при x =1, y =0 и при
в виде функционального оператора и вычислите ее значения при x =1, y =0 и при  ,
,  .
. с помощью оператора присваивания и вычислите ее значение при x = a, y =1/ a, используя команду подстановки subs.
с помощью оператора присваивания и вычислите ее значение при x = a, y =1/ a, используя команду подстановки subs. в аналитическом виде.
в аналитическом виде. .
. .
. .
.


