
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели систем массового обслуживания. Определение оптимального числа причалов.
Многие экономические задачи связаны с системами массового обслуживания, в которых происходит удовлетворение требований на выполнение каких-либо услуг. Исследованием систем массового обслуживания (СМО) занимается теория очередей, на начальное развитие которой оказали особое влияние труды датского ученого А.К. Эрланга [76] в области проектирования и эксплуатации телефонных станций. Общая схема СМО показана на рис.1.
Входной Правило Правило Каналы Выходной поток постановки Очередь обслуживания обслуживания поток требований в очередь требований Рисунок 1. Общая схема СМО. Требование на обслуживание (например, неисправный автомобиль, судно) поступает в обслуживающую систему (автомастерскую, порт). Если есть свободные каналы обслуживания (мастера, причалы), то требование выполняется. Если все каналы заняты, то требование ставится в очередь по определенным правилам или покидает систему не обслуженным. Основная задача теории массового обслуживания сводится к определению оптимального соотношения между входным потоком требований и числом обслуживающих каналов, при котором общие суммарные затраты минимальны. Общие суммарные затраты складываются из затрат обслуживания и затрат ожидания, причем по мере увеличения сервиса затраты обслуживания увеличиваются, а затраты ожидания уменьшаются. СМО можно описать, задавая следующие ее компоненты: · входной поток требований, · дисциплину очереди, · механизм обслуживания. Входной поток требований характеризуется вероятностным законом распределения моментов поступления требований в систему и количеством требований в каждом поступлении. В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач теории очередей, в которых поток требований является простейшим (пуассоновским). Простейший поток событий обладает тремя свойствами: 1. стационарностью – постоянным количеством событий в единицу времени;
2. отсутствием последействия – независимостью количества событий после любого момента времени от количества событий до него; 3. ординарностью – практической невозможностью одновременного поступления нескольких требований. Для простейшего потока частота наступления событий подчиняется закону Пуассона, то есть вероятность того, что за время t произойдет k событий, определяется:
где Вероятность того, что один причал занят (k=1) при отказе в среднем в единицу времени двух причалов (
Вероятность того, что все причалы свободны – 13%; вероятность того, что один причал занят – 27%; два – 27%; три – 18%; четыре – 9% и т.д. По теореме сложения вероятностей, вероятность суммы независимых событий равна сумме вероятностей этих событий, отсюда вероятность отказа в единицу времени не более четырех причалов равна сумме вероятностей отсутствия отказа и вероятностей отказа одной, двух, трех, четырех причалов:
Вероятность отказа более четырех причалов:
Дисциплина очереди описывает порядок обслуживания требований в системе. Длина очереди может быть ограниченной или неограниченной. Правила постановки в очередь: · FIFO – «первым пришел первым обслуживаешься», · LIFO – «последним пришел первым обслуживаешься», по другим приоритетам или случайно. Механизм обслуживания характеризуется продолжительностью процедур обслуживания и количеством одновременно обслуживаемых требований. Время обслуживания требований в системе является случайной величиной и обычно описывается э кспоненциальным законом распределения, то есть распределение длительности оставшейся части работ по обслуживанию не зависит от того, сколько оно уже продолжалось. Вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой:
где Введем в рассмотрение параметр
где Тобс – среднее время обслуживания одним каналом одного требования. Заметим, что, если Различают следующие виды СМО. В зависимости от условий ожидания требованием начала обслуживания различают СМО с отказами и с ожиданием. В системах с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и утрачиваются. В системах с ожиданием требование, застав все обслуживающие каналы занятыми, ставится на очередь вплоть до освобождения любого из каналов: · СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ожиданием и ограниченной длиной очереди. · СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания. · СМО, допускающие очередь, но с ограниченным числом циркулирующих в системе требований, называются системами с ограниченным потоком требований. По числу каналов обслуживания различают одноканальные и многоканальные системы. По числу фаз обслуживания – однофазные и многофазные (последовательная обработка требований на нескольких каналах). Определение оптимального числа причалов. Постановка задачи. Предполагается строительство нового порта (либо расширение действующего порта и т.п.). Требуется определить оптимальное число причалов. Исходными данными для решения задачи служат: · годовой грузооборот Q, · средняя грузоподъемность приходящих судов · среднее время обслуживания одного судна · годовые строительно-эксплуатационные расходы для одного причала · средняя себестоимость содержания судна в сутки на стоянке Предполагается, что входящий поток судов и поток обслуживания – простейшие. Общая схема решения задачи такова: 1. Определяется минимальное число причалов, при котором β<1 (многоканальная СМО с неограниченным ожиданием) – это условие существования установившегося режима. 2. Для полученного минимального числа причалов рассчитываются необходимые показатели: · вероятность того, что система (порт) свободна · средняя длина очереди · среднее время ожидания в очереди 3. Критерием оптимальности примем минимум комплексных приведенных затрат: расходы порта на строительство и эксплуатацию причалов, расходы судов в ожидании причала. 4. Рассчитываем время ожидания за год, комплексные приведенные годовые расходы за год. 5. Увеличиваем число причалов на единицу и повторяем предыдущий расчет. Если комплексные приведенные расходы уменьшились, то добавляем еще один причал, выполняем предыдущие расчеты. Процесс добавления причалов продолжается до тех пор, пока расходы не возрастут. Как только они станут больше, чем при предыдущем числе причалов, расчеты заканчиваются. Оптимальным числом причалов будет то, которое обеспечит минимальные расходы. Рассмотрим решение данной задачи на конкретном примере.
Исходные данные: · годовой грузооборот Q=2280 тыс. т, · средняя грузоподъемность приходящих судов · среднее время обслуживания одного судна · годовые строительно-эксплуатационные расходы для одного причала
· средняя себестоимость содержания судна в сутки на стоянке
Определить оптимальное число причалов в порту. Решение. Интенсивность входящего потока судов:
Интенсивность потока обслуживания:
Рассчитаем приведенную интенсивность потока заявок (среднее количество судов, прибывающих в порт за время обслуживания одного судна):
Имеем систему с неограниченным ожиданием. Это будет многоканальная система, так как Для многоканальной СМО с неограниченным ожиданием должно выполняться условие:
чтобы в системе был установившийся режим, и очередь не росла бесконечно. Из (14) найдем минимальное число причалов, при котором
Рассчитаем для n=4 показатели: · вероятность того, что все причалы свободны:
· среднюю длину очереди:
· среднее время ожидания в очереди:
Рассчитаем расходы флота в ожидании причала за год. В одном судозаходе каждое судно будет ожидать причал в среднем 5,22 сут., а за год ожидание за все судозаходы
где
Расходы флота
Расходы по причалам
Комплексные приведенные годовые расходы (по флоту и по порту) составят:
Добавим один причал, то есть примем n=5 и повторим предыдущие расчеты. Если общие годовые расходы увеличатся, то оптимальным числом причалов будет n=4. Если при n=5 расходы снизятся, то добавляем еще один причал и повторяем расчеты. Процесс добавления причалов продолжаем до тех пор, пока комплексные приведенные годовые расходы не станут расти. Число причалов, при котором эти расходы минимальны, будет оптимальным. Сведем результаты расчетов в табл.6. Как следует из табл.6, при n=7 комплексные приведенные расходы возросли; минимальные комплексные приведенные расходы соответствуют числу причалов, равному шести. Это и будет оптимальное число причалов. Таблица 6. Показатели обслуживания и расходы.
В рассмотренной задаче в качестве критерия оптимальности могут быть использованы и другие показатели, например, можно задаться допустимым средним временем ожидания причала; можно задаться соотношением среднего времени пребывания заявки в очереди и доли времени простоя обслуживающих каналов, и другие.
Вопросы по теме 9: 1. Какие основные типы зависимостей исходов от альтернатив Вы знаете? 2. Что называется игрой? Как составляется платежная матрица? 3. Какова цель теории игр? Как определяется цена игры? 4. Что называют чистой ценой игры или седловой точкой? 5. Как рассчитывают показатель риска? 6. Запишите расчетные формулы для критерия, основанного на известных вероятностных состояниях «природы». 7. Запишите расчетные формулы для критериев Вальда, Гурвица и Сэвиджа. 8. Перечислите области применения СМО. 9. Охарактеризуйте поток заявок в систему. 10. По какому закону распределено поступление заявок в СМО? 11. По какому закону распределено время обслуживания одной заявки в СМО? 12. Название и физический смысл 13. Название и физический смысл 14. Приведите классификацию СМО. 15. В каком случае говорят о СМО с отказом? 16. В каком случае говорят о СМО с ожиданием? 17. Какие классы СМО с ожиданием Вы знаете? 18. Что служит исходными данными для решения задачи определения оптимального числа причалов? Общая схема решения задачи. 19. Как определяется минимальное число причалов? 20. Как рассчитывается интенсивность входящего потока? 21. Какие показатели обслуживания рассчитываются в задаче определения оптимального числа причалов? 22. Какие критерии оптимальности могут быть использованы при решении задачи определения оптимального числа причалов?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.144.32 (0.078 с.) |













 (11)
(11) - количество событий в единицу времени или среднее число требований, поступающих в единицу времени (интенсивность потока).
- количество событий в единицу времени или среднее число требований, поступающих в единицу времени (интенсивность потока).
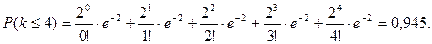

 (12)
(12)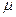 - среднее число требований, удовлетворяемых в единицу времени; величина, обратная среднему времени обслуживания.
- среднее число требований, удовлетворяемых в единицу времени; величина, обратная среднему времени обслуживания. - коэффициент загрузки системы или среднее число каналов (причалов), которые необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования (суда):
- коэффициент загрузки системы или среднее число каналов (причалов), которые необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования (суда): (13)
(13)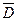 ,
, ,
, ,
,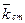 .
. ;
; ;
; .
. суд./сут.
суд./сут.
 (суд.).
(суд.). >1.
>1. (14)
(14)


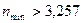 . Принимаем
. Принимаем 


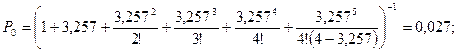
 ;
; судна;
судна; (сут.).
(сут.). составит:
составит:
 - число судозаходов в год.
- число судозаходов в год. судо-сут.
судо-сут.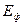 составят:
составят: тыс. долл.
тыс. долл. будут такими:
будут такими: тыс. долл.
тыс. долл. тыс. долл.
тыс. долл.
 , судов
, судов
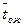 , сут.
, сут.



