Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многокритериальная (векторная) оптимизация.
Когда есть ряд целей, которые не могут быть отражены одним критерием, возникают задачи многокритериальной (векторной) оптимизации. В зависимости от источника многокритериальности задачи могут быть разделены на несколько классов: · задачи оптимизации на множестве целей; · задачи оптимизации на множестве объектов; · задача оптимизации на множестве условий функционирования; · задачи оптимизации на множестве этапов функционирования. При решении задач векторной оптимизации возникает ряд проблем, которые носят не вычислительный, а концептуальный характер. Главная из них – выбор принципа оптимальности, что дает ответ на вопрос: в каком смысле оптимальное решение лучше других? В задачах векторной оптимизации имеется противоречие между некоторыми критериями. Через это область допустимых решений распадается на две части, которые не пересекаются: область согласия и область компромисса. В области согласия противоречия между критериями нет, и качество решения может быть улучшено одновременно по всем критериям, без ухудшения какого-либо из них. В области компромисса является противоречие между некоторыми критериями: улучшение качества по одним критериям ухудшает качество решения по другим. Очевидно, что оптимальное решение может принадлежать только области компромисса, так как в области согласия решение может и должно быть улучшено. Решение задачи векторной оптимизации обычно сводят к решению одной или последовательности однокритериальных задач. Задачи векторной оптимизации можно решить несколькими методами: · оптимизацией обобщенного скалярного критерия (методом свертки критериев), · оптимизацией главного локального критерия, · методом последовательных уступок. Одним из основных подходов к решению многокритериальных задач заключается в свертывании локальных критериев в один критерий, который называют обобщенным. Он обычно имеет вид взвешенной суммы локальных критериев оптимальности:
где λk ( Весовые коэффициенты λk ( λk ≥ 0( Более важным критериям присваивается больший весовой коэффициент.
Объединение нескольких показателей в один основано на неявном допущении, что недостаток в одном показателе может быть компенсирован за счет другого. При использовании метода свертки критериев возникает две проблемы: 1. Как поступить, если локальные критерии имеют разные единицы измерения? 2. Как рассчитать весовые коэффициенты критериев? Рассмотрим: как решаются эти проблемы. Для решения первой проблемы воспользуемся методом нормализации локальных критериев. Под нормализацией понимают приведение локальных критериев к единому, как правило, безразмерному виду. При использовании нормализации вместо натурального критерия вводится его отношение к некоторой нормализующей величине, измеряемой в тех же единицах, что и сам критерий. В результате этого все локальные критерии становятся безразмерными. Нормирование не может производиться путем деления значения частного критерия на произвольную величину, имеющую ту же размерность. Нормирующий делитель должен иметь хорошо обоснованную логическую базу. Рассмотрим способ нормализации к разности между максимальным и минимальным значениями локального критерия. Здесь предварительно нужно решить 2s однокритериальных задач для нахождения Нормализованная локальная целевая функция будет иметь вид: · для минимизируемых критериев
· для максимизируемых критериев
Нормализованная обобщенная целевая функция может иметь вид:
Замечание: если в задаче часть локальных критериев максимизируется, а часть минимизируется, то до нормализации все критерии нужно привести к единому виду (все на максимум либо все на минимум). Чтобы преобразовать задачу на минимум в задачу на максимум, нужно изменить знаки коэффициентов при неизвестных в ЦФ на противоположные. Весовые коэффициенты локальных критериев чаще всего определяются на основе экспертных оценок. В методе свертки критериев используется такой принцип оптимальности: оптимальным планом задачи векторной оптимизации считается план, при котором обобщенная ЦФ достигает искомого экстремума. Объединение локальных критериев в обобщенный критерий хотя и дает представление о сравнительных качествах планов по совокупности показателей, но имеет существенные недостатки. Главными из них являются:
· слабая связь весовых коэффициентов с их действительной ролью; · трудности в установлении объективных значений весовых коэффициентов λk ( · компенсация малой величины одного критерия большим значением другого. Несмотря на слабые стороны метода свертки критериев, он позволяет в ряде случаев решить многокритериальную задачу и получить полезные результаты. Если среди локальных критериев можно выделить главный, то тогда для решения задач векторной оптимизации применяют оптимизацию главного локального критерия. В этом случае задачу векторной оптимизации сводят к однокритериальной задаче, в которой главный критерий выступает в качестве ЦФ, а все остальные локальные критерии записываются как ограничения, причем на них накладывается требование: их значения должны быть не менее заданных допустимых уровней. При применении метода выделения главного локального критерия используется следующий принцип оптимальности: оптимальным планом многокритериальной задачи считается тот, при котором главный локальный критерий достигает экстремума, при условии, что другие локальные критерии принимают значения не хуже заданных условий. Метод последовательных уступок может быть применен в случае, когда локальные критерии можно расположить в порядке убывания их важности (ранжировать). Оптимальным планом считается план, полученный при поиске условного максимума последнего по важности критерия. Метод выделения главного локального критерия и метод последовательных уступок подробно рассмотрены в научной литературе. Рассмотрим постановку и экономико-математическую модель многокритериальной транспортной задачи. Решается задача выбора маршрута доставки контейнерных грузов от отправителя до потребителя в смешанном сообщении с выбором вида транспорта. В m пунктах имеется однородный груз (контейнеры), который необходимо доставить n получателям. Доставка контейнеров осуществляется в смешанном сообщении – морская часть пути и наземная – железнодорожным или автомобильным видом транспорта. Перегрузка контейнеров может быть осуществлено в Г портах. Известна стоимость доставки 1 контейнера (TEU) от каждого иностранного порта до порта перевалки в Украине, а также от каждого порта перевалки получателям каждым видом транспорта. Необходимо выбрать маршрут доставки груза от отправителей до получателей, обеспечивающий минимальные затраты, а также минимальное время доставки. Введем обозначения: i – порт отправления контейнеров,
j – пункт назначения, p – вид транспорту, d – контейнерная линия, которой осуществляются перевозки, ai – количество контейнеров в порту отправления i, TEU; bj – потребность в контейнерах в пунктах назначения j, TEU;
где Tiγd – время доставки контейнеров из i -го порта отправления до порта перевалки γ контейнерной линией d, сутки;
Qi – количество контейнеров, вывезенных из i -го порта отправления, TEU;
где Tγjр – время доставки контейнеров из γ порта перевалки до j -го пункта назначения р -м видом транспорта, сутки; Qj – количество контейнеров, ввезенных в j -ый пункт назначения, TEU. Введем 2 группы переменных:
Экономико-математическая модель задачи векторной оптимизации (для импортного варианта) имеет вид:
ЦФ (38) отображает затраты на доставку контейнеров на всем маршруте. ЦФ (39) отображает время на доставку контейнеров на всем маршрут. (40) – ограничения о вывозе всех контейнеров из портов отправления. (41) – ограничения по удовлетворению потребностей получателей. (42) – балансовые уравнения, смысл которых состоит в том, что количество контейнеров, поступивших в порт перевалки (левая часть), должно быть полностью из него отправлено (правая часть). Для экспортного варианта экономико-математическая модель имеет вид:
В этой модели все переменные имеют такое же значение, как и в предыдущей, а также:
Для решения многокритериальной транспортной задачи, например, методом свертки критериев используется MS Excel процедура «Поиск решения», которая находится в меню «Сервис». Вопросы по теме 7: 1. Для решения каких экономических задач может быть использован аппарат ЛП? 2. Запишите экономико-математическую модель общей задачи ЛП. 3. В чем отличие стандартной задачи ЛП от канонической? 4. Что называют допустимым, оптимальным решениями задачи ЛП? 5. Сформулируйте постановку задачи определения оптимальной структуры флота судоходной компании. Какой критерий оптимальности используется? Что является параметрами управления? Запишите математическую модель задачи. 6. Что понимается под структурой флота? 7. Сколько групп ограничений в задаче определения оптимальной структуры флота судоходной компании? 8. Сформулируйте постановку задачи выбора вида транспорта для доставки груза. Какой критерий оптимальности используется? Что является параметрами управления? Запишите математическую модель задачи. 9. Как учитываются провозные способности видов транспорта в математической модели? Запишите ограничения. 10. Как учитываются перевозки разнородных грузов? Запишите модель. 11. Сформулируйте постановку задачи выбора маршрута доставки грузов. 12. Запишите математическую модель задачи выбора маршрута доставки грузов. Какой критерий оптимальности используется? Что является параметрами управления? 13. Перечислите основные классы задач векторной оптимизации. 14. Какие задачи называются многокритериальными, или задачами векторной оптимизации? 15. Перечислите основные методы решения многокритериальных задач. 16. Для чего и как выполняется нормализация критериев? 17. Как определяются весовые коэффициенты локальных критериев? 18. Что характеризуют весовые коэффициенты критериев? 19. Какой принцип оптимальности используется в методе свертки критериев? 20. Какой принцип оптимальности используется в методе выделения главного локального критерия? 21. Раскройте идею метода последовательных уступок? Тема 8. Математические методы планирования: нелинейное программирование. Основные понятия и математическая модель задачи. Графический способ. Задачи линейного программирования были первыми подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 г. Ж. Фурье [72] и затем в 1947 г. Дж. Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции - симплекс-метод, ставший основным при решении задач линейного программирования. Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 30-м годам ХХ столетия. Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны.
В 1951 г. была опубликована работа Куна [73] и Таккера [74], в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области. Имеются проблемы, в которых связи заведомо не являются линейными. Источники нелинейности относятся в основном к одной из двух категорий: 1) реально существующие и эмпирически наблюдаемые нелинейные соотношения, например: непропорциональные зависимости между объемом производства и затратами; между количеством используемого в производстве компонента и некоторыми показателями качества готовой продукции; между затратами сырья и физическими параметрами (давление, температура и т.п.) соответствующего производственного процесса; между выручкой и объемом реализации и др.; 2) установленные (постулируемые) руководством правила поведения или задаваемые зависимости, например: формулы или правила расчета с потребителями энергии или других видов услуг; эвристические правила определения страховых уровней запаса продукции; гипотезы о характере вероятностного распределения рассматриваемых в модели случайных величин; различного рода договорные условия взаимодействия между партнерами по бизнесу и др. Таковы, например, задачи увеличения масштабов производства, перехода на новую технологию, оптовой торговли и т.д. Поэтому ясна необходимость изучения нелинейных моделей и методов их анализа. Модели эти, конечно, сложнее линейных и разработанные для них методы менее эффективны, чем методы решения линейных задач. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ (НЛП) - раздел математического программирования, посвященный теории и методам решения задач оптимизации нелинейных функций на множествах, задаваемых нелинейными ограничениями (равенствами и неравенствами). В общем виде задача НЛП описывается с помощью следующей модели нелинейного программирования:
где х = (x1, х2,..., хn) - вектор переменных задачи. Задача (1) - (3) называется задачей нелинейного программирования в стандартной форме на максимум. Может быть сформулирована также задача НЛП на минимум. Вектор х = (x1, х2,..., хn), компоненты хj которого удовлетворяют ограничениям (2) и (3), называется допустимым решением или допустимым планом задачи НЛП. Совокупность всех допустимых планов называется множеством допустимых планов. Допустимое решение задачи НЛП, при котором целевая функция (1) достигает максимального значения, называется оптимальным решением задачи НЛП. В отличие от задач линейного программирования, любая из которых может быть решена симплекс-методом, не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Какой-то алгоритм может оказаться чрезвычайно эффективным для решения задач одного типа и неудачным для задач другого типа. Для решения задачи нелинейного программирования было предложено много методов, которые можно классифицировать по различным признакам: 1. По количеству локальных критериев в целевой функции методы НЛП делятся на: · однокритериальные, · многокритериальные. 2. По длине вектора методы делятся на: · однопараметрические или одномерные (n=1), · многопараметрические или многомерные (n>1). 3. По наличию ограничений методы НЛП делятся на: · без ограничений (безусловная оптимизация), · с ограничениями (условная оптимизация). 4. По типу информации, используемой в алгоритме поиска экстремума, методы делятся на: · методы прямого поиска, т.е. методы, в которых при поиске экстремума целевой функции используются только ее значения; · градиентные методы первого порядка, в которых при поиске экстремума функции используются значения ее первых производных; · градиентные методы второго порядка, в которых при поиске экстремума функции наряду с первыми производными используются и вторые производные. Ни один метод нелинейного программирования не является универсальным. В каждом конкретном случае необходимо приспосабливать применяемый метод к особенностям решаемой задачи. Эффективность алгоритма может даже существенно зависеть от постановки задачи, например, от изменения масштабов измерения тех или иных переменных. Поэтому алгоритмы разрабатываются для каждого класса (типа) задач. Программы, ориентированные на решение определенного класса задач, как правило, не гарантируют правильность решения любых задач данного класса, и оптимальность решения рекомендуется проверять в каждом конкретном случае. Основная трудность решения задач НЛП состоит в том, что эти задачи являются многоэкстремальными, и известные численные методы их решения гарантируют в общем случае сходимость минимизирующих последовательностей лишь к точкам локальных экстремумов. Наличие локальных экстремумов затрудняет решение задач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найденный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять локальный экстремум, который может существенно отличаться от глобального. В течение последних двух десятилетий из нелинейного программирования выделились самостоятельные разделы: · выпуклое программирование, · квадратичное программирование, · целочисленное программирование, · стохастическое программирование, · динамическое программирование и др. Задачи выпуклого программирования – это задачи, в которых определяется минимум выпуклой функции (или максимум вогнутой), заданной на выпуклом замкнутом множестве. Эти задачи среди задач нелинейного программирования наиболее изучены. Среди задач выпуклого программирования более подробно изучены задачи квадратичного программирования. В этих задачах целевая функция – квадратична, а ограничения – линейны. В задачах целочисленного программирования неизвестные параметры могут принимать только целочисленные значения. В задачах стохастического программирования в целевой функции или в функциях ограничений содержатся случайные величины, которые подчиняются законам теории вероятностей. В задачах динамического программирования ограничения содержат как параметр время и при этом описываются дифференциальными уравнениями. Процесс нахождения решений в задачах динамического программирования является многоэтапным. Важный признак систематизации – классификация моделей по ее элементам: 1) исходным данным, 2) искомым переменным, 3) зависимостям, описывающим цели задачи (моделирования) и ограничения. Сочетание различных элементов модели приводит к различным классам задач оптимизации, которые требуют разных методов решения, следовательно, и разных программных средств. Таблица 1. Классификация моделей по ее элементам.
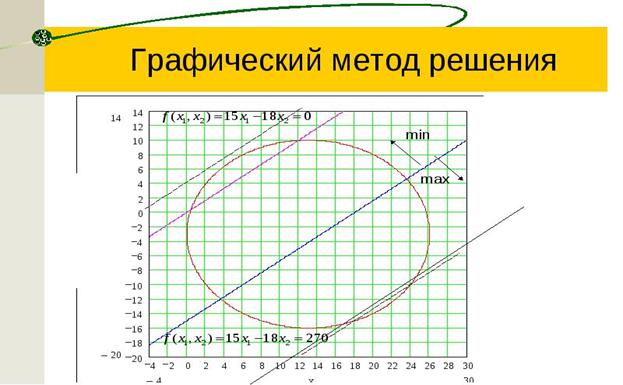
Графический метод нелинейного программирования Задачи НЛП обладают свойствами, которые усложняют процесс их решения по сравнению с задачами линейного программирования: 1. Множество допустимых планов (мы будем обозначать его буквой G) может иметь очень сложную структуру. Например, быть невыпуклым или несвязным. 2. Глобальный максимум (минимум) может достигаться как внутри множества G, так и на его границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов). 3. Целевая функция f(x) может быть не дифференцируемой, что затрудняет применение классических методов математического анализа. В силу названных факторов задачи нелинейного программирования настолько разнообразны, что для них, как уже упоминалось ранее, не существует общего метода решения. Рассмотрим графический метод решения задач НЛП. Его алгоритм такой же, как и для решения задач линейного программирования. Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно. Если количество переменных в неравенствах, задающих область допустимых планов задач, равно 2, то ее можно изобразить на координатной плоскости. Каждое неравенство определяет некоторую полуплоскость. Пересечение данных полуплоскостей G является областью допустимых планов задач. Поведение целевой функции в рамках двумерной иллюстрации может быть охарактеризовано с помощью линии уровня. Линией уровня функции называется множество точек из области ее определения, в которых функция принимает одно и тоже фиксированное значение. Градиент функции - это вектор, указывающий направление наиболее быстрого возрастания функции. Чтобы найти оптимальное решение задачи НЛП, нужно выполнить следующие действия: 1. Найти область допустимых решений (ОДР), определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения. 2. Построить семейство линий уровня функции при различных значениях числового параметра Z. 3. При решении задачи на минимум определить направление убывания, а для задачи на максимум - направление возрастания линий уровня ЦФ. 4. Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра Z. Эта точка будет оптимальным решением. Если ЦФ не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения. 5. Найти координаты точки оптимума и определить в ней значение ЦФ. Отметим, что в отличие от задачи ЛП точка оптимума в задаче НЛП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества. Возможен и случай касания линии уровня грани (линии) множества G, соответственно, все точки, лежащие на этой грани, будут являться альтернативными оптимальными планами. Заметим, что аналогичным образом могут быть построены интерпретации задач нелинейного программирования для случая трехмерного пространства R3, где множеству G будет соответствовать некоторый ограниченный или неограниченный многогранник, а поведение целевой функции будет характеризоваться поверхностями (плоскостями) уровня. Этот метод может быть применен не только к задачам с двумя или тремя переменными и ограничениями в виде неравенств, но и к задачам, у которых i - k =2 (i - количество ограничений, k - количество неизвестных). Действительно, можно выбрать две произвольные переменные и, используя систему уравнений (неравенств), выразить через них остальные переменные. Рассмотрим примеры решения задач НЛП графическим методом. Задача №1. Решить следующий пример графическим методом:
Решение. Область допустимых решений – окружность с центром в точке х1=13, х2=-3 и радиусом = 13. Ответ:
Задача №2. На предприятии имеется два вида ресурсов. Определите оптимальное распределение величин затрачиваемых ресурсов на производство некоторого продукта, если цена ресурса первого вида 3 единицы, второго – 4 единицы, а всего на производство выделено 24 единицы. Известно, что из количества х первого ресурса и у второго ресурса можно получить Решение. Пусть х - количество ресурсов первого вида, у - количество ресурсов второго вида. Математическая модель задачи: на множестве ограничений
Если целевой функции придавать фиксированные значения 1, 2, 3,..., то будем получать окружности с центром в начале координат и радиусом 1, 2, 3,… Начертим ряд окружностей (линии уровня целевой функции). Из рисунка будет видно, что функция z = Значит, количество первого ресурса должно равняться 8, а использование второго ресурса нерационально.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 3017; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.216.163 (0.135 с.) |
 → min (max), (31)
→ min (max), (31)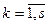 ) – весовые коэффициенты, выражающие степень важности каждого локального критерия.
) – весовые коэффициенты, выражающие степень важности каждого локального критерия.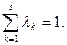 (32)
(32) и
и 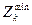 (
(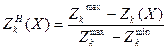 (
( (
( λk • ZHk(X) → min (max) (35)
λk • ZHk(X) → min (max) (35)
 - порт перевалки,
- порт перевалки, 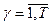 ;
; ;
;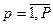 ;
;
 - стоимость доставки одного контейнера из i -ого порта отправления до порта перевалки
- стоимость доставки одного контейнера из i -ого порта отправления до порта перевалки  - время доставки одного контейнера из i -ого порта отправления до порта перевалки
- время доставки одного контейнера из i -ого порта отправления до порта перевалки 
 , (36)
, (36) - стоимость доставки одного контейнера из
- стоимость доставки одного контейнера из  - время доставки одного контейнера из
- время доставки одного контейнера из 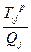 , (37)
, (37)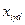 - количество контейнеров, которое может быть доставлено из i -ого порта отправления до порта перевалки
- количество контейнеров, которое может быть доставлено из i -ого порта отправления до порта перевалки  - количество контейнеров, которое может быть доставлено из
- количество контейнеров, которое может быть доставлено из  (38)
(38) (39)
(39) , (40)
, (40) , (41)
, (41)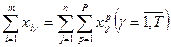 , (42)
, (42) Є N, N - множество целых чисел (43)
Є N, N - множество целых чисел (43)
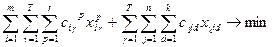 (44)
(44)
 (45)
(45) ai,
ai,  (46)
(46) = bj,
= bj,  (47)
(47) =
= 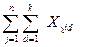
 (48)
(48)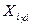 ≥ 0
≥ 0 
 ,
,  ≥ 0
≥ 0 
 ,
,  - количество контейнеров, которое может быть доставлено из пункта отправления i до порта перевалки γ наземным видом транспорту р, TEU;
- количество контейнеров, которое может быть доставлено из пункта отправления i до порта перевалки γ наземным видом транспорту р, TEU; - количество контейнеров, которое может быть доставлено из порта перевалки γ до порта назначения j контейнерной линией d, TEU;
- количество контейнеров, которое может быть доставлено из порта перевалки γ до порта назначения j контейнерной линией d, TEU;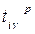 - время доставки одного контейнера от i -ого пункта отправления до порта перевалки
- время доставки одного контейнера от i -ого пункта отправления до порта перевалки 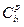 - стоимость доставки одного контейнера от i -ого пункта отправления до порта перевалки
- стоимость доставки одного контейнера от i -ого пункта отправления до порта перевалки  - время доставки одного контейнера от порта перевалки γ до порта назначения j контейнерной линией d, сутки/ TEU;
- время доставки одного контейнера от порта перевалки γ до порта назначения j контейнерной линией d, сутки/ TEU; - стоимость доставки одного контейнера от порта перевалки γ до порта назначения j контейнерной линией d, долл./ TEU.
- стоимость доставки одного контейнера от порта перевалки γ до порта назначения j контейнерной линией d, долл./ TEU. (1)
(1)
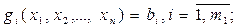 (2)
(2)

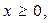 (3)
(3)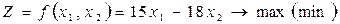
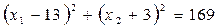
 ;
;  .
.
 единиц продукта.
единиц продукта.