
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена переменных в двойном интеграле.
Пусть функция
где В частности, при переходе к полярной системе координат на плоскости
Пример 19. Вычислим интеграл W = Поскольку границей области интегрирования является окружность
= =
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ
Пусть
(криволинейного цилиндра), ограни- ченного поверхностью плоскостью ческой поверхностью, вырезающей на
V =
Площадь S квадрируемой области Рис.9. D на плоскости xOy выражается формулой
Площадь F гладкой поверхности
по формуле
В последней формуле D - проекция данной Поверхности на плоскость xOy (рис.10). Рис. 10. Аналогичные формулы имеют место, если гладкая поверхность задана уравнением F1 =
Пример 20. Найдем объем тела, ограниченного поверхностью Заметим, что уравнение
параллельными оси x, а плоскость
(рис. 11). Область D ограничена прямыми
x Рис. 11 Объем тела V = = =20/3 (куб.ед.).
Пример 21. Найдем объем тела, ограниченного плоскостями
вычислить, изображено на рис. 12. Объем тела вычисляется по формуле V =
вычислен в примере 19, он равен 3p,
3p (куб.ед.). y
Пример 22. Найдем площадь x фигуры D, ограниченной кривой Рис. 12
Заметим, что кривая симметрична относительно оси x (уравнение кривой не меняется при замене y на - y), расположена в правой полуплоскости (левая часть уравнения неотрицательна, поэтому и правая часть должна быть неотрицательной). Кривая пересекает ось x в точках Кроме того, она ограничена: из очевидного неравенства Для вычисления площади фигуры D, ограниченной данной кривой,
Наличие в формуле кривой двучлена
Полярное уравнение кривой: Из условия от -p/2 до p/2, при каждом фиксированном Рис. 13 q переменная r изменяется от 0 до S= =
Пример 23. Вычислим площадь части параболоида Очевидно, что указанная часть поверхности состоит из четырех равных между собой частей (в силу симметрии параболоида и цилиндра). Поэтому мы можем вычислять площадь одной четвертой части указанной поверхности (например, той, которая находится в первом октанте) и результат умножить на четыре. Таким образом, F= Областью интегрирования является часть круга, а подынтегральная функция содержит в себе выражение F = =
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Пусть L - простая спрямляемая незамкнутая кривая, заданная параметрически: Напомним, что L называется простой незамкнутой кривой, если функции
Пусть на кривой L заданы две функции Введем обозначения:
Если существует конечный предел
Замечания. 1. Из определения криволинейного интеграла следует, что при изменении направления обхода кривой L изменяется и знак интеграла, т.е.
2.Если кривая L замкнутая (т.е. точка A Интеграл по замкнутому контуру в положительном направлении обозначают так:
3. Криволинейные интегралы обладают свойствами линейности и аддитивности.
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.150.89 (0.159 с.) |
 непрерывна на замкнутом квадрируемом множестве D, функции
непрерывна на замкнутом квадрируемом множестве D, функции 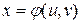 ,
,  непрерывны вместе со своими частными производными первого порядка в замкнутом квадрируемом множестве Q и задают взаимно однозначное отображение множества Q на множество D. Тогда имеет место следующая формула замены переменных в двойном интеграле
непрерывны вместе со своими частными производными первого порядка в замкнутом квадрируемом множестве Q и задают взаимно однозначное отображение множества Q на множество D. Тогда имеет место следующая формула замены переменных в двойном интеграле
 ,
, . Этот определитель называется якобианом отображения
. Этот определитель называется якобианом отображения  ,
,  якобиан вычисляется следующим образом:
якобиан вычисляется следующим образом:  , поэтому
, поэтому  .
. , где D - круг
, где D - круг  .
. , то при вычислении данного интеграла удобно перейти к полярным координатам
, то при вычислении данного интеграла удобно перейти к полярным координатам  (уравнение окружности в полярной системе координат имеет вид
(уравнение окружности в полярной системе координат имеет вид  ,
,  ). Используя формулу замены переменных, получим: W
). Используя формулу замены переменных, получим: W 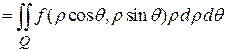 =
=
 =
= =
=  .
. непрерывная и неотрицательная функция, определенная на замкнутом квадрируемом множестве D.
непрерывная и неотрицательная функция, определенная на замкнутом квадрируемом множестве D. Объем цилиндрического тела
Объем цилиндрического тела и прямой цилиндри-
и прямой цилиндри- плоскости
плоскости  вычисляется по формуле:
вычисляется по формуле: S =
S =  .
. , вычисляется
, вычисляется
 F =
F = 
 ,
,  , (или уравнением
, (или уравнением  ,
,  ):
): (или F2 =
(или F2 = 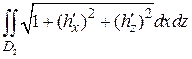 ).
). и плоскостями
и плоскостями  ,
,  ,
,  .
. z поверхность с образующими,
z поверхность с образующими,
 y быть задана неравенствами
y быть задана неравенствами  ,
, .
. =
=


 ,
,  Тело, объем которого требуется z
Тело, объем которого требуется z
 поэтому искомый объем равен
поэтому искомый объем равен (
(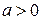 ).
). .
. следует, что
следует, что  , а поскольку
, а поскольку  , то
, то  . Эскиз кривой дан на рис. 13.
. Эскиз кривой дан на рис. 13. воспользуемся формулой S =
воспользуемся формулой S =  подсказывает, что целесообразно
подсказывает, что целесообразно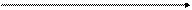 перейти к полярным координатам
перейти к полярным координатам .
. следует, что q меняется
следует, что q меняется . Используя симметричность D, мы можем вычислить площадь фигуры, расположенной в первой четверти и удвоить ее. Таким образом,
. Используя симметричность D, мы можем вычислить площадь фигуры, расположенной в первой четверти и удвоить ее. Таким образом, =
= 
 =
= (кв. ед.).
(кв. ед.). , вырезанной цилиндром
, вырезанной цилиндром  , где D - четверть круга
, где D - четверть круга  , следовательно,
, следовательно,  ,
,  , и F =
, и F = 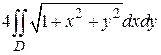 .
. ,
,  , следовательно,
, следовательно,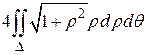 =
= 

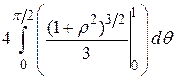 =
=  (кв. ед.).
(кв. ед.). ,
,  ,
,  .
. ,
,  непрерывны на
непрерывны на 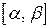 и различным значениям параметра t из отрезка
и различным значениям параметра t из отрезка  и
и 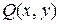 . Разобьем отрезок
. Разобьем отрезок  . При этом кривая L разбивается на n частей точками
. При этом кривая L разбивается на n частей точками 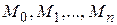 ;
;  - координаты точки
- координаты точки  .
. ,
,  ,
,  - длина дуги
- длина дуги  ,
,  . На каждой дуге
. На каждой дуге  и составим интегральную сумму
и составим интегральную сумму
 .
. , который не зависит ни от способа разбиения отрезка
, который не зависит ни от способа разбиения отрезка  .
.
 .
.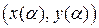 совпадает с точкой B
совпадает с точкой B  ), то для L можно указать два направления обхода от A к B. Если область, лежащая внутри контура, остается слева по отношению к движущейся по контуру точке, то такое направление обхода кривой L называется положительным, а противоположное ему - отрицательным.
), то для L можно указать два направления обхода от A к B. Если область, лежащая внутри контура, остается слева по отношению к движущейся по контуру точке, то такое направление обхода кривой L называется положительным, а противоположное ему - отрицательным. . Заметим, что в случае вычисления интеграла по замкнутому контуру в качестве начальной (и конечной) точки можно взять любую точку контура.
. Заметим, что в случае вычисления интеграла по замкнутому контуру в качестве начальной (и конечной) точки можно взять любую точку контура.


