
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения вероятностей
Теорема сложения вероятностей формулируется следующим образом. Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
Яндекс.ДиректВсе объявленияРешаем задачи и контрольные Теория вероятностей, мат. статистика, Статистика, Физика, Химия. Гарантия mathematic.by Элементы Яндекса в Firefox! Новое расширение для Firefox. Поиск и нужные сервисы всегда под рукой element.yandex.ru Элементы Яндекса в Firefox! Новое расширение для Firefox. Поиск и нужные сервисы всегда под рукой element.yandex.ru Докажем теорему сложения вероятностей для схемы случаев. Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек:
Предположим, что из этих случаев
Так как события
Подставляя полученные выражения в формулу (3.2.1), получим тождество. Теорема доказана. Обобщим теорему сложения на случай трех событий. Обозначая событие
Очевидно, методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Действительно, предположим, что она справедлива для n событий:
и докажем, что она будет справедлива для
Обозначим:
Имеем:
Но так как для n событий мы считаем теорему уже доказанной, то
откуда
что и требовалось доказать. Таким образом, теорема сложения вероятностей применима к любому числу несовместных событий. Её удобнее записать в виде:
Отметим следствия, вытекающие из теоремы сложения вероятностей. Следствие 1. Если события
Доказательство. Так как события
Так как
откуда
что и требовалось доказать. Перед тем как вывести второе следствие теоремы сложения, определим понятие о «противоположных событиях». Противоположными событиями называются два несовместных события, образующих полную группу. Событие, противоположное событию Примеры противоположных событий.
1) 2) 3) 4) Следствие 2. Сумма вероятностей противоположных событий равна единице:
Это следствие есть частный случай следствия 1. Оно выделено особо ввиду его большой важности в практическом применении теории вероятностей. На практике весьма часто оказывается легче вычислить вероятность противоположного события Рассмотрим несколько примеров на применение теоремы сложения и её следствий. Пример 1. В лотерее 1000 билетов; из них на один билет падает выигрыш 500 руб., на 100 билетов – выигрыши по 100 руб., на 50 билетов – выигрыши по 20 руб., на 100 билетов – выигрыши по 5 руб., остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 руб. Решение. Рассмотрим события:
Очевидно,
По теореме сложения вероятностей
Пример 2. Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны. Решение. Рассмотрим события:
Очевидно,
Так как при сбрасывании одной бомбы события
Пример 3. Круговая мишень (рис. 3.2.1) состоит из трех зон: I, II и III. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. Найти вероятность промаха.
Рис. 3.2.1. Решение. Обозначим
где
откуда
Как уже указывалось, теорема сложения вероятностей (3.2.1) справедлива только для несовместных событий. В случае, когда события
В справедливости формулы (3.2.3) можно наглядно убедиться, рассматривая рисунок 3.2.2.
Рис. 3.2.2. Аналогично вероятность суммы трех совместных событий вычисляется по формуле
Справедливость этой формулы также наглядно следует из геометрической интерпретации (рис. 3.2.3).
Рис. 3.2.3. Методом полной индукции можно доказать общую формулу для вероятности суммы любого числа совместных событий:
где суммы распространяются на различные значения индексов Формула (3.2.4) выражает вероятность суммы любого числа событий через вероятности произведений этих событий, взятых по одному, по два, по три и т.д. Аналогичную формулу можно написать для произведения событий. Действительно, из рис. 3.2.2 непосредственно ясно, что
Из рис. 3.2.3 видно, что
Общая формула, выражающая вероятность произведения произвольного числа событий через вероятности сумм этих событий, взятых по одному, по два, по три и т.д., имеет вид:
Формулы типа (3.2.4) и (3.2.7) находят практическое применение при преобразовании различных выражений, содержащих вероятности сумм и произведений событий. В зависимости от специфики задачи в некоторых случаях удобнее бывает пользоваться только суммами, а в других только произведениями событий: для преобразования одних в другие и служат подобные формулы. Пример. Техническое устройство состоит из трех агрегатов: двух агрегатов первого типа -
где Требуется выразить вероятность события Решение. По формуле (3.2.3) имеем:
по формуле (3.2.5)
по формуле (3.2.6)
Подставляя эти выражения в (3.2.8) и производя сокращения, получим:
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.108 (0.021 с.) |
 . (3.2.1)
. (3.2.1)
 благоприятны событию
благоприятны событию  , а
, а  – событию
– событию  . Тогда
. Тогда
 благоприятны
благоприятны 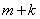 случаев и
случаев и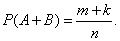
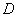 , и присоединяя к сумме еще одно событие
, и присоединяя к сумме еще одно событие  , легко доказать, что
, легко доказать, что

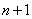 событий:
событий:

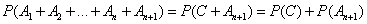 .
. ,
, ,
, . (3.2.2)
. (3.2.2)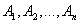 образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
образуют полную группу несовместных событий, то сумма их вероятностей равна единице: .
. .
. ,
, .
. - выпадение цифры при бросании монеты;
- выпадение цифры при бросании монеты; - отказ хотя бы одного элемента;
- отказ хотя бы одного элемента; - обнаружение не более одного бракованного изделия.
- обнаружение не более одного бракованного изделия. .
. и находят
и находят  .
. - выиграть 20 руб.,
- выиграть 20 руб., - выиграть 100 руб.,
- выиграть 100 руб., - выиграть 500 руб.
- выиграть 500 руб. .
. .
. несовместны, то
несовместны, то .
.
 ,
, - попадание соответственно в первую, вторую и третью зоны
- попадание соответственно в первую, вторую и третью зоны ,
, .
. . (3.2.3)
. (3.2.3)
 .
.
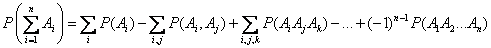 , (3.2.4)
, (3.2.4) , и т.д.
, и т.д. . (3.2.5)
. (3.2.5) . (3.2.6)
. (3.2.6) . (3.2.7)
. (3.2.7) ,
, ; (3.2.8)
; (3.2.8) ;
; .
.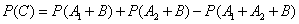 .
.


