Дискретные случайные величины и их характеристика. Закон распределения вероятностей дсв. Математическое ожидание дсв. Свойства математического ожидания.

Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.

Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.

Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y,Z,…), а их возможные значения — соответствующими малыми буквами (x_i, y_i,…).

Примеры: число очков, выпавших при броске игральной кости; число появлений герба при 10 бросках монеты; число выстрелов до первого попадания в цель; расстояние от центра мишени до пробоины при попадании.

Можно заметить, что множество возможных значений для перечисленных случайных величин имеет разный вид: для первых двух величин оно конечно (соответственно 6 и 11 значений), для третьей величины множество значений бесконечно и представляет собой множество натуральных чисел, а для четвертой — все точки отрезка, длина которого равна радиусу мишени. Таким образом, для первых трех величин множество значений из отдельных (дискретных), изолированных друг от друга значений, а для четвертой оно представляет собой непрерывную область. По этому показателю случайные величины подразделяются на две группы: дискретные и непрерывные.

БЮФФОНА ЗАДАЧА         об игле - классическая задача теории геометрических вероятностей, по праву считающаяся исходным пунктом развития этой теории. Впервые была отмечена Ж. Бюффоном в 1733 и воспроизведена вместе с решением в [1]. Ж. Бюффон рассматривал следующую ситуацию: на плоскость, разграфленную параллельными прямыми, отстоящими друг от друга на расстоянии а, наудачу бросается игла длиною . Какова вероятность того, что игла пересечет одну из проведенных параллелей? Очевидно, что положение иглы определяется расстоянием хот ее центра до ближайшей прямой линии и острым углом , составленным иглой с перпендикуляром к этой линии. Величина хлежит между нулем и - между нулем и . Предполагается, что точка распределена равномерно в соответствующем прямоугольнике (это равносильно тому, что случайные величины хи независимы и равномерно распределены на и ). Тогда искомая вероятность определяется как отношение площадей, соответствующих благоприятствующим и всем возможным исходам, и равна В свое время Б. з. послужила основой для экспериментальной проверки Бернулли теоремы. Действительно, если игла бросается праз и в тслучаях игла пересекает одну из линий, то частота при больших ппо теореме Бернулли должна быть близка к вероятности (*). Это соображение было использовано многими исследователями для определения числа я методом случайных испытаний (см. [1], [2]). Ж. Бюффон рассматривал и другие сходные задачи, в частности задачу о вероятности пересечения иглой линий, принадлежащих двум взаимно перпендикулярным системам, к-рые разбивают плоскость на прямоугольники со сторонами аи Ь, соответственно. Ответ Ж. Бюффона к этой задаче неверен. Правильный ответ: был указан П. Лапласом (РLaplace) в 1812. Лит.:[1] Buffon G., Essai d'arithmetique morale. Supplement a "1'Histoire Naturelle", v. 4 1777; [2] Usреnskу J. V., Introduction to mathematical Probability, N. Y.- L., 1937; [3] Кендалл М., Моран П., Геометрические вероятности, пер. с англ., М., 1972. А. В. Прохоров. BАЛЛЕ ПУССЕНА МЕТОД СУММИРОВАНИЯ- один из методов суммирования числовых рядов; обозначается символом (VP). Числовой ряд суммируется методом Балле Пуссена к числу S, если выполняется соотношение Метод предложен Ш. Балле Пуссеном [1]. Для ряда Фурье функции 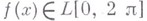средние Балле Пуссена (см. также Балле Пуссена сингулярный. интеграл).имеют вид - так наз. ядро Балле Пуссена. В. П. м. с. является регулярным методом суммирования. Этот метод сильнее всей совокупности Чезаро методов суммирования (см. Включение методов суммирования). Ввиду слабых аппроксимативных свойств В. Г1. м. с. практически не имеет применения в теории приближения функций.