
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечислительная комбинаторикаСтр 1 из 17Следующая ⇒
Случайное событие Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом Определение Математически случайное событие — подмножество пространства элементарных исходов случайного эксперимента; элемент алгебры или сигма-алгебры событий Пример Случайный эксперимент состоит в бросании игральной кости: пример случайного события — выпавшее число чётно; события «Выпала единица», «Выпала двойка» и т. д. — элементарные исходы эксперимента; совокупность всех событий «Выпала Комбинаторика Рассмотрим некоторое множество Х, состоящее из n элементов Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор
Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике). Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов. Примеры комбинаторных конфигураций и задач Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:
Примерами комбинаторных задач являются:
Ответ: 52! (52 факториал), то есть, 80658175170943878571660636856403766975289505440883277824000000000000 или примерно 8,0658 × 1067.
Решение: Каждый возможный исход соответствует функции Разделы комбинаторики Структурная комбинаторика К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов. Экстремальная комбинаторика Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.
Теория Рамсея Основная статья: Теория Рамсея Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее: в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы. В терминах структурной комбинаторики это же утверждение формулируется так: в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3. Вероятностная комбинаторика Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества. Инфинитарная комбинаторика Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам. Правило суммы: если элемент a из некоторой совокупности элементов можно выбрать m различными способами, и независимо от этого элемент b – n способами, то выбрать a или b можно n+m способами. Правило произведения: если элемент a из некоторой совокупности элементов можно выбрать m различными способами, и независимо от этого элемент b – n способами, то выбрать a и b вместе можно n∙m способами. Задачи: 1. Сколько существует а) двузначных б) трехзначных в) n-значных натуральных чисел? Решение: а) 9∙10=90 б) 9∙10∙10=900 в) 9∙10∙10∙…∙10=9∙10n-1 2. Каково максимальное количество абонентов могут обслуживаться одной сотовой сетью, если номер семизначный? Решение: Эта задача аналогична задаче на составление семизначного числа. Отличие состоит лишь в том, что число не может начинаться с нуля, а телефонный номер – может. Поэтому семизначных номеров 107=10000000. Ответ: десять миллионов абонентов могут обслуживаться в одной сотовой сети. 3. Каково максимальное количество абонентов могут обслужить операторы всех сотовых сетей? Решение: Номер сети состоит из трех знаков, причем первая цифра во всех сетях одинаковая: 9. Поэтому эта задача сводится к решению задачи на составление девятизначного числа, которое может начинаться с нуля. Поэтому все сотовые сети могут обслужить 109=1000000000 абонентов. Ответ: один миллиард абонентов. 4. Каких чисел - полиандромов больше, семизначных или восьмизначных? Решение: Полиандромы – это такие числа, которые читаются одинаково слева направо и справа налево. У семизначного числа – полиандрома на первой позиции может стоять любая из девяти цифр, на второй, третьей и четвертой позициях – любая из десяти. А вот на пятой, шестой и седьмой позициях цифры уже зафиксированы. Таким образом, по правилу произведения семизначных чисел – полиандромов 9∙10∙10∙10∙1∙1∙1=9000. Восьмизначных чисел – полиандромов 9∙10∙10∙10∙1∙1∙1∙1=9000. Так что семизначных и восьмизначных чисел – полиандромов поровну. Ответ: поровну. 5. Сколько существует всевозможных четырехзначных чисел, состоящих из цифр 0, 1, 2, 3, 4, 5, 7 и содержащих ровно одну тройку? Решение: Цифра «3» может занимать любую из четырех позиций. В силу того, что для записи используются всего лишь семь цифр, то на первой позиции, если там не тройка, может находиться любая из пяти цифр, так как нуль не может стоять на первой позиции, а тройка зафиксирована. На остальных позициях, где нет тройки, может находиться любая из шести цифр. Изобразим схему заполнения позиций:
3 6 6 6 5 3 6 6 5 6 3 6 5 6 6 3 В таком случае, по правилу произведения четырехзначных чисел, начинающихся с тройки, 63, а с тройкой во второй, третьей и четвертой позициях 5∙62. Таким образом, всего четырехзначных чисел, составленных из данных цифр и содержащих ровно одну тройку по правилу сложения 63+5∙62∙3=36∙(6+15)=36∙21=756. Ответ: 756. 6. Сколько существует четырехзначных чисел, кратных пяти и состоящих из цифр 0, 2, 5, 7, 9, если каждое число состоит из различных цифр? Решение: Числа, кратные пяти, оканчиваются на «0» или «5». На первой позиции может находиться любая из предложенных пяти цифр, кроме нуля и зафиксированной последней цифры. Изобразим схему заполнения позиций: 4 3 2 0 3 3 2 5 Таким образом, чисел, составленных из предложенных цифр и оканчивающихся на «0» по правилу произведения 4∙3∙2=24, а оканчивающихся на «5» 3∙3∙2=18. Всего чисел, кратных пяти, по правилу сложения 24+18=42. Ответ: 42. 7. Сколько существует шестизначных чисел, в записи которых присутствует хотя бы одна четная цифра? Решение: По правилу произведения всего шестизначных чисел 9∙105=900000. Для составления чисел, в которых нет ни одной четной цифры, используются пять цифр, поэтому таких чисел 56=15625. Таким образом, чтобы найти количество шестизначных чисел, в которых присутствует хотя бы одна четная цифра, нужно из числа всех возможных вариантов вычесть число неблагоприятных: 900000-15625=884375. Ответ: 884375. Вероятность событий При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Например, при последовательном извлечении из колоды пяти карт более возможна ситуация, когда появились карты разных мастей, чем появление пяти карт одной масти; при десяти бросках монеты более возможно чередование гербов и цифр, нежели выпадение подряд десяти гербов, и т.д. Поэтому с каждым таким событием связывают по определенному правилу некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события и является вторым основным понятием теории вероятностей. Отметим, что само понятие вероятности, как и понятие случайного события, является аксиоматическим и поэтому не поддается строгому определению. То, что в дальнейшем будет называться различными определениями вероятности, представляет собой способы вычисления этой величины.
Если все события, которые могут произойти в результате данного опыта, а) попарно несовместны; б) равновозможны; в) образуют полную группу, то говорят, что имеет место схема случаев. Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их число равно п (число возможных исходов), а при т из них происходит некоторое событие А (число благоприятных исходов). Вероятностью события А называется отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов: - классическое определение вероятности. Свойства вероятности. Из определения 1.8 вытекают следующие свойства вероятности: 1. Вероятность достоверного события равна единице. Доказательство. Так как достоверное событие всегда происходит в результате опыта, то все исходы этого опыта являются для него благоприятными, то есть т = п, следовательно, Р(А) = 1. 2. Вероятность невозможного события равна нулю. Доказательство. Для невозможного события ни один исход опыта не является благопри-ятным, поэтому т = 0 и р(А) = 0. 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Доказательство. Случайное событие происходит при некоторых исходах опыта, но не при всех, следовательно, 0 < m < n, и из (1.1) следует, что 0 < p(A) < 1. Геометрическая вероятность Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности. Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошен-ная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле: (2.1) где l — длина отрезка l, а L — длина отрезка L. Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s: (2.1`) где s — площадь части области, а S — площадь всей области. В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой: (2.1``) где v — объем части тела, а V — объем всего тела. 3.Теоремы теории вероятностей. Теорема сложения вероятностей несовместимых событий. Полная группа событий. Противоположные события. Теорема1. (теорема сложения). Вероятность р (А + В) суммы событий А и В равна Р (А + В) = р (А) + р (В) — р (АВ). (2.2) Доказательство. Докажем теорему сложения для схемы случаев. Пусть п — число возможных исходов опыта, тА — число исходов, благоприятных событию А, тВ — число исходов, благопри-ятных событию В, а тАВ — число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно тА + тВ — тАВ (так как в сумме (тА + тВ) тАВ учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1):
что и требовалось доказать. Теорему1 можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С Р (А + В + С) = р (А) + р (В) + р (С) — р (АВ) — р (АС) — р (ВС) + р (АВС) Теорема 2. Сумма вероятностей противоположных событий равна 1: р (А) + р () = 1. Доказательство. Так как А и образуют полную группу, то одно из них обязательно произойдет в результате опыта, то есть событие А + является достоверным. Следовательно, Р (А +) = 1. Но, так как А и несовместны, из (2.4) следует, что Р (А +) = р (А) + р (). Значит, р (А) + р () = 1, что и требовалось доказать. Замечание. В ряде задач проще искать не вероятность заданного события, а вероятность события, противоположного ему, а затем найти требуемую вероятность по формуле (2.5). Формулировка Пусть дано вероятностное пространство
Замечание Формула полной вероятности также имеет следующую интерпретацию. Пусть
Тогда
т.е. априорная вероятность события равна среднему его апостериорной вероятности. 10 Теорема Байеса (или формула Байеса) — одна из основных теорем теории вероятностей, которая позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны. Названа в честь её автора, преп. Томаса Байеса (посвящённая ей работа «An Essay towards solving a Problem in the Doctrine of Chances» впервые опубликована в 1763 году,[1] через 2 года после смерти автора). Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений. Психологические эксперименты[2] показали, что люди при оценках вероятности игнорируют различие априорных вероятностей (ошибка обоснования оценки (англ.)русск.), и потому результаты по формуле Байеса и правильные результаты могут сильно отличаться от ожидаемых. Формулировка
Вывод формулы [показать] «Физический смысл» и терминология Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они — предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии). Следствие Формула Байеса является важным следствием из формулы полной вероятности события, зависящего от нескольких несовместных гипотез (и только от них!).
Вывод формулы [показать] Пример Событие B — в баке нет бензина, событие A — машина не заводится. Заметим, что вероятность Р(А|В) того, что машина не заведется, если в баке нет бензина, равняется единице. Тем самым, вероятность Р(В) того, что в баке нет бензина, равна произведению вероятности Р(А) того, что машина не заводится, на вероятность P(B|A) того, что причиной события А стало именно отсутствие бензина (событие В), а не, к примеру, разряженный аккумулятор. Пример расчёта Пусть вероятность брака у первого рабочего Cобытие
По формуле Байеса получим:
11 Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу. Формулировка Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность Доказательство Так как в результате Обозначим
При этом вероятность каждой комбинации равна произведению вероятностей:
Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:
Пример. Игральная кость бросается 4 раза. При каждом броске нас интересует событие А={выпала шестерка}. Решение: Здесь четыре испытания, и т.к. кубик симметричен, то p=P(A)=1/6, q=1-p=5/6. Вероятность того, что в 4 независимых испытаниях успех наступит ровно m раз (m < 4), выражается формулой Бернулли:
Посчитаем эти значения и запишем их в таблицу.
Самое вероятное число успехов в нашем случае m0=0. Пример. Вероятность появления успеха равна 3/5. Найти наивероятнейшее число наступлений успеха, если число испытаний равно 19, 20. Решение: при n =19 находим
На практике в случае, когда n велико, а p мало (обычно p < 0,1; npq < 10) вместо формулы Бернулли применяют приближенную формулу Пуассона
Пуассоновское приближение Верна предельная теорема Пуассона: Пусть
Другими словами, в описанном предельном переходе биномиальные вероятности Доказательство. Для краткости будем считать, что
поскольку выражение в квадратных скобках стремится к единице, если
Замечание 2.10 Формулировка теоремы Пуассона, которая приведена выше, ничего не говорит о скорости сходимости биномиального распределения к предельному пуассоновскому закону. Ответ на этот вопрос можно дать, воспользовавшись, например, теоремой из [14, гл. 3, § 12]. Из нее вытекает, что если
где Нормальное приближение Здесь мы рассмотрим случай, когда число испытаний в схеме Бернулли растет ( Интегральная теорема Муавра-Лапласа 1 Пусть
где Мы не приводим доказательства этого утверждения, желающие могут найти его, например, в [4] или [14]. Мы ограничимся рядом замечаний. Замечание 2.11 Функция Замечание 2.12 Чтобы понять смысл выражения
необходимо вспомнить, что Замечание 2.13 В предельном переходе ``
таким образом, в последней сумме содержится много (порядка Замечание 2.14 Скорость сходимости в (12) хорошо изучена. Имеет место так называемая оценка Берри-Эссеена: существует такое
Подробности можно найти в [14]. Применение Используется в теории вероятностей. При рассмотрении количества
требует громоздких вычислений, так как нужно суммировать большое число определённых по этой формуле вероятностей. Поэтому используют асимптотическое выражение для биномиального распределения при условии, что Формулировка Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина
где Приближённую формулу
рекомендуется применять при n > 100 и npq > 20. Доказательство Для доказательства Теоремы будем использовать формулу Стирлинга из математического анализа:
где
даёт малую относительную ошибку, быстро стремящуюся к нулю, когда Нас будут интересовать значения
Поэтому использование приближённой формулы Стирлинга для замены факториалов в биномиальном распределении допустимо, и мы получаем
Также понадобится использование отклонения относительной частоты от наивероятнейшего значения
Переписываем полученное ранее биномиальное распределение с факториалами, заменёнными по приближённой формуле Стирлинга:
Предположим, что
Взяв логарифм второго и третьего множителей равенства (6), применим разложение в ряд Тейлора:
Располагаем члены этого разложения по степеням
Предположим, что при
Это условие, как уже было указанно выше, означает, что рассматриваются значения Теперь, пренебрегая вторым и последующими членами в разложении (6), получаем, что логарифм произведения второго и третьего членов произведения в правой части (8) равен
Отбрасывая малые слагаемые в скобках первого множителя (6), получаем:
Обозначив
Переписываем (12) в виде:
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.47.14 (0.158 с.) |
 . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом
. Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом  .
. , которая в свою очередь задаётся аксиоматически и вместе с пространством элементарных событий
, которая в свою очередь задаётся аксиоматически и вместе с пространством элементарных событий  образует вероятностное пространство
образует вероятностное пространство  .
. . Будем выбирать из этого множества различные упорядоченные подмножества
. Будем выбирать из этого множества различные упорядоченные подмножества  из k элементов.
из k элементов.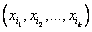 элементов множества Х.
элементов множества Х. из m -элементного множества в n -элементное, удовлетворяющих заданным ограничениям?
из m -элементного множества в n -элементное, удовлетворяющих заданным ограничениям? (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.
(аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати. , и полная группа попарно несовместных событий
, и полная группа попарно несовместных событий  , таких что
, таких что 


 . Пусть
. Пусть  — интересующее нас событие. Тогда
— интересующее нас событие. Тогда .
. — случайная величина, имеющая распределение
— случайная величина, имеющая распределение .
. ,
, ,
где
,
где
 — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);
— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);
 — вероятность гипотезы A при наступлении события B (апостериорная вероятность);
— вероятность гипотезы A при наступлении события B (апостериорная вероятность);
 — вероятность наступления события B при истинности гипотезы A;
— вероятность наступления события B при истинности гипотезы A;
 — полная вероятность наступления события B.
— полная вероятность наступления события B.
 — вероятность наступления события B, зависящего от ряда гипотез
— вероятность наступления события B, зависящего от ряда гипотез  , если известны степени достоверности этих гипотез (например, измерены экспериментально);
, если известны степени достоверности этих гипотез (например, измерены экспериментально); , у второго рабочего —
, у второго рабочего —  , а у третьего —
, а у третьего —  . Первый изготовил
. Первый изготовил  деталей, второй —
деталей, второй —  деталей, а третий —
деталей, а третий —  деталей. Начальник цеха берёт случайную деталь, и она оказывается бракованной. Спрашивается, с какой вероятностью эту деталь изготовил третий рабочий?
деталей. Начальник цеха берёт случайную деталь, и она оказывается бракованной. Спрашивается, с какой вероятностью эту деталь изготовил третий рабочий? — брак детали, событие
— брак детали, событие  . Тогда
. Тогда  , где
, где  , а
, а  . По формуле полной вероятности
. По формуле полной вероятности


 того, что событие A наступит k раз в n независимых испытаниях, равна:
того, что событие A наступит k раз в n независимых испытаниях, равна:  , где
, где  .
. независимых испытаний, проведенных в одинаковых условиях, событие
независимых испытаний, проведенных в одинаковых условиях, событие  наступает с вероятностью
наступает с вероятностью  , следовательно, противоположное ему событие с вероятностью
, следовательно, противоположное ему событие с вероятностью  .
. раз, тогда остальные
раз, тогда остальные  раз это событие не наступает. Событие
раз это событие не наступает. Событие  .
. .
.



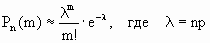
 ,
,  таким образом, что
таким образом, что  , где
, где  -- заданное число. Тогда для любого фиксированного
-- заданное число. Тогда для любого фиксированного 

 аппроксимируются пуассоновским распределением.
аппроксимируются пуассоновским распределением. . Тогда
. Тогда








 , то
, то
 -- пуассоновская с.в. с параметром
-- пуассоновская с.в. с параметром  остается фиксированной. Верна так называемая интегральная теорема Муавра-Лапласа.
остается фиксированной. Верна так называемая интегральная теорема Муавра-Лапласа. -- число успехов в последовательности из
-- число успехов в последовательности из  независимых испытаний Бернулли с вероятностью успеха в единичном испытании
независимых испытаний Бернулли с вероятностью успеха в единичном испытании  . При
. При 
 .
. , появившаяся в этой теореме, называется функцией распределения стандартного нормального закона. Для значений этой функции существуют подробные таблицы. Свойства функции
, появившаяся в этой теореме, называется функцией распределения стандартного нормального закона. Для значений этой функции существуют подробные таблицы. Свойства функции  5.2.
5.2.
 и
и  (см. Пример 2.7). Таким образом, это выражение имеет вид
(см. Пример 2.7). Таким образом, это выражение имеет вид  . Легко видеть, что
. Легко видеть, что  , а
, а  . Преобразование (13) называется центрированием и нормированием случайной величины
. Преобразование (13) называется центрированием и нормированием случайной величины 
 ) слагаемых.
) слагаемых. , что
, что
 появлений события
появлений события  и
и  . Так как при достаточно больших
. Так как при достаточно больших 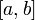 содержит большое число единиц, то непосредственное использование биномиального распределения
содержит большое число единиц, то непосредственное использование биномиального распределения
 фиксированно, а
фиксированно, а  . Теорема Муавра-Лапласа утверждает, что таким асимптотическим выражением для биномиального распределения является нормальная функция.
. Теорема Муавра-Лапласа утверждает, что таким асимптотическим выражением для биномиального распределения является нормальная функция. ограничена равномерно по m и n
ограничена равномерно по m и n  , то
, то
 , c > 0, c — постоянная.
, c > 0, c — постоянная.
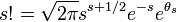 (1)
(1) . При больших
. При больших  величина
величина  очень мала, и приближённая формула Стирлинга, записанная в простом виде,
очень мала, и приближённая формула Стирлинга, записанная в простом виде, (2)
(2) .
. ,
,  (3)
(3) (4)
(4)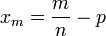 (5)
(5) (6)
(6) (7)
(7)
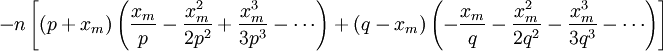 (8)
(8)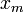 :
: (9)
(9) (10)
(10) (11)
(11) (12)
(12) (13)
(13) (14)
(14)


