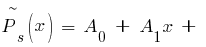Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения, решающиеся непосредственным интегрированием
Рассмотрим уравнение n-го порядка:
Оно решается непосредственным интегрированием.
........
Пример. Решить уравнение:
Решение. Преобразуем, применяя формулу тригонометрии:
Интегрируем:
Интегрируем еще раз:
Решение линейных однородных ДУ с постоянными коэффициентами Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами:
Его решение можно получить следуя общему методу понижения порядка. Однако проще сразу получить фундаментальную систему n линейно независимых решений и на ее основе составить общее решение. При этом вся процедура решения сводится к следующим шагам. Ищем решение уравнения (1) в виде ekx. Получаем характеристическое уравнение:
Оно имеет n корней. Решаем уравнение (2) и находим его корни ki. Тогда характеристическое уравнение можно представить в виде:
Каждому корню соответствует одно из линейно независимых решений yi фундаментальной системы решений уравнения (1). Тогда общее решение уравнения (1) имеет вид:
Установление вида частного решения Составим характеристическое уравнения однородного уравнения (3):
Пусть ki - корни характеристического уравнения (4). Комплексные корни выразим через действительную и мнимую части:
Для действительных корней k2i = 0. Если среди корней ki нет значения
то частное решение имеет вид:
где s - наибольшее из s1 и s2;
многочлены степени s с коэффициентами Ai, Bi, которые подлежат определению подстановкой в уравнение (2). Если среди корней ki есть корень
кратности m, то частное решение имеет вид:
После того как установлен вид частного решения, подставляем y1 в уравнение (2) и находим неизвестные коэффициенты Ai и Bi. После чего получаем общее решение уравнения (2):
Далее рассмотрен пример решения неоднородного дифференциального уравнения со специальной неоднородной частью. Частные случаи Неоднородность в виде многочлена
В этом случае α = β = 0. Если среди корней ki нет значения
то частное решение имеет вид:
Если среди корней ki есть корень
кратности m, то частное решение имеет вид:
Неоднородность в виде экспоненты
В этом случае β = 0. Если среди корней ki нет действительного значения
то частное решение имеет вид:
Если среди корней ki есть корень
кратности m, то частное решение имеет вид:
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 171; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.150.59 (0.009 с.) |
















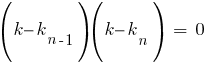


 Решение линейных неоднородных ДУ с постоянными коэффициентами
Решение линейных неоднородных ДУ с постоянными коэффициентами