
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение дифференциальных уравненийСтр 1 из 3Следующая ⇒ Дифференциальные уравнения Определение дифференциальных уравнений Дифференциальные уравнения – это соотношение вида F(x1,x2,x3,..,y,y′,y′′,...y(n)) = 0, связывающее независимые переменные x1,x2,x3,... функцию y этих независимых переменных и ее производные до n-го порядка. При этом функция F определена и достаточное число раз дифференцируема в некоторой области изменения своих аргументов. Обыкновенные дифференциальные уравнения – это дифференциальные уравнения, в которых содержится только одна независимая переменная. Дифференциальные уравнения в частных производных – это дифференциальные уравнения, в которых содержится две и более независимых переменных. Как обыкновенные дифференциальные уравнения, так и уравнения в частных производных можно разделить на линейные и нелинейные. Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Теория линейных ДУ развита значительно глубже, чем теория нелинейных уравнений. Нелинейные дифференциальные уравнения в общем случае не имеют разработанных методов решения, кроме некоторых частных классов. В некоторых случаях (с применением тех или иных приближений) они могут быть сведены к линейным. y'' - sin x y' + ( cos x) y = tg x - линейное, sin y' - cos y = ctg x - нелинейное, y''' - y' = 0- линейное, (y IV ) 2 - 3 y''' + y = 1 - нелинейное.
Классификация дифференциальных уравнений Порядок дифференциального уравнения – это порядок старшей входящей в него производной. Степень дифференциального уравнения – это показатель степени, в которую возведена производная наивысшего порядка. Вот пример уравнения первого порядка второй степени: Дифференциальные уравнения первого порядка Дифференциальные уравнения с разделяющимися переменными – это уравнения вида Решение дифференциальных уравнений с разделяющимися переменными В исходном уравнении:
Выразим y' через дифференциалы: Иногда уравнение задается в таком виде. Это означает, что переменные x и y равноправны.
Поскольку мы делили на s(x)r(y), то получили интеграл уравнения при s(x)≠ 0 и r(y)≠ 0. Далее следует рассмотреть решения, определяемые уравнениями s(x)= 0 и r(y)= 0, которые могут давать несколько значений типа x = const, y = const, также удовлетворяющие исходному уравнению (1). Часть этих решений может уже содержаться в решении (2). Дифференциальные уравнения высших порядков Частные случаи Дискретная математика Отрицание. Определим унарную логическую операцию — отрицание. Для этой операции таблица истинности выглядит следующим образом: Иллюстрацией отрицания в естественном языке служит частица "не", или слова "неверно, что". Например: если мы хотим отрицать, что Точка М принадлежит прямой а (1) Мы скажем Точка М не принадлежит прямой а (2) Если (1) — это высказывание, то (2) - Обратите внимание, что истинностные значения высказываний (1) и (2) находятся в определенной зависимости: если (1) — истинно, то (2) — ложно. Если (1) — ложно, то (2) — истинно. Например, покажем, что Это одно из свойств Булевой алгебры. Следует отметить, что отрицание составных формул не такая уж тривиальная операция. Чуть позднее мы проиллюстрируем это утверждение. Конъюнкция Введем еще одну логическую операцию, определив её словесно следующим образом. Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны. Эту логическую операцию называется еще логическим умножением, или логическим минимумом. Выпишем таблицу истинности для конъюнкции Свойства конъюнкции: В естественном языке эта операция чаще всего интерпретируется союзом "и" Дизъюнкция Еще одной из логических операций является операция дизъюнкции. Дизъюнкция двух элементарных высказываний истинна тогда и только тогда, когда истинно хотя бы одно из элементарных высказываний. Обозначается эта операция знаком и иногда называется логическим сложением или логическим максимумом. Таблица истинности дизъюнкции выглядит так:
4. "Исключающее или" Операция " исключающего или " задается следующей таблицей истинности, она истинна, когда истинен только один из операндов. Эту операцию еще называют строгой дизъюнкцией или логическим неравенством. Импликация Следующая логическая операция, которую мы рассмотрим — это операция импликации. Импликация ложна тогда и только тогда, когда — истинна, а — ложна. Эквивалентность Она истинна только тогда, когда значения и совпадают. Эту операцию еще иногда называют логическим равенством. В математических терминах эта операция интерпретируется в качестве фраз "тогда и только тогда", "необходимо и достаточно". Такая форма тоже очень часто используется в формулировке теорем. Эквивалентность представляется в виде: Штрих Шеффера Эта операция обозначается знаком / и определяет несовместимость высказываний. Эта операция ложна тогда и только тогда, когда оба операнда истинны. Выражение «А/В» читается так: «и В несовместны». Приведем таблицу истинности этой операции. Основные определения теории множеств. Примеры. Понятие множества является одним из фундаментальных понятий математики, которому трудно дать определение. Дело в том, что определить понятие — это значит найти такое родовое понятие, в которое это понятие входит в качестве вида, но понятие «множество» - это самое широкое понятие математики и математической логики, т.е. категория, а для категории нельзя найти более широкое, т.е. родовое понятие. Ограничимся описательным объяснением этого понятия. Множество — это набор, совокупность каких-либо вполне различаемых объектов, называемых его элементами, обладающими общими для всех их и только их свойствами, и рассматриваемых как единое целое. Поясним это понятие с помощью примеров. Можно говорить о множестве людей, живущих сейчас в России, о множестве точек данной геометрической фигуры, множестве решений данного уравнения. Обратите внимание, мы говорим о наборе вполне различимых между собой элементов, невозможно говорить о множестве капель в стакане воды, так как невозможно четко и ясно указать каждую отдельную каплю. Какова же структура множества, чем одно множество отличается от другого, какие математические и логические операции определены для множества? Прежде всего, каждое множество состоит из того или иного набора объектов, которые называются элементами множества. Факт, что элемент а принадлежит множеству Х мы будем обозначать: а Î Х.
Порядок элементов в множестве несущественен. Множества { а, в, с } и { а, с, в } одинаковы. Множество может задаваться: 1. путем перечисления его элементов. Обычно перечислением задают конечные множества. 2. путем описания свойств, общих для всех элементов этого множества, и только этого множества. Это свойство называется характеристическим свойством, а такой способ задания множества описанием. Таким образом, можно задавать как конечные, так и бесконечные множества. Если мы задаем множество каким-либо свойством, потом может оказаться, что этим свойством обладает всего лишь один объект или вообще такого объекта нет. Данный факт может быть совсем не очевиден. Например: множество натуральных чисел, больших 1, таких что, уравнение
Если характеристическим свойством, задающим множество. А не обладает ни один объект, то говорят, что множество А пустое. Обозначается это так: Æ. Понятие пустого множества очень важное понятие. Оно позволяет описательно задавать множества, не заботясь, есть ли в этом множестве элементы и совершенно спокойно оперировать с этими множествами. Пустое множество будем считать конечным множеством. Например: множество действительных корней уравнения
Множества бывают конечными или бесконечными. Если число элементов множества конечно — множество называется конечным. Определение: Количество элементов, составляющих множество, называется мощностью множества. Определение: Если между элементами бесконечного множества можно установить взаимооднозначное соответствие с элементами множества положительных целых чисел, то говорят, что множество счетно. Например: множество действительных чисел, множество частных решений дифференциального уравнения - бесконечные множества. множество чисел, делящихся без остатка на 3 — счетное множество, множество букв русского алфавита, множество отличников вашей группы — конечно. Определение: Два множества равны между собой, если они состоят из одних и тех же элементов. Т.е. любой элемент множества Х является элементом множества Y, и любой элемент множества Y является элементом множества Х. Тема 2.2 Подмножество. Понятие универсального множества. Подмножество Определение: Множество Х является подмножеством Y, если любой элемент множества Х принадлежит множеству Y. Это еще называется нестрогим включением. Некоторые свойства подмножества: 1. ХÍХ - рефлективность 2. X Í Y & YÍZ ® X Í Z - транзитивность 3. Æ Í X т.е. пустое множество является подмножеством любого множества. Универсальное множество Определение: Универсальное множество — это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области, т.е. 1. Если М Î I, то М Í I 2. Если М Î I, то Ώ(М) Í I, где под Ώ(М) — понимаются все возможные подмножества М, или Булеан М. Универсальное множество обычно обозначается I. Универсальное множество может выбираться самостоятельно, в зависимости от рассматриваемого множества, и решаемых задач. Рассматривая множество целых положительных чисел, в качестве универсального множества можно взять и множество целых чисел, и множество действительных чисел, и множество комплексных чисел, и само множество целых положительных чисел. Более подробно о свойствах универсального множества мы поговорим, обсуждая операции над множествами. Скажем только, что если роль нуля в алгебре множеств играет пустое множество. То универсальное множество, играет роль единицы в алгебре множеств. Тема 2.3 Операции над множествами. Теперь определим операции над множествами. Пересечение множеств. Определение: Пересечением множеств Х и У называется множество, состоящее из всех тех, и только тех элементов, которые принадлежат и множеству Х и множеству У. Например: Х={1,2,3,4} У={2,4,6} пересечением {2,4} Определение: Множества называются непересекающимися, если не имеют общих элементов, т.е. их пересечение равно пустому множеству. Например: непересекающимися множествами являются множества отличников группы и неуспевающих. Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих одновременно всем множествам. Свойства пересечения: 1. X∩Y = Y∩X - коммутативности 2. (X∩Y) ∩Z =X∩ (Y∩Z)=X∩Y∩Z - ассоциативности 3. X∩Æ = Æ 4. X∩ I = Х Объединение множеств Определение: Объединением двух множеств называется множество, состоящее из всех и только тех элементов, которые принадлежат хотя бы одному из множеств Х или У. Например: Х={1,2,3,4} У={2,4,6} объединением {1,2,3,4,6} Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих хотя бы одному из этих множеств. Свойства объединения: 1. XUY= YUY- коммутативности 2. (X UY)UZ =XU (YUZ)=XUYUZ - ассоциативности 3. XUÆ = X 4. XU I = I Из свойств операций пересечения и объединения видно, что пустое множество аналогично нулю в алгебре чисел. Разность множеств Определение: Данная операция, в отличие от операций пересечения и объединения определена только для двух множеств. Разностью множеств Х и У называется множество, состоящее их всех тех и только тех элементов, которые принадлежат Х и не принадлежат У. Например: Х={1,2,3,4} У={2,4,6} разность {1,3} Как мы уже видели, роль нуля в алгебре множеств играет пустое множество. Определим множество, которое будет играть роль единицы в алгебре множеств Дополнение множества Дополнением множества Х называется разность I и Х. Свойства дополнения:
Дифференциальные уравнения Определение дифференциальных уравнений Дифференциальные уравнения – это соотношение вида F(x1,x2,x3,..,y,y′,y′′,...y(n)) = 0, связывающее независимые переменные x1,x2,x3,... функцию y этих независимых переменных и ее производные до n-го порядка. При этом функция F определена и достаточное число раз дифференцируема в некоторой области изменения своих аргументов. Обыкновенные дифференциальные уравнения – это дифференциальные уравнения, в которых содержится только одна независимая переменная. Дифференциальные уравнения в частных производных – это дифференциальные уравнения, в которых содержится две и более независимых переменных. Как обыкновенные дифференциальные уравнения, так и уравнения в частных производных можно разделить на линейные и нелинейные. Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Теория линейных ДУ развита значительно глубже, чем теория нелинейных уравнений. Нелинейные дифференциальные уравнения в общем случае не имеют разработанных методов решения, кроме некоторых частных классов. В некоторых случаях (с применением тех или иных приближений) они могут быть сведены к линейным. y'' - sin x y' + ( cos x) y = tg x - линейное, sin y' - cos y = ctg x - нелинейное, y''' - y' = 0- линейное, (y IV ) 2 - 3 y''' + y = 1 - нелинейное.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.206.169 (0.004 с.) |




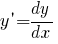 ;
;  ;
;  ;
;




