
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения
Метод состоит в замене произвольных постоянных
соответствующего однородного уравнения
на вспомогательные функции
Определителем системы (1) служит вронскиан функций Если
является решением исходного линейного неоднородного дифференциального уравнения. 16. Интегрирование ЛНДУ
Дифференциальное уравнение называется линейным, если неизвестная функция и все ее производные входят в уравнение линейно:
Если f (x) тождественно равна нулю, то уравнение называется однородным; в противном случае оно называется неоднородным.
Метод подбора частного решения неоднородного уравнения с правой частью специального вида. Методом Лагранжа может быть решено любое неоднородное уравнение с постоянными коэффициентами. Однако если свободный член в уравнении (20) имеет вид
где Pm 1(x) и Qm 2(x) - многочлены степеней, соответственно, m 1 и m 2, можно сразу указать вид частного решения в форме с неопределёнными коэффициентами. Общее правило таково: составим из коэффициентов при x в экспоненте и тригонометрических функциях число
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.12.172 (0.006 с.) |

 в общем решении
в общем решении

 , производные которых удовлетворяют линейной алгебраической системе
, производные которых удовлетворяют линейной алгебраической системе
 , что обеспечивает её однозначную разрешимость относительно
, что обеспечивает её однозначную разрешимость относительно  .
. — первообразные для
— первообразные для 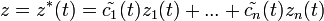
 -го (второго) порядка с постоянными коэффициентами и правой частью специального вида.
-го (второго) порядка с постоянными коэффициентами и правой частью специального вида.

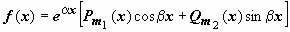 .
.
 и пусть r - кратность числа s 0 как корня характеристического уравнения, m = max(m 1, m 2). Тогда частное решение надо искать в виде
и пусть r - кратность числа s 0 как корня характеристического уравнения, m = max(m 1, m 2). Тогда частное решение надо искать в виде  , где Rm (x) и Sm (x) - многочлены степени m с неопределёнными коэффициентами. Дифференцируя функцию y чн n раз, подставив эти производные в уравнение и приравнивая коэффициенты при одинаковых степенях x и одинаковых тригонометрических функциях (sin x или cos x), получим систему из 2(m + 1) уравнений относительно 2(m + 1) неопределённых коэффициентов многочленов Rm (x) и Sm (x). Решив эту систему, определим коэффициенты функции y чн(x).
, где Rm (x) и Sm (x) - многочлены степени m с неопределёнными коэффициентами. Дифференцируя функцию y чн n раз, подставив эти производные в уравнение и приравнивая коэффициенты при одинаковых степенях x и одинаковых тригонометрических функциях (sin x или cos x), получим систему из 2(m + 1) уравнений относительно 2(m + 1) неопределённых коэффициентов многочленов Rm (x) и Sm (x). Решив эту систему, определим коэффициенты функции y чн(x). 


