
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение Клеро
Рассмотрим дифференциальное уравнение следующего вида
Такое уравнение носит название уравнения Клеро. Легко видеть, что уравнение Клеро — частный случай уравнения Лагранжа, когда Положим
Продифференцируем это уравнение по
Преобразуем его в вид
Приравнивая каждый множитель к нулю, получим
и
Интегрируя уравнение
С геометрической точки зрения, этот интеграл представляет собой семейство прямых линий. Если из уравнения
Которая, как легко показать, является решением уравнения
Но поскольку
Решение
или, что без разницы, исключением
Следовательно, особое решение уравнения Клеро, определяет огибающую семейства прямых, заданных общим интегралом 11. Понятие обыкновенного дифференциального уравнения
Уравнение вида
называется обыкновенным дифференциальным уравнением n-го порядка. Решением этого уравнения является произвольная функция y = y (x), подстановка которой в уравнение превращает его в верное тождество. График решения дифференциального уравнения называется интегральной кривой.. Частным решением уравнения (1) на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция, удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество. Общее решение дифференциального уравнения — функция наиболее общего вида, которая при подстановке в дифференциальное уравнение вида
обращает его в тождество. Если каждое решение дифференциального уравнения представимо в виде:
где
при всех допустимых значениях параметров (неопределённых констант) Рассмотрим более подробно вопрос, о геометрическом истолковании уравнения второго порядка Уравнение второго порядка имеет общий вид F (x, y, y ', y '') = 0. (8.1) Его всегда можно переписать так:
Так как 12. Уравнения, допускающие понижение порядка. Дифференциальное уравнение n -го порядка имеет вид F (x, y, y ', …, y (n)) = 0. (9.1) Если уравнение (9.1) F (x, y, y ', …, y (n)) = 0 разрешимо относительно старшей производной y (n), то оно примет вид y (n) = f (x, y, y ', …, y (n – 1)). (9.2) Рассмотрим некоторые типы уравнений, допускающие понижение порядка.
Уравнение вида y (n) = f (x). Решение дифференциального уравнения сводится к последовательному применению квадратур. Общее решение содержит n произвольных постоянных. Уравнение вида F (x, y ', …, y (n)) = 0, Сделав замену y ' = z, где z = z (x), сводим данное уравнение к уравнению более низкого порядка. Решив его, заменяем z = y ' и находим y. Уравнение вида F (x, y (k), y (k + 1), …, y (n)) = 0, Производим замену y (k) = z, где z = z (x). Решив полученное уравнение, заменяем z = y (k) и интегрированием находим y. Уравнение вида F (y, y ', …, y (n)) = 0, Сделав замену y ' = z, где z = z (y), получим дифференциальное уравнение (n – 1)-го порядка, связывающее y, z и производные от z по y.
13. Линейные однородные дифференциальные уравнения
Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение В случае, если Теорема 1 о линейности пространства частных решений линейного однородного дифференциального уравнения. Множество частных решений линейного однородного дифференциального уравнения образует линейное пространство.
Фундаментальной системой решений линейного однородного дифференциального уравнения n -го порядка называется любая линейно независимая система y 1(x), y 2(x), …, yn (x) его n частных решений Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y (x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: 14. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Интегрирование ЛОДУ
Уравнение вида
где a 1, …, an – некоторые постоянные, называется линейным дифференциальным уравнением с постоянными коэффициентами В общем случае у однородного линейного дифференциального уравнения с постоянными коэффициентами
15. Линейные неоднородные дифференциальные уравнения
Дифференциальное уравнение называется линейным, если неизвестная функция и все ее производные входят в уравнение линейно:
Если f (x) тождественно равна нулю, то уравнение называется однородным; в противном случае оно называется неоднородным. Терема 1 о структуре общего решения линейного неоднородного дифференциального уравнения. Общее решение линейного неоднородного дифференциального уравнения с непрерывными на интервале (a, b) коэффициентами и правой частью
равно сумме общего решения соответствующего однородного уравнения
и частного решения неоднородного уравнения (20) Теорема 2 о наложении решений. Если y 1,чн(x) - частное решение неоднородного уравнения Ln (y) = f 1(x), y 2,чн(x) - частное решение неоднородного уравнения Ln (y) = f 2(x), то функция
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.47.253 (0.023 с.) |



 . Интегрируется оно так же путём введения вспомогательного параметра. Найдём его решение.
. Интегрируется оно так же путём введения вспомогательного параметра. Найдём его решение. . Тогда пишем:
. Тогда пишем:

 , так же, как это делали с уравнением Лагранжа, замечая, что
, так же, как это делали с уравнением Лагранжа, замечая, что  , пишем
, пишем





 . Подставим значение
. Подставим значение 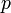 в уравнение
в уравнение 




 . Поэтому подставляя функцию
. Поэтому подставляя функцию  .
. . Это решение — суть особое решение, которое получается вследствие исключения параметра
. Это решение — суть особое решение, которое получается вследствие исключения параметра 

 -го порядка. Понятие частного и общего решения ОДУ
-го порядка. Понятие частного и общего решения ОДУ 


 — конкретные числа, то функция вида
— конкретные числа, то функция вида
 называется общим решением дифференциального уравнения.
называется общим решением дифференциального уравнения. = 0. (8.2)
= 0. (8.2) кривизна кривой y = y (x) в точке (x, y), то из формулы (8.2)
кривизна кривой y = y (x) в точке (x, y), то из формулы (8.2)  =
= 
 =
=  функций. Теорема об определителе Вронского для линейно независимых решений ЛОДУ
функций. Теорема об определителе Вронского для линейно независимых решений ЛОДУ  — однородно, если
— однородно, если  .
. , говорят о неоднородном дифференциальном уравнении
, говорят о неоднородном дифференциальном уравнении Следствие. Если y 1(x), y 2(x), …, yn (x) - частные решения уравнения (25), то их линейная комбинация C 1 y 1(x) + C 2 y 2(x) + …+ Cnyn (x) - тоже частное решение этого уравнения.
Следствие. Если y 1(x), y 2(x), …, yn (x) - частные решения уравнения (25), то их линейная комбинация C 1 y 1(x) + C 2 y 2(x) + …+ Cnyn (x) - тоже частное решение этого уравнения. , то система функций y 1(x), y 2(x), …, yn (x) линейно зависима, и её определитель Вронского тождественно равен нулю на (a, b).
, то система функций y 1(x), y 2(x), …, yn (x) линейно зависима, и её определитель Вронского тождественно равен нулю на (a, b).  на интервале (a, b) (что означает линейную зависимость этих решений на (a, b)), либо
на интервале (a, b) (что означает линейную зависимость этих решений на (a, b)), либо  в любой точке этого интервала (что означает линейную независимость этих решений на (a, b)).
в любой точке этого интервала (что означает линейную независимость этих решений на (a, b)).
 имеется так называемое характеристическое уравнение
имеется так называемое характеристическое уравнение  Корни этого уравнения – характеристические числа – являются показателями степеней слагаемых, входящих в решение. Если среди корней уравнения
Корни этого уравнения – характеристические числа – являются показателями степеней слагаемых, входящих в решение. Если среди корней уравнения  нет кратных, то решением однородного уравнения является функция вида
нет кратных, то решением однородного уравнения является функция вида  где все
где все  – некоторые константы, зависящие от начальных условий. Количество слагаемых в этой функции совпадает со степенью дифференциального уравнения. Если же, скажем,
– некоторые константы, зависящие от начальных условий. Количество слагаемых в этой функции совпадает со степенью дифференциального уравнения. Если же, скажем,  – корень характеристического уравнения кратности m, то соответствующее слагаемое принимает вид
– корень характеристического уравнения кратности m, то соответствующее слагаемое принимает вид  а общее количество слагаемых, входящих в решение однородного дифференциального уравнения уменьшается на m – 1.
а общее количество слагаемых, входящих в решение однородного дифференциального уравнения уменьшается на m – 1.
 ;
;
 ;
;
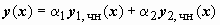 является частным решением неоднородного уравнения
является частным решением неоднородного уравнения  .
.


