
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл с параметром: группа ForСодержание книги
Поиск на нашем сайте
For1. Даны целые числа K и N (N > 0). Вывести N раз число K. For2. Даны два целых числа A и B (A < B). Вывести в порядке возрастания все целые числа, расположенные между A и B (включая сами числа A и B), а также количество N этих чисел.
For3. Даны два целых числа A и B (A < B). Вывести в порядке убывания все це- лые числа, расположенные между A и B (не включая числа A и B), а также количество N этих чисел. For4. Дано вещественное число — цена 1 кг конфет. Вывести стоимость 1, 2, …, 10 кг конфет. For5°. Дано вещественное число — цена 1 кг конфет. Вывести стоимость 0.1, 0.2, …, 1 кг конфет. For6. Дано вещественное число — цена 1 кг конфет. Вывести стоимость 1.2, 1.4, …, 2 кг конфет. For7. Даны два целых числа A и B (A < B). Найти сумму всех целых чисел от A до B включительно. For8. Даны два целых числа A и B (A < B). Найти произведение всех целых чи- сел от A до B включительно. For9. Даны два целых числа A и B (A < B). Найти сумму квадратов всех целых чисел от A до B включительно. For10. Дано целое число N (> 0). Найти сумму 1 + 1/2 + 1/3 + … + 1/ N (вещественное число). For11. Дано целое число N (> 0). Найти сумму N 2 + (N + 1)2 + (N + 2)2 + … + (2· N)2 (целое число). For12°. Дано целое число N (> 0). Найти произведение 1.1 · 1.2 · 1.3 · … (N сомножителей). For13°. Дано целое число N (> 0). Найти значение выражения 1.1 – 1.2 + 1.3 – … (N слагаемых, знаки чередуются). Условный оператор не использовать. For14. Дано целое число N (> 0). Найти квадрат данного числа, используя для его вычисления следующую формулу: N 2 = 1 + 3 + 5 + … + (2· N – 1). После добавления к сумме каждого слагаемого выводить текущее значение суммы (в результате будут выведены квадраты всех целых чисел от 1 до N). For15°. Дано вещественное число A и целое число N (> 0). Найти A в степени N: AN = A · A · … · A (числа A перемножаются N раз). For16°. Дано вещественное число A и целое число N (> 0). Используя один цикл, вывести все целые степени числа A от 1 до N.
For17. Дано вещественное число A и целое число N (> 0). Используя один цикл, найти сумму 1 + A + A 2 + A 3 + … + AN. For18. Дано вещественное число A и целое число N (> 0). Используя один цикл, найти значение выражения 1 – A + A 2 – A 3 + … + (–1) N · AN. Условный оператор не использовать. For19°. Дано целое число N (> 0). Найти произведение N! = 1·2·…· N (N–факториал). Чтобы избежать целочисленного переполнения, вычис- лять это произведение с помощью вещественной переменной и вывести его как вещественное число. For20°. Дано целое число N (> 0). Используя один цикл, найти сумму 1! + 2! + 3! + … + N! (выражение N! — N–факториал — обозначает произведение всех целых чисел от 1 до N: N! = 1·2·…· N). Чтобы избежать целочисленного пере- полнения, проводить вычисления с помощью вещественных переменных и вывести результат как вещественное число. For21. Дано целое число N (> 0). Используя один цикл, найти сумму 1 + 1/(1!) + 1/(2!) + 1/(3!) + … + 1/(N!) (выражение N! — N–факториал — обозначает произведение всех целых чисел от 1 до N: N! = 1·2·…· N). Полученное число является приближен- ным значением константы e = exp(1). For22. Дано вещественное число X и целое число N (> 0). Найти значение вы- ражения 1 + X + X 2/(2!) + … + XN /(N!) (N! = 1·2·…· N). Полученное число является приближенным значением функции exp в точке X. For23. Дано вещественное число X и целое число N (> 0). Найти значение вы- ражения X – X 3/(3!) + X 5/(5!) – … + (–1) N · X 2· N +1/((2· N +1)!) (N! = 1·2·…· N). Полученное число является приближенным значением функции sin в точке X. For24. Дано вещественное число X и целое число N (> 0). Найти значение вы- ражения 1 – X 2/(2!) + X 4/(4!) – … + (–1) N · X 2· N /((2· N)!) (N! = 1·2·…· N). Полученное число является приближенным значением функции cos в точке X. For25. Дано вещественное число X (| X | < 1) и целое число N (> 0). Найти значе- ние выражения
X – X 2/2 + X 3/3 – … + (–1) N –1· XN / N. Полученное число является приближенным значением функции ln в точке 1 + X. For26. Дано вещественное число X (| X | < 1) и целое число N (> 0). Найти значе- ние выражения X – X 3/3 + X 5/5 – … + (–1) N · X 2· N +1/(2· N +1). Полученное число является приближенным значением функции arctg в точке X. For27. Дано вещественное число X (| X | < 1) и целое число N (> 0). Найти значе- ние выражения X + 1· X 3/(2·3) + 1·3· X 5/(2·4·5) + … + + 1·3·…·(2· N –1)· X 2· N +1/(2·4·…·(2· N)·(2· N +1)). Полученное число является приближенным значением функции arcsin в точке X. For28. Дано вещественное число X (| X | < 1) и целое число N (> 0). Найти значе- ние выражения 1 + X /2 – 1· X 2/(2·4) + 1·3· X 3/(2·4·6) – … + + (–1) N –1·1·3·…·(2· N –3)· XN /(2·4·…·(2· N)).
For29. Дано целое число N (> 1) и две вещественные точки на числовой оси: A, B (A < B). Отрезок [ A, B ] разбит на N равных отрезков. Вывести H — длину каждого отрезка, а также набор точек A, A + H, A + 2· H, A + 3· H, …, B, образующий разбиение отрезка [ A, B ]. For30. Дано целое число N (> 1) и две вещественные точки на числовой оси: A, B (A < B). Отрезок [ A, B ] разбит на N равных отрезков. Вывести H — длину каждого отрезка, а также значения функции F (X) = 1 – sin(X) в точ- ках, разбивающих отрезок [ A, B ]: F (A), F (A + H), F (A + 2· H), …, F (B). For31. Дано целое число N (> 0). Последовательность вещественных чисел AK определяется следующим образом: A 0 = 2, AK = 2 + 1/ AK –1, K = 1, 2, …. Вывести элементы A 1, A 2, …, AN. For32. Дано целое число N (> 0). Последовательность вещественных чисел AK определяется следующим образом: A 0 = 1, AK = (AK –1 + 1)/ K, K = 1, 2, …. Вывести элементы A 1, A 2, …, AN. For33°. Дано целое число N (> 1). Последовательность чисел Фибоначчи FK (целого типа) определяется следующим образом:
F 1 = 1, F 2 = 1, FK = FK –2 + FK –1, K = 3, 4, …. Вывести элементы F 1, F 2, …, FN. For34. Дано целое число N (> 1). Последовательность вещественных чисел AK определяется следующим образом: A 1 = 1, A 2 = 2, AK = (AK –2 + 2· AK –1)/3, K = 3, 4, …. Вывести элементы A 1, A 2, …, AN. For35. Дано целое число N (> 2). Последовательность целых чисел AK опреде- ляется следующим образом: A 1 = 1, A 2 = 2, A 3 = 3, AK = AK –1 + AK –2 – 2· AK –3, K = 4, 5, …. Вывести элементы A 1, A 2, …, AN. Вложенные циклы For36°. Даны целые положительные числа N и K. Найти сумму 1 K + 2 K + … + NK. Чтобы избежать целочисленного переполнения, вычислять слагаемые этой суммы с помощью вещественной переменной и выводить результат как вещественное число. For37. Дано целое число N (> 0). Найти сумму 11 + 22 + … + NN. Чтобы избе- жать целочисленного переполнения, вычислять слагаемые этой суммы с помощью вещественной переменной и выводить результат как веществен- ное число. For38. Дано целое число N (> 0). Найти сумму 1 N + 2 N –1 + … + N 1. Чтобы избе- жать целочисленного переполнения, вычислять слагаемые этой суммы с помощью вещественной переменной и выводить результат как веществен- ное число. For39. Даны целые положительные числа A и B (A < B). Вывести все целые числа от A до B включительно; при этом каждое число должно выводиться столько раз, каково его значение (например, число 3 выводится 3 раза). For40. Даны целые числа A и B (A < B). Вывести все целые числа от A до B включительно; при этом число A должно выводиться 1 раз, число A + 1 должно выводиться 2 раза и т. д.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.135.226 (0.008 с.) |

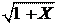 Полученное число является приближенным значением функции.
Полученное число является приближенным значением функции.


