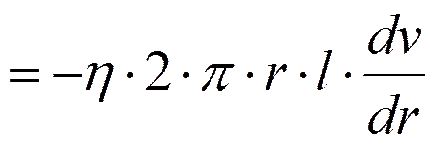Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энтропия, ее статистическое толкование и связь с термодинамической вероятностью.Стр 1 из 3Следующая ⇒
Энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов). Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии
Так как.
при изотермическом процессе (T1=T2) Согласно Больцману энтропия S системы и термодинамическая вероятность связаны между собой следующим образом: S = k lnW где k — постоянная Больцмана. Цикл Карно и его к. п. д. для идеального газа
Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T 1) и холодильников (Т 2 ), наибольшим к. п. д. обладают обратимые машины;
Работа, совершаемая в результате кругового процесса,
Откуда
13. Явления переноса. Законы диффузии, теплопроводности и внутреннего трения (вязкости) и их обоснование в молекулярно-кинетической теории. Движение жидкости (газа) по трубам. Формула Пуазейля.
Выведем основное уравнение явления переноса:
j - переносимый параметр Dx = 2<l>
<l> – средняя длина свободного пробега молекул.
1) Диффузия j = m;
2) Теплопроводность
3.Внутреннее трение
j = p = mV
Рейнольдс установил, что характер течения зависит от безразмерной величины, называемой числом Рейнольдса: r — плотность жидкости; (v)—средняя по сечению трубы скорость жидкости; d — характерный линейный размер, например диаметр трубы. При малых значениях числа Рейнольдса (Re£1000) наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области 1000£:Re£2000, а при Re = 2300 (для гладких труб) течение — турбулентное. Если число Рейнольдса одинаково, то режим течения различных жидкостей (газов) в трубах разных сечений одинаков. Методы определения вязкости 1. Метод Стокса. Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.
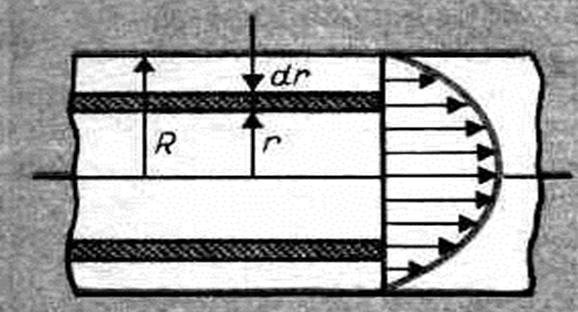
2. Метод Пуазейля. Этот метод основан на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l. В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr (рис. 54).
Сила внутреннего трения, действующая на боковую поверхность этого слоя,
где dS — боковая поверхность цилиндрического слоя; знак минус означает, что при возрастании радиуса скорость уменьшается. Для установившегося течения жидкости сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силой давления, действующей на его основание:
После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получим
Отсюда видно, что скорости частиц жидкости распределяются по параболическому закону, причем вершина параболы лежит на оси трубы.
откуда вязкость
14.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.105.194 (0.029 с.) |












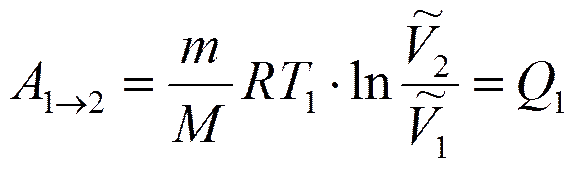













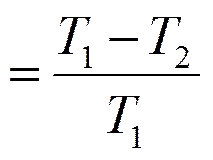



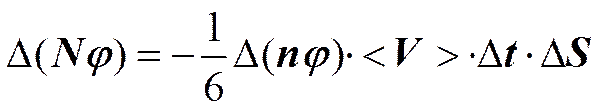

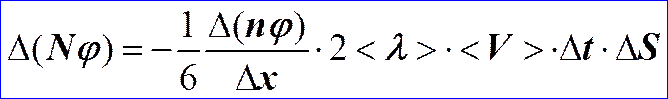 - основное уравнение явления переноса.
- основное уравнение явления переноса.
 - уравнение диффузии (уравнение Фика).
- уравнение диффузии (уравнение Фика). - градиент плотности.
- градиент плотности.
 ; (i – степень свободы, i = 3, 5,6)
; (i – степень свободы, i = 3, 5,6)






 - уравнение теплопроводности (уравнение Фурье).
- уравнение теплопроводности (уравнение Фурье). -
-

 =
= - уравнение трения (уравнение Ньютона).
- уравнение трения (уравнение Ньютона).

 — кинематическая вязкость;
— кинематическая вязкость;