
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное логарифмическое тождество ⇐ ПредыдущаяСтр 3 из 3
Логарифм произведения — это сумма логарифмов
Логарифм частного — это разность логарифмов
Свойства степени логарифмируемого числа и основания логарифма Показатель степени логарифмируемого числа Показатель степени основания логарифма
Переход к новому основанию
2) Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны. Теорема. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом. Док-во
Билет 15 1) Теорема 1. Функция ex дифференцируема в каждой точке области определения и (ex)`=ex.. Теорема 2. Показательная функция а x дифференцируема в каждой точке области определения и (ax)`=axlna. 2) Прямоугольная система координат в пространстве представляет собой 3 перпендикулярные прямые, имеющие направление (оси координат) и одну общую точку пересечения (координат). Абсцисса (х), ордината(у), аппликата(z) Билет 16 1) Первообразной для функции аx на R является функция Действительно, ln a — постоянная, и поэтому
при любом х. Этим доказано, что 2) Цили́ндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей. Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой
Билет 17 1) Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Простейшим логарифмическим уравнением является уравнение вида log a x = b. Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab.
Утверждение 2. Уравнение log a f (x) = log a g (x) (a > 0, a ≠ 1) равносильно одной из систем (очевидно, выбирается та система, неравенство которой решается проще)
Утверждение 3. Уравнение log h (x) f (x) = log h (x) g (x) равносильно одной из систем
Нужно подчеркнуть, что в процессе решения логарифмических уравнений часто используются преобразования, которые изменяют область допустимых значений (ОДЗ) исходного уравнения. Следовательно, могут появиться "чужие" решения или могут быть потеряны решения. Например, уравнения f (x) = g (x) и log a f (x) = log a g (x) или log a [ f (x)· g (x)] = b и log a f (x) + log a g (x) = b вообще говоря, неравносильны (ОДЗ уравнений справа уже). Следовательно, при решении логарифмических уравнений полезно использовать равносильные преобразования. В противном случае, проверка полученных решений является составной частью решения. Более того, необходимо учитывать и преобразования, которые могут привести к потере корней. 2) Сфе́ра — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии не больше заданного. (x-x0)2+(y-y0)2+(z-z0)2=R2 – Уравнение Теорема. Радиус сфера, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости Билет 18 1) Неравенство, содержащее неизвестное под знаком логарифма или (и) в его основании называется логарифмическим неравенством. В процессе решения логарифмических неравенств часто используются следующие утверждения относительно равносильности неравенств и учитываются свойства монотонности логарифмической функции. Утверждение 1. Если a > 1, то неравенство log a f (x) > log a g (x) равносильно системе неравенств
Утверждение 2. Если 0 < a < 1, то неравенство log a f (x) > log a g (x) равносильно системе неравенств
Утверждение 3. Неравенство log h (x) f (x) > log h (x) g (x) равносильно совокупности систем неравенств
Подчеркнем, что в неравенстве log a f (x) > log a g (x) вместо знака > может фигурировать любой из знаков ≥, <, ≤. В этом случае утверждения 1-3 соответственно преобразуются. 2) Теорема. Объём прямой призмы равен произведению площади основания на высоту Док-во: теорема для треугольной прямой призмы Рассмотрим прямую треугольную призму АВСА1В1С1 с объёмом V и высотой h. Проведём такую высоту треугольника АВС (отрезок BD), которая разделяет этот треугольник на два треугольника. Плоскость BB1DD1 разделяет данную призму на две призмы, основаниями которых являются прямоугольные треугольники АВD и BDC. Поэтому объёмы V1 и V2 этих призм соответственно равны SABD*h и SBCD*h. По свойству 2 объёмов V=V1+V2, т.е. V=SABD*h+SBCD*h=(SABD+SBCD)*h. Таким образом, V=SABC*h.
Док-во: теорему для произвольной прямой призмы с высотой h и площадью основания S. Такую призму можно разбить на прямые треугольные призмы с высотой h. Например, на рис., изображена пятиугольная призма, которая разбита на три прямоугольные призмы, Выразим объём каждой призмы по формуле V=SABC*h и сложим эти объёмы. Внося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т.е. площадь S основания исходной призмы. Таким образом объём исходной призмы равен произведению S*h. Билет 19 1) Производная функции y = ln x существует и выражается формулой На основании свойств логарифмов имеем
2) Теорема. Объём цилиндра равен произведению площади основания на высоту. Док-во: Впишем в данный цилиндр P радиуса r и высоту h правильную n-угольную призму Fn, а в эту призмы впишем цилиндр Pn. Обозначим через V и Vn объёмы цилиндров P и Pn, через rn радиус цилиндра Pn. Так как объём призмы Fn равен Sn*h, где Sn – площадь основания призмы, а цилиндр P содержит призмы Fn, которая в свою очередь содержит цилиндр Pn, то Vn<Sn*h<V. Будет неограниченно увеличивать число n. При этом радиус rn цилиндра Pn стремится к радиусу r цилиндра P (rn=cos180/n стремится к r при n ~). Поэтому объём цилиндра Pn стремится к объёму цилиндра P: lim n стремится к ~ Vn=V. Из неравенств Vn<Sn*h<V следует, что lim n стремится к ~ Sn*h=V. Но lim n стремится к ~ Sn=Пr2. Таким образом V=Пr2*h. Обозначив площадь Пr2 основания цилиндра буквой S, из формулы V=Пr2*h получим V=S*h. Билет 20 1) Если f(x) = xp, где p - действительное число, то 2) Теорема. Объём наклонной призмы равен произведению основания на высоту. Док-во: Для треугольной призмы: Рассмотрим треугольную призмы с объёмом V площадью основания S и высотой h. Отметим точку О на одном из оснований призмы и направим ось Ох перпендикулярно к основаниям. Рассмотрим сечение призмы плоскостью, перпендикулярной к оси Ох и, значит, параллельной плоскости основания. Обозначим буквой х абсциссу точки пресечения этой плоскости с осью Ох, а через S(x) – площадь получившегося сечения.
Докажем, что площадь S(x) равна площади S основания призмы. Для этого заметим, что треугольники АВС (основание призмы) и А1В1С1 (сечение призмы рассматриваемой плоскостью) равны. Четырёхугольник АА1В1В – параллелограмм (отрезки АА1 и ВВ1 равны и параллельны), поэтому А1В1=АВ. Аналогично доказывается, что В1С1=ВС и А1С1=АС. Треугольники А1В1С1 и АВС равны по трём сторонам. Следовательно, S(x)=S. Применяя теперь основную формулу для вычисления объёмов тел при а=0 и b=h, получаем V= h интеграл 0 S(x)dx= h интеграл 0 Sdx= S h интеграл 0 dx= S*h h|0=S*h Док-во: для произвольной призмы: Докажем теперь теорему для произвольной призмы с высотой h и площадью основания S. Такую призму можно разбить на треугольные призмы с общей высотой h. Выразим объём каждой треугольной призмы по доказанной нами формуле и сложим эти объёмы. Внося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т.е. площадью S основания исходной призмы. Таким образом, объём исходной призмы равен S*h.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.250.114 (0.017 с.) |



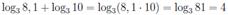




 , в частности если m = n, мы получаем формулу:
, в частности если m = n, мы получаем формулу:  , например:
, например: 
 , частности, если c = b, то
, частности, если c = b, то  , и тогда:
, и тогда:




 .
.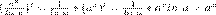
 есть первообразная для аx на R. А из равенства (еx)' = еx для всех х следует, что еx есть первообразная для еx на R.
есть первообразная для аx на R. А из равенства (еx)' = еx для всех х следует, что еx есть первообразная для еx на R. и длиной
и длиной  , равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:
, равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:



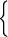
 (15). В случае сложной логарифмической функции y = ln u, где u – дифференцируемая функция аргумента x, формула (15) примет вид
(15). В случае сложной логарифмической функции y = ln u, где u – дифференцируемая функция аргумента x, формула (15) примет вид  (16). Пользуясь формулой (16), найдём производную логарифмической функции с произвольным положительным основанием a. Пусть
(16). Пользуясь формулой (16), найдём производную логарифмической функции с произвольным положительным основанием a. Пусть 
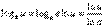 Так как
Так как  - постоянный множитель, то
- постоянный множитель, то или
или  .
. Если показатель степени является отрицательным числом, т.е. f(x) = x−p, то
Если показатель степени является отрицательным числом, т.е. f(x) = x−p, то


