Производство с двумя переменными факторами в долговременном периоде. Замещаемость факторов. Изокванты.

Рассмотрим вариант, когда переменными являются два фактора производства, которые при определенном сочетании дают в результате один объем производимого продукта. Возьмем, например, затраты труда и капитала при производстве обуви. Затраты труда обозначим за X, затраты капитала - через Y. При определенной комбинации этих двух факторов может быть произведено 200 пар обуви (Q = 200). Изменение капитала и труда может происходить в обратном направлении. При этом возрастание одного фактора и уменьшение другого происходят таким образом, что общий объем производства остается на прежнем уровне.

Эту зависимость можно представить графически с использованием изокванты (рис.66).

Изокванта, или кривая равного продукта, отражает все возможные комбинации двух факторов, которые могут быть использованы для производства определенного объема продукта. С увеличением объемов используемых переменных факторов, возникает возможность выпуска большего объема продукции. Изокванта, отражающая производство большего объема продукта, будет расположена правее и выше предыдущей изокванты.

Отрицательный наклон изоквант объясняется тем, что увеличение использования одного фактора при определенном объеме выпуска продукта всегда будет сопровождаться уменьшением количества другого фактора.

Возникает вопрос, на сколько нужно увеличить объем капитала (фактор y), чтобы уменьшить на одного человека применение живого труда (фактор x) при заданном объеме выпуска продукции? Чтобы ответить нужно рассмотреть крутизну наклона изокванты, который характеризуется предельной нормой технологического замещения (MRTS_x,y).

Предельная норма технологического замещения измеряется соотношением изменения фактора y к изменению фактора x. Поскольку замена факторов происходит в обратном отношении, то математическое выражение показателя MRTS_x,y берется со знаком минус: MRTS_x,y = - ^y/ _x

Если мы возьмем какую-либо точку на изокванте, например, точку A (рис.68) и проведем к ней касательную KM, то тангенс угла даст нам значение MRTS_x,y: MRTS_x,y = tg .

Можно отметить, что в верхней части изокванты угол будет достаточно велик, что говорит о том, что для изменения фактора x на единицу требуются значительные изменения фактора y. Следовательно, в этой части кривой значение MRTS_x,y будет велико.

По мере движения вниз по изокванте значение предельной нормы технологического замещения будет постепенно убывать. Это означает, что для увеличения фактора x на единицу потребуется незначительное уменьшение фактора y.

В реальных производственных процессах встречается два исключительных случая в конфигурации изоквант. Это ситуация, когда два переменных фактора идеально взаимозаменяемы, и случай, когда они жестко взаимодополняют друг друга. В первом случае (рис.70) при полной заменяемости факторов производства MRTS_x,y = const. Подобную ситуацию можно представить при возможности полной автоматизации производства. Тогда в точке A весь процесс производства будет состоять из затрат капитала. В точке B все машины будут заменены рабочими руками, а в точках C и D капитал и труд будут дополнять друг друга.

 

В ситуации с жесткой дополняемостью факторов (рис.71) предельная норма технологического замещения будет равна 0 (MRTS_x,y = 0). Если мы возьмем современный таксопарк с постоянным количеством машин (y₁), для работы на которых необходимо определенное количество водителей (x₁), то можно сказать, что количество обслуживаемых пассажиров в течение суток не увеличится, если мы увеличим численность водительского состава до x₂, x₃,... x_n. Объем производимого продукта увеличится с Q₁ до Q₂ только в том случае, если увеличится количество используемых машин в таксопарке и численность водителей.

 

 

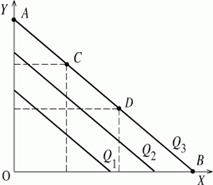
Бюджетное ограничение фирмы. Изокосты. Равновесие производителя.

Итак, изокванты позволяют производителю оценить возможности производства. А как насчет ограничений? Ведь на самом деле, ограничения производителя - это не только количества единиц экономических ресурсов, позволяющих произвести определенный объем производства, но и затраты на эти факторы производства. Помните, ведь производитель постоянно осуществляет перераспределение ресурсов, обеспечивающих один и тот же выпуск, так, чтобы предельные продукты разных факторов производства оказались равны друг другу. Когда-то мы определяли равновесие потребителя через точку оптимума - точку касания линии бюджетного ограничения и кривой безразличия. Продолжим аналогию и построим на нашем графике линию издержек для производителя: Пунктирная линия на графике - это затраты производителя на использование данных факторов производства. При таких издержках на производство фирма может себе позволить выпуск продукции, который представлен изоквантой Q2, а наиболее эффективной (оптимальной) комбинацией двух факторов производства (труда и капитала), будет та комбинация, которая представлена точкой касания линии издержек и изокванты, соответствующей объему выпуска продукции Q2. Как называется линия издержек производителя и как ее построить? Эта линия называется изокостой. Изокоста - линия, которая представляет все возможные сочетания факторов производства, суммарная стоимость которых одна и та же. Значит, равновесие производителя определяется точкой касания кривой, которая представляет различные комбинации факторов производства, дающих один и тот же выпуск продукции, и линии, представляющей сочетания тех же факторов производства, но с одним и тем же суммарным уровнем издержек на эти ресурсы - то есть их стоимостью. Положение изокосты определяется размером затрат на факторы производства: чем выше затраты, тем выше гра -фик изокосты. Так если изокванту мы обозначаем буквами Ql, Q2 и т.д. (это значит, что каждой изокванте соответствует определенный объем выпуска), то изокосту мы будем обозначать буквой С (cost), то есть CI, C2 и т.д. (это значит, что каждой изокосте соответствует определенный уровень издержек). Так же, как и для изокванты - объем выпуска, для изокосты можно рассчитать конкретное значение суммарной стоимости факторов производства. Запишем уравнение изокосты: То есть суммарная стоимость двух факторов производства равна сумме произведений их количества на стоимость (суммарная стоимость ресурсов А и В равна сумме единиц ресурса А с учетом его цены Р1 и единиц ресурса В с учетом его цены Р2). Так как мы с Вами говорим о двух факторах производства - труд и капитал, то можем записать уравнение изокосты в частном виде - то есть в том случае, когда ресурсом А является, например, капитал (К), а ресурсом В - труд (L). Что является стоимостью труда? Конечно, заработная плата. Значит, вместо величины А в уравнении изокосты, мы считаем количество труда, используемого в производстве (L), и издержки производителя на этот труд - ставка заработной платы (w, wage - заработная плата, англ.). Количество капитала, который затрачивается в данном процессе производства обозначается буквой К. Стоимость капитала будем выражать через ренту (процент от капитала), которую можно получить от его использования в производственном процессе (г, rent, рента, доход, англ.). Таким образом, мы получаем следующее уравнение изокосты: При помощиэтого уравнения можно выразить величину капитальных вложений через размер труда, прикладываемого в производстве, при заданном фиксированном уровне суммарных затрат. Когда изокоста касается графика кривой изокванты (и мы можем определить равновесную величину выпуска для производителя при данных издержках) - их наклоны совпадают. Наклон изкосты, как мы только что выяснили, определяется отношением ставки заработной платы к капитальным затратам. А наклон изокванты можно посчитать через величину предельной нормы технического замещения, то есть отношение изменения капитальных вложений к изменению трудового ресурса. Значит, если в точке равновесия совпадают наклоны изокосты и изокванты, значит, мы можем приравнять и отношения, которые им соответствуют, то есть:

Тема 5