
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Круговой процесс и его кпд. Обратимые и необратимые процессы. Цикл Карно. Первая и вторая теоремы Карно.
Отсюда видно, что КПД зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Для того, чтобы цикл Карно был обратимым, из него должна быть исключена передача теплоты при наличии разности температур (так как такие процессы необратимы в силу постулата Томсона). Значит, передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того, чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно. Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше чем КПД цикла Карно. Цикл Карно — идеальный термодинамический цикл. Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной системы не меняется. 1я теорема Карно: Пусть дан произвольный треугольник ABC. Тогда сумма алгебраических расстояний (англ.) от центра описанной окружности D до сторон треугольника ABC будет равна 2я теорема Карно: Пусть дан треугольник АВС и точки А1, В1, С1 на плоскости. Тогда перпендикуляры, опущенные из А1, В1, С1 на BC, АС, AВ соответственно, пересекаются в одной точке тогда и только тогда, когда Следствие 2й теоремы Карно: Перпендикуляры, опущенные из А1, В1, С1 на BC, АС, AВ соответственно, пересекаются в одной точке тогда и только тогда, когда перпендикуляры, опущенные из А, В, С на В1С1, А1С1, В1С1 соответственно, пересекаются в одной точке.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.30 (0.004 с.) |
 .
. , где r — радиус вписанной окружности, а R — описанной. Знак расстояния принимается отрицательным тогда и только тогда, когда отрезок DX (X = F, G, H) целиком лежит вне треугольника. В ее доказательстве используется теорема Птолемея.
, где r — радиус вписанной окружности, а R — описанной. Знак расстояния принимается отрицательным тогда и только тогда, когда отрезок DX (X = F, G, H) целиком лежит вне треугольника. В ее доказательстве используется теорема Птолемея.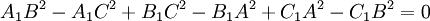 .
.


