
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учебные материалы по разделам ⇐ ПредыдущаяСтр 6 из 6
КУРСА ФИЗИКИ
I. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ. ОСНОВНЫЕ ФОРМУЛЫ · Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси X:
гдe · Проекция средней скорости на ось x
· Средняя путевая скорость
где Δ s — путь, пройденный точкой за интервал времени Δ t. Путь Δ s в отличие от разности координат Δ x = x2 — x1 не может убывать и принимать отрицательные значения, т. е. Δ s ³0 · Проекция мгновенной скорости на ось x
· Проекция среднего ускорение на ось x
· Проекция мгновенного ускорение на ось x
· Для прямолинейного движения законы изменения ускорения, скорости и перемещения имеют вид
· Кинематическое уравнение движения, материальной точки по окружности: φ = f(t), r = R = const. · Угловая скорость
· Угловое ускорение
· Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:
где · Полное ускорение:
· Угол между полным а и нормальным an ускорениями a = arсcos (an /a). · Для тел вращающихся с постоянным угловым ускорением (e = const)
· Кинематическое уравнение гармонических колебаний материальной точки x = A cos (ωt + φ), где х –смещение; А –амплитуда колебаний; ω – угловая или циклическая частота; φ – начальная фаза. · Скорость и ускорение материальной точки, совершающей гармонические колебания u a · Сила, действующая на колеблющуюся материальную точку массой m, равна · Полная энергия колеблющейся точки
· Период колебаний: а) тела, подвешенного на пружине
где m – масса тела, k – жесткость пружины; b) математического маятника
где l – длина маятника, g – ускорение свободного падения; с) физического маятника
где J – момент инерции колеблющегося тела относительно оси колебания, а - расстояние от оси колебания до центра тяжести маятника, · Сложение гармонических колебаний одного направления и одинаковой частоты а) амплитуда результирующего колебания
б) начальная фаза результирующего колебания
· Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях:
a) b) c)
· Импульс материальной точки массой m, движущейся со скоростью
· Второй закон Ньютона
где · Силы, рассматриваемые в механике: a) сила упругости
где k – коэффициент упругости (в случае пружины – жесткость), х – абсолютная деформация; b) сила тяжести;
c) сила гравитационного взаимодействия
где G – гравитационная постоянная; m 1 и m 2 – массы взаимо- действующих тел; r – расстояние между телами (тела рассмат- риваются как материальные точки); d) сила трения (скольжения)
где μ – коэффициент трения; N – сила нормального давления. · Закон сохранения импульса
или для двух тел (i = 2) m 1 где · Кинетическая энергия тела, движущегося поступательно
· Потенциальная энергия: a) упругодеформированной пружины
где k – жесткость пружины; х – абсолютная деформация;
b) тела, находящегося в однородном поле силы тяжести,
где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R – радиус Земли). · Закон сохранения механической энергии Е = Т + П = const. · Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки А = D Т = Т2 – Т1. · Основное уравнение динамики вращательного движения относительно неподвижной оси z M z = Jez, где М z – результирующий момент внешних сил относительно оси z, действующих на тело; ez – угловое ускорение относительно оси z; J – момент инерции относительно оси вращения. · Момент силы относительно оси вращения
где · По модулю момент силы равен
где α – угол между направлением силы и радиусом-вектором;
· Момент инерции некоторых тел массой m относительно оси z, проходящей через центр масс: a) стержня длиной l относительно оси, перпендикулярной стержню,
b) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),
где R – радиус обруча (полого цилиндра); c) диска (сплошного цилиндра) радиусом R относительно оси, перпендикулярной плоскости диска,
· Теорема Штейнера. Если известен момент инерции тела J0 относительно оси, проходящей через центр тяжести этого тела, то момент инерции J относительно любой другой оси, параллельной данной и отстоящей от нее на расстояние a, выражается формулой
где m – масса тела. · Момент импульса материальной точки относительно оси вращения L = mυR, · Момент импульса твердого тела относительно оси вращения
где mi – масса отдельной частицы;
· Закон сохранения момента импульса: а) в общем виде
где Li – момент импульса тела с номером i, входящего в состав системы; b) для двух тел
где J1, J2, ω1 , ω2 – моменты инерции и угловые скорости тел до взаимодействия, с) для одного тела, момент инерции которого может меняться J1ω1 = J2 ω2, где J1 и J2 – начальное и конечное значение моментов инерции, ω1 и ω2 – начальная и конечная угловые скорости тела. · Работа постоянного момента силы, действующего на враща -ющееся тело A = Mφ, где φ – угол поворота тела. · Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,
Примеры решения задач Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x = A+Bt+Ct3, где А = 2 м, В = 1 м/с, С =- 0,5 м/с3. Найти коорди- нату х, скорость uх и ускорение ах точки в момент времени t = 2 c.
Ускорение точки найдем, взяв первую производную от скорости по времени:
В момент времени t = 2 c
ux = (1 - 3×0,5×22) м/с = - 5 м/с; ах = 6× (-0,5)×2 м/с2 = - 6 м/с2. Пример 2. Тело вращается вокруг неподвижной оси по закону j = A+Bt+Ct2, где А = 10 рад, В = 20 рад/с, С = - 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0,1 м от оси вращения, для момента времени t = 4 c.
.Так как векторы
Подставляя выражения
Угловую скорость w найдем, взяв первую производную угла поворота по времени:
В момент времени t=2c модуль угловой скорости w = [ 20 + 2×(-2)×4 ] рад/с = 4 рад/с. Угловое ускорение найдем, взяв первую производную угловой скорости по времени:
Подставляя значения w, e и r в формулу (2), получаем
Пример 3.
Два шарика массами m1 и m2 движутся навстречу друг другу по идеально гладкой поверхности со скоростями
после взаимодействия. В проекциях:
Отсюда
Пример 4. Человек стоит на неподвижной тележке и бросает горизонтально камень массой m1 = 8 кг со скоростью u1 = 5 м/с. Определить, какую работу совершает человек, если масса человека вместе с тележкой равна m2 = 160 кг.
где u2 – скорость тележки с человеком сразу после броска.
По закону сохранения импульса m1u1 = m2u2, откуда
Следовательно,
Подставляя значения m1, m2, u1, u2 в формулу (3), найдем
Пример 5. Шар массой m1, движущийся горизонтально с некоторой скоростью u1, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
Как видно из формулы (1), для определения e надо найти
Решим совместно уравнения (2) и (3)
Подставив это выражение
Из найденного соотношения видно, что доля переданной энергии зависит только от массы сталкивающихся шаров.
Пример 6. Определить работу А внешней силы при растяжении двух пружин жесткостью k1 = 200 H/м и k2 = 350 H/м соединенных последовательно, если суммарное удлинение пружин Δ l = 4 см.
x = x1 + x2, (1) где x1 – удлинение первой пружины, x2 – удлинение второй пружины. Согласно закону Гука F1 = - k1 x1, и F2 = - k2 x2, откуда
Подставляя значение x1 и x2 в уравнение (1) получим:
При малой деформации dx работа внешней силы равна dA = F dx (3) Полную работу внешней силы при деформации пружины найдем проинтегрировав выражение (3) от от 0 до x0 ,учитывая при этом, что внешняя сила направлена в сторону противоположную силе Гука (Fвнеш. = -F);
Проверим размерность:
Убедившись, что полученная единица является единицей работы (Дж), подставим в формулу (4) значения величин и произведем вычисления:
Пример 7. При выстреле из пружинного пистолета вертикально вверх пуля массой m = 20 г поднялась на высоту h = 5 м. Определить жесткость k пружины пистолета, если она была сжата на х = 10 см. Массой пружины и силами трения пренебречь.
Согласно ему полная механическая энергия Е1 системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии Е2 в конечном состоянии (когда пуля поднялась на высоту h), т. е. Е1 = Е2, или Т1 + П1 = Т2 + П2, (1) где Т1, Т2, П1 и П2 – кинетические и потенциальные энергии системы в начальном и конечном состоянии. Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид П1 = П2. (2) Примем потенциальную энергию пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высоту подъема пули будем отсчитывать от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т. е. П1 = ½ kx2, а в конечном состоянии – потенциальной энергии пули на высоте h, т. е. П2 = mgh.
Подставив выражения П1 и П2 в формулу (2), найдем ½ kx2 = mgh, откуда k = 2mgh/x2. (3) Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим их единицы:
Убедившись, что полученная единица является единицей жесткости (1 Н/м), подставим в формулу (3) значения величин и произведем вычисления:
Пример 8. Через блок в виде сплошного диска, имеющего массу m =0,08 кг (рис. 3), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 =0,1 кг и m2 =0,2 кг. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
Для первого груза
для второго груза
Под действием моментов сил
(m2g – m2a) r – (m1g + m1a) r = m r2a / (2 r). После сокращения на r и перегруппировки членов найдем:
После подстановки числовых значений получим:
Пример 9. Маховик в виде сплошного диска радиусом R = 0,2 м и массой m = 50 кг раскручен до частоты вращения n1 = 480 об/мин и предоставлен сам себе. Под действием силы трения маховик остановился через t = 50 с. Найти момент M сил трения.
оси z, совпадающей с геометрической осью махо- вика, за интервал времени dt; случае момент сил трения), действующих на маховик относительно оси z. Момент сил трения можно считать не изменяющимся с течением времени (
При вращении твердого тела относительно неподвижной оси изменение проекции момента импульса
где Jz – момент инерции маховика относительно оси z; Приравнивая правые части равенства (2) и (3), получим
Момент инерции маховика в виде сплошного диска определяется по формуле
Изменение угловой скорости
Подставив в формулу (4) выражение Jz и
Проверим, дает ли расчетная формула единицу момента силы (Н·м). Для этого в правую часть формулы вместо символов величин подставим их единицы:
Подставим в (5) числовые значения величин и произведем вычисления, учитывая, что n1=480 об/мин = 8 об/с;
Знак минус показывает, что момент сил трения оказывает на маховик тормозящее действие.
Пример 10.
Платформа в виде сплошного диска радиусом R = 1,5 м и массой m1 = 180 кг вращается около вертикальной оси с частотой n=10 об/мин. В центре платформы стоит человек массой m2 = 60 кг. Какую линейную скорость v относительно пола помещения будет иметь человек, если он перейдет на край платформы?
где J – момент инерции платформы с человеком от- носительно оси z; Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии J=J1+J2, а в конечном состоянии С учетом этого, равенства (1) примет вид
где значения моментов инерции J1 и J2 платформы и человека соответственно относятся к начальному состоянию системы; Момент инерции платформы относительно оси z при перехо- де человека не изменяется: Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (
После сокращения на R2 и простых преобразований находим скорость: v = v =
Пример 11. Материальная точка массой m = 5 г совершает гармонические колебания с частотой v = 0,5 сек-1. Амплитуда колебаний А = 3 см. Определить: 1) скорость υ точки в момент времени, когда смещение x = 1,5 см; 2) максимальную силу Fмакс, действующую на точку; 3) полную энергию E колеблющейся точки.
Формулу скорости получим, взяв первую производную от смещения по времени,
Чтобы выразить скорость через смещение, надо исключить из (1) и (2) время. Для этого возведем оба уравнения в квадрат и сложим:
Решив последнее уравнение относительно υ, найдем
Подставив в это выражение числовые значения величин, получим:
Знак "плюс" соответствует случаю, когда направление скорости совпадает с положительным направлением оси x. Знак "минус "соответствует случаю, когда направление скорости совпадает с отрицательным направлением оси x.
2) Силу, действующую на точку, найдем по второму закону Ньютона:
где а – ускорение точки, которое получим, если возьмем производную по скорости от времени:
или
Подставив выражение для ускорение в (4), будем иметь:
Отсюда получим максимальное значение силы
Подставив в это уравнение числовые значения величин, найдем
3) Полная энергия колеблющейся точки есть сумма кинети- ческой и потенциальной энергий, вычисленных для любого момента времени. Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В это время потенциальная энергия равна нулю. Поэтому полная энергия Е колеблющейся точки равна максимальной кинетической энергии Тмакс и может быть определена по формуле
Максимальную скорость можно определить по формуле (2), если принять
Подставив это выражение скорости в (5), найдем
После подстановки числовых значений получим
Пример 12.
На концах тонкого стержня длиной l = 30 см и массой mст= 400 г укреплены грузики массой m1 = 200 г и m2 = 300 г. Стержень колеблется около горизонтальной оси, проходящей через его середину (рис. 4). Определить период Т колебаний, совершаемых стержнем.
Момент инерции физического
Общий момент инерции физического маятника равен
Вынеся за скобку множитель
Подставив в (4) числовые значения, получим
Масса физического маятника состоит из массы стержня и массы грузиков
Для определения расстояния а центра тяжести маятника от оси вращения напишем условие равновесия стержня с грузиками, находящегося в горизонтальном положении, относительно центра тяжести
Сократив это равенство на g и, решив его относительно а, получим
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.8.110 (0.213 с.) |
 .
. — некоторая функция времени.
— некоторая функция времени.
 =
=  .
. =
=  .
. .
. =
=  .
. .
.

 .
.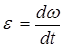 .
. = ωR, aτ = εR, an = ω2R,
= ωR, aτ = εR, an = ω2R,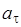 и an - модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε - модуль углового ускорения; R - радиус окружности.
и an - модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε - модуль углового ускорения; R - радиус окружности. .
.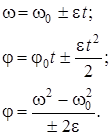
 - Aωsin (ωt +φ),
- Aωsin (ωt +φ), = - A ω2cos (ωt +φ).
= - A ω2cos (ωt +φ). .
.
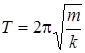 ,
, ,
, ,
, - приведенная длина физического маятника.
- приведенная длина физического маятника. ;
; .
.
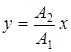 , если разность фаз
, если разность фаз  ;
; , если разность фаз
, если разность фаз  ;
; , если разность фаз
, если разность фаз  .
. ,
, .
.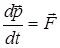 ,
, – результирующая сила, действующая на материальную точку.
– результирующая сила, действующая на материальную точку. ,
, ;
; ,
, ,
, ,
, + m 2
+ m 2  = m 1
= m 1  + m 2
+ m 2  ,
, или
или  .
. ,
, ,
, ,
, - радиус-вектор, связывающий ось вращения с точкой приложения внешней силы
- радиус-вектор, связывающий ось вращения с точкой приложения внешней силы  ,
,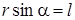 - кратчайшее расстояние между линией действия силы и осью вращения и называется плечом силы.
- кратчайшее расстояние между линией действия силы и осью вращения и называется плечом силы. ;
; ,
, .
. ,
, ,
, - ее скорость; ri – расстояние от оси вращения до частицы.
- ее скорость; ri – расстояние от оси вращения до частицы. ,
, ,
, - те же величины после взаимодействия;
- те же величины после взаимодействия; , или
, или  .
. .
. .
. , движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения
, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения  , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения  , направленного к центру кривизны траектории (рис. 1):
, направленного к центру кривизны траектории (рис. 1): 

 . (1)
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами
. (1)
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами
 ,
где w – модуль угловой скорости тела; e – модуль его углового ускорения.
,
где w – модуль угловой скорости тела; e – модуль его углового ускорения.
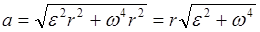 . (2)
. (2) .
. рад/с2.
рад/с2. .
. ,
где
,
где  - импульс шариков до столкновения;
- импульс шариков до столкновения;  – импульс
– импульс
 -?
-?






 .
. .
. , (1)
, (1)
 . (2)
. (2) . (3)
. (3) .
. , (1)
где
, (1)
где  и Т1 – скорость и кинетическая энергия первого шара до удара;
и Т1 – скорость и кинетическая энергия первого шара до удара;  и Т2 – скорость и кинетическая энергия второго шара после удара.
и Т2 – скорость и кинетическая энергия второго шара после удара.
 ; (2)
; (2) . (3)
. (3) .
. .
.
 (2)
(2) . (4)
. (4) .
. .
. .
.
 ; (1)
; (1) . (2)
. (2) и
и  относительно оси z, перпен- дикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению
относительно оси z, перпен- дикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению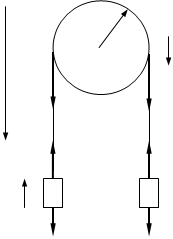 r
x
r
x
 m1 g m2 g
Рис. 3
m1 g m2 g
Рис. 3
 , (3)
где
, (3)
где  – момент инерции блока относительно оси вращения.
Согласно третьему закону Нью-
тона, с учетом невесомости нити
– момент инерции блока относительно оси вращения.
Согласно третьему закону Нью-
тона, с учетом невесомости нити  (4)
(4) .
. , (1)
где
, (1)
где  - изменение проекции на ось z момента импульса маховика, вращающегося относительно
- изменение проекции на ось z момента импульса маховика, вращающегося относительно
 - момент внешних сил (в данном
- момент внешних сил (в данном , (2)
, (2)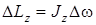 , (3)
, (3) - изменение угловой скорости маховика.
- изменение угловой скорости маховика.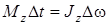 , откуда
, откуда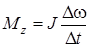 . (4)
. (4) .
. выразим через конечную n2 и начальную n1 частоты вращения, пользуясь соотношением
выразим через конечную n2 и начальную n1 частоты вращения, пользуясь соотношением 
 .
. . (5)
. (5)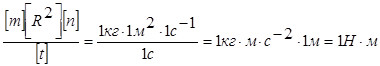 .
.
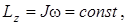 (1)
(1)
 - угловая скорость платформы.
- угловая скорость платформы.
 (2)
(2)
 - к конечному.
- к конечному. Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J2 в начальном состоянии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека
Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J2 в начальном состоянии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека 
 v/R, где v – скорость человека относительно пола):
v/R, где v – скорость человека относительно пола): v/R.
v/R. .
. м/с = 1 м/с.
м/с = 1 м/с. (2)
(2) .
. (3)
(3)
 , (4)
, (4)



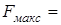


 (5)
(5)



 , (1)
где J – момент инерции маятника, m – масса маятника, а – расстояние от центра тяжести (центра масс) маятника до оси.
, (1)
где J – момент инерции маятника, m – масса маятника, а – расстояние от центра тяжести (центра масс) маятника до оси.
 J1 и J2 обоих грузиков и момента инерции J3 стержня
J1 и J2 обоих грузиков и момента инерции J3 стержня
 Пренебрегая размерами грузиков, получим
Пренебрегая размерами грузиков, получим
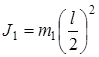 и
и  .
Момент инерции стержня относитель- но оси, проходящей через его середи- ну, определяется по формуле
.
Момент инерции стержня относитель- но оси, проходящей через его середи- ну, определяется по формуле


 , получим
, получим (2)
(2)





